lập phương trình đường thẳng đi qua điểm A(-2,1)và // vs góc phần tư phân giác của góc phần tư thứ 2
Viết pt tổng quát của đường thẳng d
a) Đi qua điểm M(-2;-5) và song song với đường phân giác góc phần tư thứ nhất
b) Đi qua điểm M(3;-1) và vuông góc với đường phân giác góc phần tư thứ hai
c) Viết pt tham số của đg thẳng d đi qua điểm M(-4;0) và vuông góc với đường phân giác thứ hai
a, Đường phân giác góc phần tư thứ nhất là một nửa đường thẳng x - y = 0 nằm ở góc phần tư thứ nhất
=> d nhận (1 ; -1) làm vecto pháp tuyến
=> PT đi qua M (-2 ; -5) là
x + 2 - y - 5 = 0 ⇔ x - y - 3 = 0
b, c, Lười lắm ko làm đâu :)
Viết phương trình tham số của đường thẳng d đi qua điểm M(-3;5) và song song với đường phân giác của góc phần tư thứ nhất
Đường phân giác của góc phần tư thứ nhất có 1 vtcp là (1;1)
\(\Rightarrow\) d cũng nhận (1;1) là 1 vtcp
Phương trình: \(\left\{{}\begin{matrix}x=-3+t\\y=5+t\end{matrix}\right.\)
Trong mặt phẳng Oxy,viết phương trình tổng quát của:
a)đường thẳng Ox
b)đường thẳng Oy
c)đường phân giác của góc phần tư thứ nhất
a. Đường thẳng Ox nhận \(\left(0;1\right)\) là 1 vtpt và đi qua O(0;0) nên có pt:
\(0\left(x-0\right)+1\left(y-0\right)=0\Leftrightarrow y=0\)
b. Đường thẳng Oy nhận (1;0) là 1 vtpt và đi qua O nên có pt:
\(1\left(x-0\right)+0\left(y-0\right)=0\Leftrightarrow x=0\)
c. Gọi \(M\left(x;y\right)\) với \(x;y>0\) là 1 điểm bất kì nằm trên phân giác góc phần tư thứ nhất
\(\Rightarrow d\left(M;Ox\right)=d\left(M;Oy\right)\Leftrightarrow\dfrac{\left|x\right|}{\sqrt{1^2+0^2}}=\dfrac{\left|y\right|}{\sqrt{1^2+0^2}}\Leftrightarrow x-y=0\)
Làm tương tự như bài 50 đối với đường phân giác của các góc phần tư thứ II; IV.
Tức là:
Vẽ một hệ trục toạ độ và đường phân giác của các góc phần tư thứ II,IV.
Đánh dấu điểm A nằm trên đường phân giác đó và có hoành độ là 2. Điểm A có tung độ là bao nhiêu?
Hình vẽ:
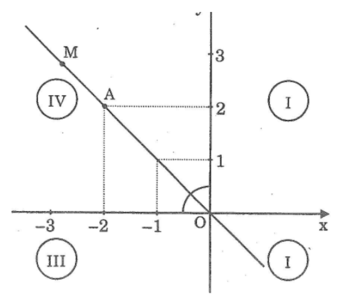
Điểm A có hoành độ bằng 2 thì điểm A có tung độ bằng - 2.
xác định hàm số y=ax+b
a) đths đi qua điểm A(2;1) và có hệ số góc bằng căn 3
b) đths đi qua điểm A(2;1) và song song với đường phân giác của góc phần tư thứ hai
Cho hai số phức α = a + bi, β = c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ: Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba
trên mặt phẳng tọa độ Oxy vẽ đường thẳng d chứa tia phân giác của các góc phần tư thứ I và góc phần tư thứ III. hỏi đường thẳng d là đồ thị hàm số nào?
Tìm m để đồ thị hàm số y=(m-1)x+2n-3 song song với đường phân giác góc phần tư thứ nhất thứ ba và đi qua điểm A(1;2)
Cho ba đường thẳng d1: y = 2x + 8; d2: y = mx – 2m + 3; d3: y = x + 2.
1. Tìm m để d2 đi qua điểm E(1 ; 3).
2. Tìm m để d2 vuông góc với đường phân giác góc phần tư thứ hai.
3. Tìm m để ba đường thẳng trên đồng quy.
4. Tìm điểm cố định mà d2 luôn đi qua với mọi m. Từ đó tìm m để khoảng cách từ gốc O đến d2 là lớn
nhất.
5. Gọi d3 cắt 0x, 0y lần lượt tại A và B. Tìm A và B sau đó tính diện tích tam giác OAB theo hệ thức
lượng.
6. Lập phương trình đường thẳng d đi qua điểm M(3 ; 8) và song song với d3, cắt hai trục tọa độ tại C và
D. Tính độ dài đường cao của tam giác COD, từ đó suy ra khoảng cách từ điểm M đến d3.
7. Lập phương trình đường thẳng d’ qua M và vuông góc với d3. Tìm hình chiếu N của M trên d3, từ đó
tính khoảng cách từ M đến d3
1:Thay x=1 và y=3 vào (d2), ta được:
\(m-2m+3=3\)
hay m=0