Lương của các công nhân một nhà máy được cho trong bảng sau:

a) Nêu các nhóm số liệu và tần số. Giải thích ý nghĩa cho một nhóm số liệu và tẩn số của nó.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê trên.
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Cho các số liệu thống kê được ghi trong hai bảng sau
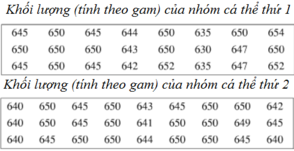
a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là:
[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
c) Biểu đồ tần suất hình cột:
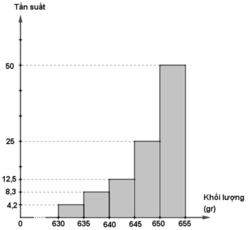
- Đường gấp khúc tần suất
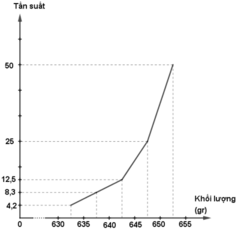
d) Biểu đồ tần số
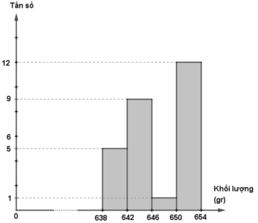
- Đường gấp khúc tần số
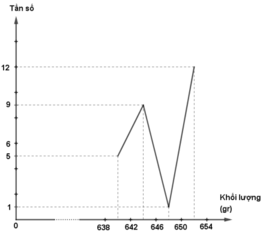
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
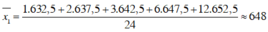
- Phương sai:
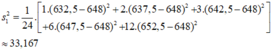
- Độ lệch chuẩn:
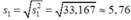
* Xét bảng phân bố ở câu b):
- Số trung bình:
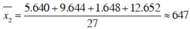
- Phương sai:
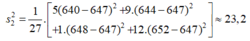
- Độ lệch chuẩn:
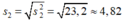
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:

a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Tham khảo:
a)

b) Cỡ mẫu \(n = 60\)
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{15}} + {x_{16}}}}{2}\). Do \({x_{15}},\;{x_{16}}\) đều thuộc nhóm \(\left[ {40;50} \right)\) nên nhóm náy chứa \({Q_1}\). Do đó,
\(p = 5;\;\;{a_5} = 40;\;\;{m_5} = 15;\;\;{m_1} + {m_2} + {m_3} + {m_4} = 1 + 2 + 4 + 6 = 13;\;{a_6} - {a_5} = 10\)
Ta có \({Q_1} = 40 + \frac{{\frac{{60}}{4} - 13}}{{15}} \times 10 = 41,33\)
Ý nghĩa: Có 25% số giá trị nhỏ hơn 41,33
Tứ phân vị thứ hai, \({M_e}\) là \(\frac{{{x_{30}} + {x_{31}}}}{2}\). Do \({x_{30}};\;{x_{31}}\) đều thuộc nhóm \(\left[ {50;60} \right)\) nên nhóm này chứa \({M_e}\). Do đó,
\(p = 6;\;\;{a_6} = 50;\;\;{m_6} = 12;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} = 1 + 2 + 4 + 6 + 15 = 13;\;{a_7} - {a_6} = 10\)
Ta có: \({Q_2} = 50 + \frac{{\frac{{60}}{2} - 28}}{{12}} \times 10 = 51,66\)
Ý nghĩa: Có 50% số giá trị nhỏ hơn 51,66
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{45}} + {x_{46}}}}{2}\). Do \({x_{45}},\;{x_{46}}\) đều thuộc nhóm \(\left[ {60;70} \right)\) nên nhóm náy chứa \({Q_3}\). Do đó,
\(p = 7;\;\;{a_7} = 60;\;\;{m_7} = 10;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6} = 1 + 2 + 4 + 6 + 15 + 12 = 40; {a_8} - {a_7} = 10\).
Ta có: \({Q_3} = 60 + \frac{{\frac{{60 \times 3}}{4} - 40}}{{10}} \times 10 = 65\)
Ý nghĩa: Có 75% số giá trị nhỏ hơn 65.
Cho các số liệu thống kê được ghi trong hai bảng sau đây :
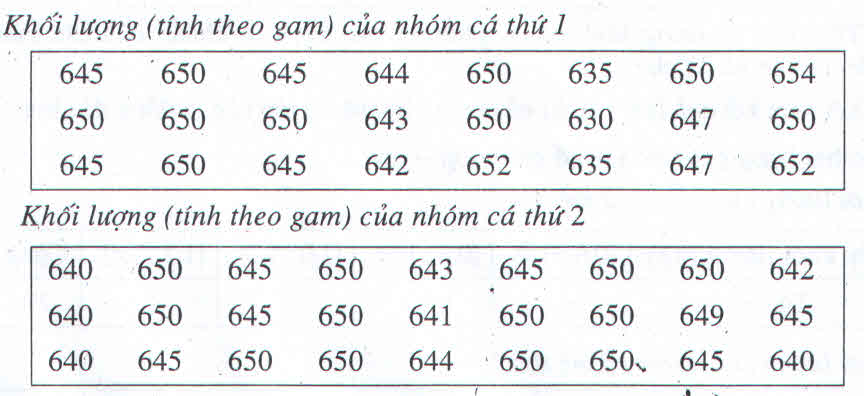
a. Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là :
[630;635); [635;640); [640;645); [645;650); [650;655]
b. Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là :
[638;642); [642;646); [646;650); [650;654]
c. Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất ?
d. Mô tả bảng phân bố tần số ghép lớp đã được lập ở câu b), bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e. Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố tần số và tần suất ghép lớp đã lập được
Từ đó, xem xét nhóm cá nào có khối lượng đồng đều hơn ?
a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
c) Biểu đồ tần suất hình cột:
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng): 
a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right) = \frac{1}{2}\left( {8,9 + 9,2} \right) = 9,05\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right) = \frac{1}{2}\left( {10,7 + 10,9} \right) = 10,8\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right) = \frac{1}{2}\left( {12,2 + 12,5} \right) = 12,35\)
b)

c) Tổng số nhân viên văn phòng là: \(n = 3 + 6 + 8 + 7 = 24\).
Gọi \({x_1};{x_2};...;{x_{24}}\) là lương tháng của các nhân viên văn phòng được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2},{x_3} \in \begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array};{x_4},...,{x_9} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array};{x_{10}},...,{x_{17}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array};{x_{18}},...,{x_{24}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right)\)
Ta có: \(n = 24;{n_m} = 8;C = 3 + 6 = 9;{u_m} = 10;{u_{m + 1}} = 12\)
Do \({x_{13}},{x_{14}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10 + \frac{{\frac{{24}}{2} - 9}}{8}.\left( {12 - 10} \right) = 10,75\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right)\).
Ta có: \(n = 24;{n_m} = 6;C = 3;{u_m} = 8;{u_{m + 1}} = 10\)
Do \({x_6},{x_7} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{24}}{4} - 3}}{6}.\left( {10 - 8} \right) = 9\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right)\).
Ta có: \(n = 24;{n_j} = 7;C = 3 + 6 + 8 = 17;{u_j} = 12;{u_{j + 1}} = 14\)
Do \({x_{18}},{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 12 + \frac{{\frac{{3.24}}{4} - 17}}{7}.\left( {14 - 12} \right) \approx 12,3\)
Cho các số liệu thống kê ghi trong bảng sau:
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân (đơn vị: phút)

Hãy lập bảng phân bố tần số, bảng phân bố tần suất
Bảng phân bố tần số
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 50 | 54 | cộng |
| Tần số | 4 | 5 | 20 | 10 | 8 | 3 | 50 |
Bảng phân bố tần suất
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 20 | 54 | Cộng |
| Tần suất (%) | 8 | 10 | 40 | 20 | 16 | 6 | 100% |
Cho các số liệu thống kê được ghi trong bảng sau
Mức lương hàng năm của các cán bộ và nhân viên trong một công ty (đơn vị nghìn đồng)
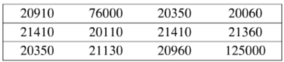
Tìm mức lương bình quân của các cán bộ và nhân viên trong công ti, số trung vị của các số liệu thống kê đã cho.
Nêu ý nghĩa của số trung vị
- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
- Số trung bình:
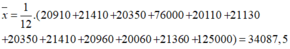
Sắp xếp các số liệu theo dãy tăng dần:
20060; 20110; 20350; 20350; 20910; 20960; 21130; 21360; 21410; 21410; 76000; 125000.
Số trung vị: Me = (20960 + 21130)/2 = 21045.
Ý nghĩa: Số trung vị đại diện cho mức lương trung bình của nhân viên (vì trong trường hợp này chênh lệch giữa các số liệu quá lớn nên không thể lấy mức lương bình quân làm giá trị đại diện).
Cho bảng số liệu:
DIỆN TÍCH GIEO TRỒNG PHÂN THEO NHÓM CÂY CỦA NƯỚC TA, NĂM 2005 VÀ NĂM 2016
(Đơn vị: nghìn ha)
Năm Các nhóm cây |
2005 |
2016 |
|
Tổng số |
13287,0 |
15112,1 |
|
Cây lương thực |
8383,4 |
8890,6 |
|
Cây công nghiệp |
2495,1 |
2978,9 |
|
Cây thực phẩm, cây ăn quả, cây khác |
2408,5 |
3242,6 |
Theo bảng số liệu, để thể hiện quy mô và cơ cấu diện tích gieo trồng phân theo nhóm cây của nước ta, năm 2005 và năm 2016, dạng biểu đồ nào sau đây thích hợp nhất?
A. Cột.
B. Tròn.
C. Ô vuông.
D. Miền.
Đáp án B
Theo bảng số liệu, để thể hiện quy mô và cơ cấu diện tích gieo trồng phân theo nhóm cây của nước ta, năm 2005 và năm 2016, dạng biểu đồ tròn thích hợp nhất
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:

Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:

Quãng đường (km) từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:

a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là \(\left[ {0;5} \right)\). Tìm giá trị đại diện cho mỗi nhóm
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).