Giả sử hai số có tổng S = 5 và tích P = 6. Thực hiện các bước sau để lập phương trình bậc hai nhận hai số đó làm nghiệm.
a) Gọi một số là x. Tính số kia theo x.
b) Sử dụng kết quả câu a và giả thiết, hãy lập phương trình để tìm x.
Tính diện tích S của hình thang ABCD theo x bằng hai cách:
1) Tính theo công thức: S = BH x (BC + DA) : 2
2) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
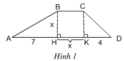
1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
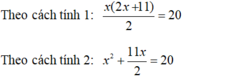
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Để thực hiện phép cộng \(\dfrac{5}{7} + \dfrac{{ - 3}}{4}\), em hãy làm theo các bước sau:
+ Quy đồng mẫu hai phân số \(\dfrac{5}{7}\) và \(\dfrac{{ - 3}}{4}\)
+ Sử dụng quy tắc cộng hai phân số cùng mẫu để tính tổng hai phân số sau khi đã quy đồng.
Ta có: \(\dfrac{5}{7} = \dfrac{{5.4}}{{7.4}} = \dfrac{{20}}{{28}}\) và \(\dfrac{{ - 3}}{4} = \dfrac{{ - 3.7}}{{4.7}} = \dfrac{{ - 21}}{{28}}\)
Như vậy, \(\dfrac{{20}}{{28}} + \dfrac{{ - 21}}{{28}} = \dfrac{{20 + \left( { - 21} \right)}}{{28}} = \dfrac{-1}{{28}}\)
Bài 6. Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau: Bước 1. x x + y Bước 2. y x - y Bước 3. x x – y
Bài 7: Xây dựng thuật toán để giải bài toán: Cho trước ba số dương a, b, c. Hãy cho biết 3 số đó có phải là độ dài ba cạnh của một tam giác hay không? Bài 8. Tìm hiểu ví dụ 6 mục 4 bài 5. Viết lại thuật toán tìm giá trị lớn nhất và nhỏ nhất của dãy số a1,a2,a3…. an cho trước.
Bài 7:
#include <bits/stdc++.h>
using namespace std;
double a,b,c;
int main()
{
cin>>a>>b>>c;
if ((a+b>c) && (a+c>b) && (b+c>a)) cout<<"Day la ba canh trong mot tam giac";
else cout<<"Day khong la ba canh trong mot tam giac";
return 0;
}
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c = 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau:
Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu.
Bước 2: Với điều kiện a, c trái dấu ta có a.c > 0 suy ra Δ = b2 - 4ac > 0.
Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.
Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu.
Lập luận trên sai từ bước nào?
A. Bước 1
B. Bước 2
C. Bước 3
D. Bước 4.
Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.
Tính diện tích S của hình thang ABCD (h.1) theo x bằng hai cách :
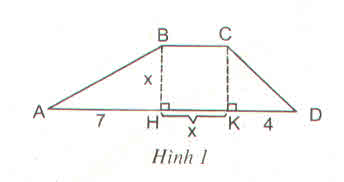
1) Theo công thức \(S=BH.\left(BC+DA\right):2\)
2) \(S=S_{ABH}+S_{BCKH}+S_{CKD}\)
Sau đó sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không ?
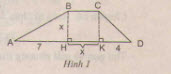
Hướng dẫn giải:
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S =
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S =
2) Ta có: S = SABH + SBCKH + SCKD.
= .AH.BH + BH.HK + CK.KD
= .7x + x.x + x.4
= x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
= 20 (1)
x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.
1. Hai vòi nước cùng chảy vào một cái bể cạn thì sau 10 giờ. Người ta mở vòi thứ nhất chảy trong 6 giờ thì được 1/2 bể. Sau đó, người ta khoá vòi thứ nhất và mở vòi thứ hai. Thời gian vòi thứ hai tiếp tục chảy đến khi đầy bể là? ( Làm cách tìm x. VD: Gọi số đó là x)
2. Khi thực hiện phép cộng hai số thập phân, Hương đã viết nhầm dấu phẩy của một số hạng sang bên phải một chữ số, do đó dẫn đến kết quả sai là 2490,78. Biết tổng đúng là 542,1. Vậy hiệu của hai số ban đầu ( Làm bằng cách tìm x. VD: Gọi số đó là x)
3. Một bể cá hình lập phương có cạnh 25cm đã sử dụng 60% thể tích bể để chứa nước. Một lượng nước bị bốc hơi làm mực nước trong bể giảm đi 70mm. Thể tích lượng nước còn lại trong bể là? ( Làm bằng cách tìm x. VD: Gọi số đó là x)
Giả sử cần viết chương trình nhập một số tự nhiên vào máy tính và in ra màn hình kết quả số đã nhập chẵn hay lẻ, chẳng hạn “5 là số lẻ”, “8 là số chẵn”. Hãy mô tả các bước của thuật toán để giải quyết bài toán trên và viết chương trình Python để thực hiện thuật toán đó. Mấy bạn ơi giúp mình với mình cần gấp lắm
Giả sử cần viết chương trình nhập một số tự nhiên vào máy tính và in ra màn hình kết quả số đã nhập chẵn hay lẻ, chẳng hạn “5 là số lẻ”, “8 là số chẵn”. Hãy mô tả các bước của thuật toán để giải quyết bài toán trên và viết chương trình Pascal để thực hiện thuật toán đó.
#include <bits/stdc++.h>
using namespace std;
long long a;
int main()
{
cin>>a;
if (a%2==0) cout<<"La so chan";
else cout<<"La so le";
return 0;
}
- Thuật toán chương trình:
Bước 1: Nhập một số tự nhiên n và một biến d;
Bước 2: Gán giá d=n mod 2;
Bước 3: Nếu d=0 thì đấy là số chẵn, ngược lại thì đấy là số lẻ;
Bước 4. Kết thúc thuật toán;
- Chương trình Pascal:

- Kết quả:
Phương pháp lai và phan tích cơ thể lai của Menđen gồm các bước:
(1) Đưa gải thuyết giải thích kết quả và chứng minh giả thuyết.
(2) Lai các dòng thuần khác nhau về một hoặc vào tính trạng rồi phân tích kết quả ở F1, F2, F3.
(3) Tạo các dòng thuần chủng.
(4) Sử dụng toán xác suất để phân tích kết quả lai.
Trình tự đúng của các bước mà Menđen đã thực hiện là:
A. (2) → (3) → (4) → (1)
B. (1) → (2) → (4) → (3)
C. (3) → (2) → (4) → (1)
D. (1) → (2) → (3) → (4)
Giả sử đã cho \({\log _a}M\) và ta muốn tính \({\log _b}M.\) Để tìm mối liên hệ giữa \({\log _a}M\) và \({\log _b}M,\) hãy thực hiện các yêu cầu sau:
a) Đặt \(y = {\log _a}M,\) tính M theo y;
b) Lấy loogarit theo cơ số b cả hai vế của kết quả nhận được trong câu a, từ đó suy ra công thức mới để tính y.
a) \(y = {\log _a}M \Leftrightarrow M = {a^y}\)
b) Lấy loogarit theo cơ số b cả hai vế của \(M = {a^y}\) ta được
\({\log _b}M = {\log _b}{a^y} \Leftrightarrow {\log _b}M = y{\log _b}a \Leftrightarrow y = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\)