Hình 5.37 cho thấy hình ảnh của những đường tròn qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và cặp đường tròn không giao nhau.

Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
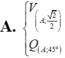
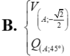
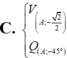
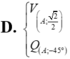
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
A. V A ; 2 2 Q A ; 45 °
B. V A ; − 2 2 Q A ; 45 °
C. V A ; − 2 2 Q A ; − 45 °
D. V A ; 2 2 Q A ; − 45 °
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
A. V A ; 2 2 Q A , 45 °
B. V A ; - 2 2 Q A , 45 °
C. V A ; - 2 2 Q A , - 45 °
D. V A ; 2 2 Q A , - 45 °
D
Đáp án A.
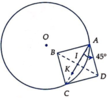
V A ; 2 2 A = K ⇒ K nằm giữa AC và AK = AD
Từ hình vẽ Q A ; 45 ° ( K ) = D
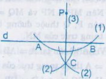
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
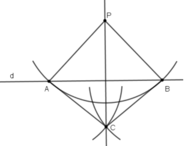
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
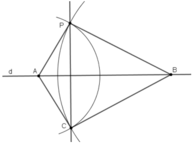
QUẢNG CÁOb) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.
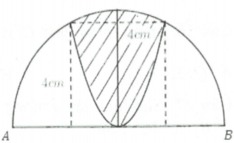
Cho nửa đường tròn đường kính AB = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 5 800 5 - 928 c m 3
B. V = π 15 800 5 - 928 c m 3
C. V = π 3 800 5 - 928 c m 3
D. V = π 15 800 5 - 464 c m 3
Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
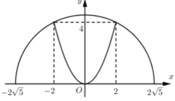
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 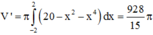
=> Thể tích cần tính 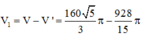
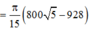
Cho nửa đường tròn đường kính A B = 4 5 . Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4 cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4 cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
A. V = π 15 800 5 - 464 c m 3
B. V = π 3 800 5 - 928 c m 3
C. V = π 5 800 5 - 928 c m 3
D. V = π 15 800 5 - 928 c m 3
vẽ một hình tròn có bán kính 2 cm. Trong hình tròn có 2 đường thẳng giao nhau tại tâm đường tròn O, P, Q,E ĐƯỜNG THẲNG 1. Đường thẳng đi qua 2 điểm . 2 đường thẳng nào cắt nhau. chỉ ra các điểm ko thẳng hàng
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.
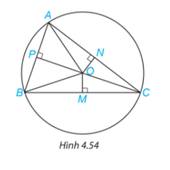
Vì A, B, C nằm trên đường tròn tâm O nên OA = OB = OC.
Xét hai tam giác ONA vuông tại N và ONC vuông tại N có:
OA = OC (cmt)
ON chung
Do đó ΔONA=ΔONC (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OMB vuông tại M và OMC vuông tại M có:
OB = OC (cmt)
OM chung
Do đó ΔOMB=ΔOMC (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OPA vuông tại P và OPB vuông tại P có:
OA = OB (cmt)
OP chung
Do đó ΔOPA=ΔOPB (cạnh huyền – cạnh góc vuông).
hình tròn thứ nhất có đường kính bằng bán kính hình tròn thứ hai.Tìm tỉ số phần trăm điện tích của hình tròn thứ nhất và hình tròn thứ hai
trình bày hẳn ra với ạ
em cần gấp![]()
Đề bài cho thế thì bảo cô giáo làm cho
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai