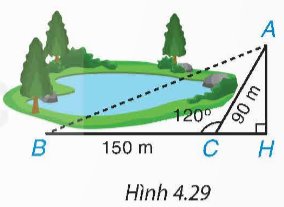
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và \(\widehat{ACB}\) = 120° (H.4.29). Hãy tính AB giúp bạn.
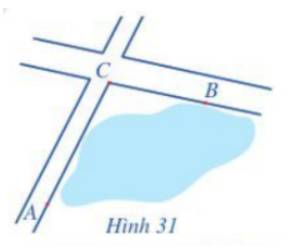
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.
Một ca nô xuôi dòng từ bến A đến bến B mất 8 giờ và ngược dòng từ bến B về bến A mất 10 giờ. Tính khoảng cách giữa hai điểm A và B, biết rằng vận tốc của dòng nước là 4km/h.
Gọi vận tốc cano khi nước lặng là x (km/h) với x>4
Vận tốc cano khi xuôi dòng: \(x+4\) (km/h)
Vận tốc cano khi ngược dòng: \(x-4\) (km/h)
Quãng đường cano xuôi dòng: \(8\left(x+4\right)\)
Quãng đường cano ngược dòng: \(10\left(x-4\right)\)
Do quãng đường xuôi dòng và ngược dòng như nhau nên ta có pt:
\(8\left(x+4\right)=10\left(x-4\right)\)
\(\Leftrightarrow2x=72\Rightarrow x=36\) (km/h)
Khoảng cách AB là: \(8\left(36+4\right)=320\left(km\right)\)
Một ca nô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai điểm A và B, biết rằng vận tốc của dòng nước là 2km/h.
Gọi x là khoảng cách từ A đến B
ta có : Hiệu vận tốc xuôi dòng và ngược dòng gấp 2 lần vận tốc dòng nước, hay ta có :
\(\frac{x}{4}-\frac{x}{5}=2\times2\) hay \(\frac{x}{20}=4\Leftrightarrow x=80km\)
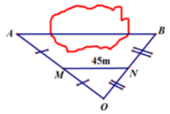
Để đo khoảng cách giữa hai địa điểm A, B bị ngăn cách bởi một hồ nước người ta đóng các cọc tại các vị trí A,B,M,N,O như hình vẽ và đo được MN=45m. Tính khoảng cách AB biết M,N lần lượt là trung điểm của OA,OB.
Bạn H đo đc khoảng cách từ vị trí mik đứng ( điểm K )đến cây D và cây E ở 2 bên hồ nước là KD=18m và KE=20,25m để tính đọ dài DE, H xác định điểm A nằm giữa K và D và điểm B nằm giữa K,E sao cho KA=6,4m,KB=7,2m và đo khoảng cách giữa A và B là AB = 32m
Chứng minh KB/KE =AK/AD
Chứng minh AB// DE
Tính khoảng cách giữa D và E
a: Sửa đề: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
\(\dfrac{KB}{KE}=\dfrac{7.2}{20.25}=\dfrac{16}{45}\)
\(\dfrac{KA}{KD}=\dfrac{6.4}{18}=\dfrac{16}{45}\)
Do đó: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
b: Xét ΔKDE có \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
nên AB//DE
c: Xét ΔKDE có AB//DE
nên \(\dfrac{AB}{DE}=\dfrac{KB}{KE}\)
=>\(\dfrac{32}{DE}=\dfrac{16}{45}=\dfrac{32}{90}\)
=>DE=90(m)
Bạn H đo đc khoảng cách từ vị trí mik đứng ( điểm K )đến cây D và cây E ở 2 bên hồ nước là KD=18m và KE=20,25m để tính đọ dài DE, H xác định điểm A nằm giữa K và D và điểm B nằm giữa K,E sao cho KA=6,4m,KB=7,2m và đo khoảng cách giữa A và B là AB = 32m
Chứng minh KB/KE =AK/AD
Chứng minh AB// DE
Tính khoảng cách giữa D và E
Một hồ nước nằm ở góc tạo bởi hai con đường (hình vẽ). Biết rằng khoảng cách từ A đến B bằng 7km, khoảng cách từ A đến C là 5km, B A C ^ = 120 ∘ Bốn bạn An, Cường, Trí, Đức dự đoạn khoảng cách từ B đến C như sau: An: 11km Cường: 10km Trí: 10,5km Đức: 9,5km.
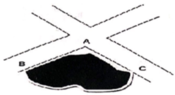
Hỏi dự đoán của bạn nào sát thực tế nhất?
A. Đức.
B. An.
C. Trí.
D. Cường.
Cùng một lúc,một ô tô đi từ A và một xe máy đi từ B ngược chiều nhau để đến điểm C ở giữa a và B. Địa điểm C cách A 165 km và cách B 134 km.Vận tốc của ô tô là 54 km/h của xe máy là 36 km/h.Hỏi a) xe nào đến C trước b) sau mấy h khoảng cách giữa hai xe rút ngắn còn 83 km
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc \({70^o}\) (Hình 5).
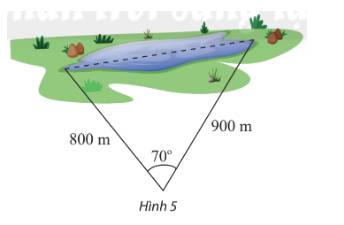
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
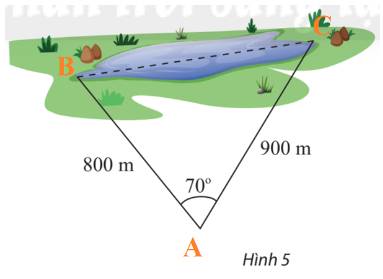
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\) Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
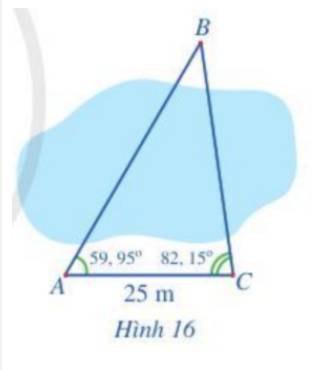
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.