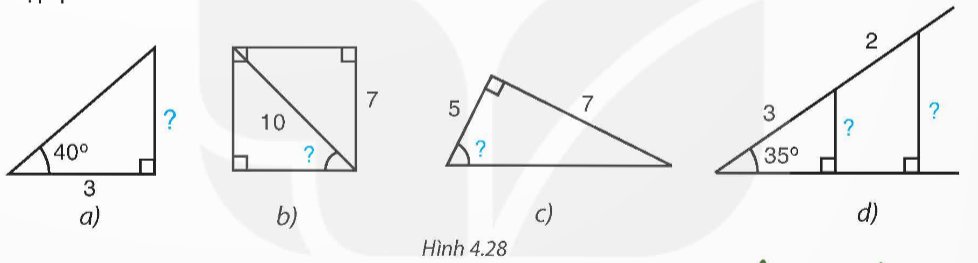
Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
Giải tam giác ABC, biết: A = 68 , AB = 5,0cm, AC = 5,7cm (làm tròn các độ dài đến chữ số thập phân thứ nhất, làm tròn các số đo góc đến độ).
Bài 1: Tính diện tích hình chữ nhật biết độ dài hai cạnh là 94,54m và 21,02 m ( làm tròn số đến kết quả đến chữ số thập phân thứ nhất).
Bài 2: Viết các phân số sau dưới dạng số hập phân gần đúng (làm tròn đến chữ số thập phân thứ hai)
Bài 1:
\(S_{hcn}=94,54\cdot21,02\approx1987,2\left(m^2\right)\)
Bài 1 :
Diện tích HCN là
94,54 . 21,02 =1987,2 m2
Bài 2: có phân số nào đâu
Bài 1:
94,54 x 21,02 = 1987, 2 m2
Bài 2:
\(\dfrac{6}{13}\) = 0.46153..... xấp xỉ 0.46
\(\dfrac{5}{3}\) = 1.6666..... xấp xỉ 1.67
\(\dfrac{5}{11}\) = 0.4545..... xấp xỉ 0.45
CHÚC BẠN HỌC TỐT!
Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
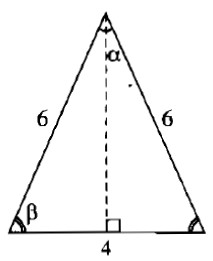
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.
cho tam giác ABC vuông tại A, B = 60° BC = 20 cm giải tam giác vuông ABC ( làm tròn đến độ đối với số đo góc làm tròn đến chữ số thập phân thứ tư đối với số đo độ dài )
\(AB=\cos B\cdot BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\\ AC=\sin B\cdot BC=\dfrac{\sqrt{3}}{2}\cdot20=10\sqrt{3}\approx17,3205\left(cm\right)\\ \widehat{C}=90^0-\widehat{B}=30^0\)
Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm. (làm tròn kết quả đến chữ số thập phân thứ nhất)
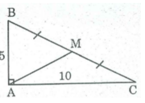
Giả sử tam giác ABC có ∠ A = 90 0 , M trung điểm BC; AB = 5cm, AC = 10cm
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2
BC = 5 2 + 10 2 = 125 ≈ 11,2 (cm)
Mà AM = 1/2 BC (tính chất tam giác vuông)
⇒ AM = 1/2 .11,2 = 5,6 (cm)
Một cái mái nhà được thiết kế theo hình tam giác ADE cân tại A có AH vuông góc với DE, AH= 1.2m, AD=AE=4m Độ dài DE bằng .......m? (làm tròn đến chữ số thập phân thứ nhất sau dấu phẩy)
Ta thấy: do tam giác ABC cân nên đường cao AH cũng là đường trung tuyến của tam giác ADE. Suy ra HD=HE.
Xét tam giác ADH vuông tại H. Áp dụng định lí Pytago ta có:
AH2+HD2=AD2
(1,2)2+HD2=42
1,44+HD2=16
HD2=16-1,44=14,56(m)
=>HD=\(\frac{2\sqrt{91}}{5}\)(m)
=>ED=\(\frac{4\sqrt{91}}{5}\)\(\approx\)7,6m
Tính diện tích hình thang cân, biết hai cạnh đáy là 12 cm và 18 cm, góc ở đáy bằng \(75^0\) ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
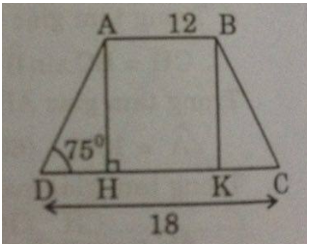
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, D^=75∘
Kẻ AH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).
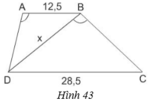
Tính độ dài x của đoạn thẳng BD trong hình 43 (làm tròn đến chữ số thập phân thứ nhất), biết rằng ABCD là hình thang (AB // CD); AB = 12,5cm, CD = 28,5cm, góc DAB = góc DBC.
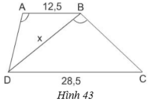
Tính độ dài x của đoạn thẳng BD trong hình 43 (làm tròn đến chữ số thập phân thứ nhất), biết rằng ABCD là hình thang (AB // CD); AB = 12,5cm, CD = 28,5cm, góc DAB = góc DBC.
Tính đường chéo d của một hình chữ nhật, biết độ dài các cạnh a = 3cm, b = 5cm (làm tròn kết quả đến chữ số thập phân thứ nhất)
Theo định lý Py-ta-go :
\(d^2=a^2+b^2=3^2+5^2=34\)
hay \(d=\sqrt{34}\approx5,8\left(cm\right)\)
Giả sử hình chữ nhật ABCD có AB = a = 3cm; BC = b = 5cm; BD = d
Trong tam giác vuông ABC theo định lý Py-ta-go ta có:
d2=a2+b2⇒d2=32+52=9+25=34d=√34≈5,8(cm)