cho 4 điểm A(0,5); B(1,-2); C(2,1); D(2,5;2,5) chứng minh 4 điểm A,B,C,D thẳng hàng

Những câu hỏi liên quan
cho 4 điểm A(0,5); B(1,-2); C(2,1); D(2,5;2,5) chứng minh 4 điểm A,B,C,D thẳng hàng
Bài 4: (0,5 điểm)
Cho tổng A = 20 + 21 + 22 + 23 + 24 + 25 + .... + 2100
Tính A
uhm...Mik dg thắk mắk là cái 0,5 điểm để lmj._.
Đúng 0
Bình luận (2)
\(A=\left[\left(2100-20\right):1+1\right]\cdot\left(2100+20\right):2\)
\(A=2081\cdot1060\)
Đúng 1
Bình luận (3)
Bài 2: (0,5 điểm). Cho đa thức 2 A x x 2 3 5 . Tính giá trị của A tại 𝑥 − 2.Bài 3: (2,0 điểm). Một hình chữ nhật có chiều dài hơn chiều rộng 10 m, biết chiều dài và chiều rộng tỉ lệ với 7; 5. Tính diện tích của hình chữ nhật đó.Bài 4.(0,5 điểm) Một cửa hàng bán tivi nhập về với giá 12 325 000 đồng 1 tivi. Hỏi cửa hàng đó phải bán với giá bao nhiêu tiền một tivi để được lãi 15% so với giá bán? Bài 5. (3 điểm) Cho tam giác ABC có AB AC. Gọi H là trung điểm của BC, trên tia đối của tia AH lấy điể...
Đọc tiếp
Bài 2: (0,5 điểm). Cho đa thức 2 A x x 2 3 5 . Tính giá trị của A tại 𝑥 = − 2.
Bài 3: (2,0 điểm). Một hình chữ nhật có chiều dài hơn chiều rộng 10 m, biết chiều dài và chiều rộng tỉ lệ với 7; 5. Tính diện tích của hình chữ nhật đó.
Bài 4.(0,5 điểm) Một cửa hàng bán tivi nhập về với giá 12 325 000 đồng 1 tivi. Hỏi cửa hàng đó phải bán với giá bao nhiêu tiền một tivi để được lãi 15% so với giá bán?
Bài 5. (3 điểm) Cho tam giác ABC có AB < AC. Gọi H là trung điểm của BC, trên tia đối của tia AH lấy điểm D sao cho AH = DH. a) Chứng minh ∆ ABH = ∆ DCH, từ đó suy ra AB // CD. b) Vẽ đường cao AM (M thuộc BC), trên tia đối của tia MA, lấy điểm N sao cho MA=MN . Chứng minh tam giác HAN cân tại H.

5:
a: Xét ΔABH và ΔDCH có
HA=HD
góc AHB=góc DHC
HB=HC
=>ΔABH=ΔDCH
=>góc ABH=góc DCH
=>AB//CD
b: Xét ΔHAN co
HM vừa là đường cao, vừa là trung tuyến
=>ΔHAN cân tại H
Đúng 0
Bình luận (0)
Cho \(A=1+3+3^2+3^3+3^4+...+3^{90}\). Chứng minh rằng \(A\) không phải là số chính phương
(0,5 điểm của mình đó)
Lời giải:
$A=1+3+3^2+(3^3+3^4+3^5+3^6)+.....+(3^{87}+3^{88}+3^{89}+3^{90}$
$=13+3^3(1+3+3^2+3^3)+....+3^{87}(1+3+3^2+3^3)$
$=13+(1+3+3^2+3^3)(3^3+....+3^{87})$
$=13+40(3^3+....+3^{87})=3+10+40(3^3+...+3^{87})$ chia $5$ dư $3$
$\Rightarrow A$ không là scp.
Đúng 1
Bình luận (0)
Câu 7. (0,5 điểm) Phép chia 154 : 12 được thương là 12,8 và số dư là:A. 40 B. 4 C. 0,4 D. 0,04Câu 8. (0,5 điểm) 12,5% số học sinh của khối 5 là 24 bạn. Để tìm số học sinh của khối 5, ta cần tính thế nào cho đúng?A)24 x 12,5 B. 24 : 12,5C. 24 x 12,5 : 100 D. 24 : 12,5 x 100CÍU TUI VỚI M.N ƠI HUHU
Đọc tiếp
Câu 7. (0,5 điểm) Phép chia 154 : 12 được thương là 12,8 và số dư là:
A. 40 B. 4 C. 0,4 D. 0,04
Câu 8. (0,5 điểm) 12,5% số học sinh của khối 5 là 24 bạn. Để tìm số học sinh của khối 5, ta cần tính thế nào cho đúng?
A)24 x 12,5 B. 24 : 12,5
C. 24 x 12,5 : 100 D. 24 : 12,5 x 100
CÍU TUI VỚI M.N ƠI HUHU
Câu 7: \(154=12.12,8+0,4\) khoanh C
Câu 8: 24 : 12,5% = 24 : (12,5 : 100) = 24: 12,5 x 100 = 192
Khoanh D
Đúng 0
Bình luận (0)
Câu 4 (0,5 điểm) Cho x + y = 20. Tìm GTLN của xy
Bài 4: (0,5 điểm) Cho ΔABC biết A420, C670. Tính Bài 5: (3 điểm) Cho ΔABC có ba góc nhọn (AB AC). Gọi M là trung điểm của BC. Vẽ tia AM, trên tia AM lấy điểm D sao cho MA MD.a/ Chứng minh ΔAMB ΔDMCb/ Chứng minh AB // CDc/ kẻ tia Ax // BC (Ax và BC cùng thuộc nữa mặt phẳng bờ là AB) .Trên tia Ax lấy điểm N sao cho AN BC . Chứng minh D,C,N thẳng hàng.
Đọc tiếp
Bài 4: (0,5 điểm) Cho ΔABC biết A=420, C=670. Tính
Bài 5: (3 điểm) Cho ΔABC có ba góc nhọn (AB < AC). Gọi M là trung điểm của BC. Vẽ tia AM, trên tia AM lấy điểm D sao cho MA = MD.
a/ Chứng minh ΔAMB = ΔDMC
b/ Chứng minh AB // CD
c/ kẻ tia Ax // BC (Ax và BC cùng thuộc nữa mặt phẳng bờ là AB) .Trên tia Ax lấy điểm N sao cho AN = BC . Chứng minh D,C,N thẳng hàng.
Bài 4: ( 2,0 điểm) Cho cân tại A. Kẻ AH vuông góc BC tại H.a) ( 0,75 điểm) Chứng minh : ABH ACHb) ( 0,75 điểm) Từ H kẻ HI // AB ( I thuộc AC). Chứng minh: tam giác AIH cân.c) ( 0,5 điểm ) Chứng minh :I là trung điểm của AC.
Đọc tiếp
Bài 4: ( 2,0 điểm) Cho ![]() cân tại A. Kẻ AH vuông góc BC tại H.
cân tại A. Kẻ AH vuông góc BC tại H.
a) ( 0,75 điểm) Chứng minh : ![]() ABH =
ABH = ![]() ACH
ACH
b) ( 0,75 điểm) Từ H kẻ HI // AB ( I thuộc AC). Chứng minh: tam giác AIH cân.
c) ( 0,5 điểm ) Chứng minh :I là trung điểm của AC.
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔABH=ΔACH
b: HI//AB
=>góc IHA=góc BAH
=>góc IHA=góc IAH
=>ΔIAH cân tại I
c: Xét ΔBAC có
H là trung điểm của CB
HI//AB
=>I là trung điểm của AC
Đúng 0
Bình luận (0)
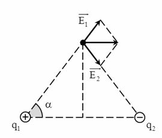
Hai điện tích điểm q 1 = 0,5 nC và q 2 = - 0 , 5 nC đặt tại hai điểm A và B cách nhau 6 cm trong không khí. Tính cường độ điện trường tại điểm M nằm trên trung trực của AB, cách trung điểm I của AB một đoạn 4 cm.