Quan sát Hình 26.
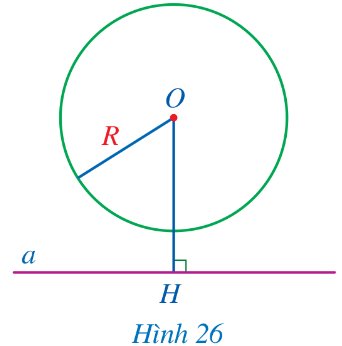
a) Cho biết đường thẳng a và đường tròn (O; R) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng OH và R.
Những câu hỏi liên quan
Quan sát Hình 84 và cho biết:
a) Khoảng cách từ điểm O đến đường thẳng a;
b) Khoảng cách từ điểm O đến đường thẳng b;
c) Khoảng cách từ điểm O đến đường thẳng c.
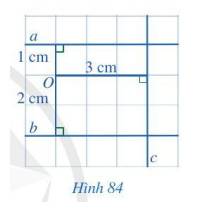
a) Khoảng cách từ điểm O đến đường thẳng a bằng 1 cm;
b) Khoảng cách từ điểm O đến đường thẳng b bằng 2 cm;
c) Khoảng cách từ điểm O đến đường thẳng c bằng 3 cm.
Đúng 0
Bình luận (0)
Cho hình trụ có hai đường tròn đáy là (O) và (O). Gọi A trên đường tròn ( O) và B trên đường tròn (O) sao cho AB 4a. Biết khoảng cách từ đường thẳng AB đến trục của hình trụ a là OO2a. Tính diện tích xung quanh của hình trụ đã cho A. 42πa2 B. 8a2 C. 16πa2 D. 8πa2
Đọc tiếp
Cho hình trụ có hai đường tròn đáy là (O) và (O'). Gọi A trên đường tròn ( O) và B trên đường tròn (O') sao cho AB = 4a. Biết khoảng cách từ đường thẳng AB đến trục của hình trụ a là OO'=2a. Tính diện tích xung quanh của hình trụ đã cho
A. 42πa2
B. 8a2
C. 16πa2
D. 8πa2
Giải mục 1 trang 95, 96, 97 SGK Toán 11 tập 1 - Cánh Diều
14 tháng 7 2023 lúc 16:00
a) Hãy nêu các vị trí tương đối của hai đường thẳng trong mặt phẳng.
b) Quan sát hai đường thẳng a và b trong Hình 31a, 31b và cho biết các đường thẳng đó có cùng nằm trong một mặt phẳng không
a) Các vị trí tương đối của hai đường thẳng trong mặt phẳng:
- Hai đường thẳng không có điểm chung thì hai đường thẳng song song
- Hai đường thẳng có một điểm chung thì hai đường thẳng cắt nhau
- Hai đường thẳng có rất nhiều điểm chung thì hai đường thẳng trùng nhau
b) Hai đường thẳng a và b ở Hình 31a cùng nằm trong một mặt phẳng
Hai đường thẳng a và b ở Hình 31b không cùng nằm trong một mặt phẳng.
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính 10cm và đường thẳng d. Gọi H là hình chiếu vuông góc của O trên đường thẳng d. Biết OH 8cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O). A. Đường thẳng d và đường tròn (O) tiếp xúc nhau. B. Đường thẳng d và đường tròn (O) cắt nhau. C. Đường thẳng d và đường tròn (O) có điểm chung. D. Đường thẳng d và đường tròn(O) không có điểm chung.
Đọc tiếp
Cho đường tròn (O) đường kính 10cm và đường thẳng d. Gọi H là hình chiếu vuông góc của O trên đường thẳng d. Biết OH = 8cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O).
A. Đường thẳng d và đường tròn (O) tiếp xúc nhau.
B. Đường thẳng d và đường tròn (O) cắt nhau.
C. Đường thẳng d và đường tròn (O) có điểm chung.
D. Đường thẳng d và đường tròn(O) không có điểm chung.
a) Kẻ OH ⊥⊥ d
=> OH là khoảng cách từ d tới tâm đường tròn (O)
mà OH < R (3 < 5)
=> Đường thẳng d cắt đường tròn (O)
b) Xét ΔΔOAH vuông tại H có:
OH2+AH2=OA2OH2+AH2=OA2 (ĐL Pi-ta-go)
=> AH=OA2−OH2−−−−−−−−−−√=52−32−−−−−−√=4(cm)AH=OA2−OH2=52−32=4(cm)
Xét (O): AB là dây, OH ⊥⊥ AB
=> H trung điểm AB (quan hệ ⊥⊥ giữa đường kính và dây cung)
=> AB = 2AH = 8(cm)
c) Xét ΔΔABC có: O, H trung điểm AC, AB
=> OH là đường trung bình ΔΔABC
=> OH // BC mà OH ⊥⊥ AH
=> BC ⊥⊥ AH => ΔΔABC vuông tại B
=> AB2 + BC2 = AC2
=> BC=102−82−−−−−−−√=6(cm)BC=102−82=6(cm)
Xét ΔΔABC vuông tại B
có: sinC=ABAC=810=45⇒Cˆ=53o7′sinC=ABAC=810=45⇒C^=53o7′
=> Aˆ=36o52′A^=36o52′
d) Xét ΔΔACM vuông tại C: CB ⊥⊥ AM
có: AC2=AB⋅AMAC2=AB⋅AM (HTL tam giác vuông)
=> AM=AC2AB=1028=12,5(cm)AM=AC2AB=1028=12,5(cm)
lại có: AB + BM = AM ; AB = 8(cm)
=> BM = 4,5(cm)
Cho hình trụ T có trục OO Trên hai đường tròn đáy (O) và (O) lần lượt lấy hai điểm A và B sao cho AB a và đường thẳng AB tạo với đáy của hình trụ góc
60
∘
. Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B. Biết rằng
A
O
B
^
120
∘
. Tính khoảng cách d giữa hai đường thẳng AB và O
Đọc tiếp
Cho hình trụ T có trục OO' Trên hai đường tròn đáy (O) và (O') lần lượt lấy hai điểm A và B sao cho AB = a và đường thẳng AB tạo với đáy của hình trụ góc 60 ∘ . Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B'. Biết rằng A O B ^ = 120 ∘ . Tính khoảng cách d giữa hai đường thẳng AB và O
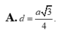
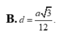
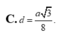
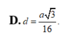
Cho đường tròn (O) và đường thẳng a. Kẻ OH ⊥ a tại H, biết OH > R khi đó đường thẳng a và đường tròn (O)
A. cắt nhau
B. không cắt nhau
C. tiếp xúc
D. đáp án khác
Cho đường tròn (O) và đường thẳng a. Kẻ OH ⊥ a tại H, biết OH > R khi đó đường thẳng a và đường tròn (O)
A. cắt nhau
B. không cắt nhau
C. tiếp xúc
D. đáp án khác
Chọn đáp án B
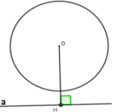
Vì OH > R nên α không cắt (O)
Đúng 0
Bình luận (0)
vẽ đường tròn tâm O bán kính 2 cm.Lấy các điểm A,B,C,D sao cho OA=2 cm;OB=1,5 cm;OC=3 cm; OD=2 cm và 3 điểm A,B,D thẳng hàng.Hãy cho biết quan hệ của các điểm A,B,C,D đối với đường tròn tâm O và tên của đoạn thẳng OA,OB,AD đối với đường tròn tâm O.
Cho hình trụ T có trục OO Trên hai đường tròn đáy (O) và (O) lần lượt lấy hai điểm A và B sao cho AB a và đường thẳng AB tạo với đáy của hình trụ góc
60
°
Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B Biết rằng
A
O
B
^
120
°
Tính khoảng cách d giữa hai đường thẳng AB và OO A.
d
a...
Đọc tiếp
Cho hình trụ T có trục OO' Trên hai đường tròn đáy (O) và (O') lần lượt lấy hai điểm A và B sao cho AB = a và đường thẳng AB tạo với đáy của hình trụ góc 60 ° Gọi hình chiếu của B trên mặt phẳng đáy chứa đường tròn (O) là B' Biết rằng A O B ^ = 120 ° Tính khoảng cách d giữa hai đường thẳng AB và OO'
A. d = a 3 4
B. d = a 3 12
C. d = a 3 8
D. d = a 3 16
Quan sát hình 21 và cho biết những nhận xét sau đúng hay sai:
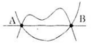
Hình 21
Chỉ có một đường thẳng đi qua hai điểm A và B.