Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C\left(x\right)=\dfrac{50x+2000}{x}\).
Tìm các đường tiệm cận của đồ thị hàm số y = C(x).
Những câu hỏi liên quan
Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x.
a) Tính chi phí trung bình \(\overline C \left( x \right)\) để sản xuất một sản phẩm.
b) Tính \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right)\) và cho biết ý nghĩa của kết quả.
a) \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{50000 + 105x}}{x}\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50000 + 105x}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{{50000}}{x} + 105} \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{50000}}{x} + 105} \right) = 0 + 105 = 105\)
Vậy khi số sản phẩm càng lớn thì chi phí trung bình để sản xuất một sản phẩm tối đa 105 (nghìn đồng).
Đúng 0
Bình luận (0)
Một nhà máy sản xuất được 60000 sản phẩm trong một ngày và tổng chi phí sản xuất x sản phẩm được cho bởi:
P
(
x
)
250000
+
0
,
08
x
+
200000000
x
Hỏi nhà máy nên sản xuất bao nhiêu sản phẩm mỗi ngày để chi phí sản xuất là nhỏ nhất? A. 30000 B. 40000 C. 50000 D. 60000
Đọc tiếp
Một nhà máy sản xuất được 60000 sản phẩm trong một ngày và tổng chi phí sản xuất x sản phẩm được cho bởi:
P ( x ) = 250000 + 0 , 08 x + 200000000 x
Hỏi nhà máy nên sản xuất bao nhiêu sản phẩm mỗi ngày để chi phí sản xuất là nhỏ nhất?
A. 30000
B. 40000
C. 50000
D. 60000
Ta có x ∈ (0; 60000)
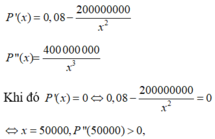
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C
Đúng 0
Bình luận (0)
Tổng chi phí T (đơn vị tính: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức \(T = {Q^2} + 30Q + 3300\); giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo không bị lỗ (giả thiết các sản phẩm được bán hết)?
Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.
Lợi nhuận khi bán Q sản phẩm là \(170Q - \left( {{Q^2} + 30Q + 3300} \right)\)\( = - {Q^2} + 140Q - 3300\)(nghìn đồng)
Để không bị lỗ thì \( - {Q^2} + 140Q - 3300 \ge 0\left( 1 \right)\)
\(a = - 1 < 0;\Delta ' = 1600\)
\( - {Q^2} + 140Q - 3300 = 0\) có 2 nghiệm phân biệt \({x_1} = 30,{x_2} = 110\)
(1)\( \Leftrightarrow \)\(30 \le x \le 110\)
Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.
Đúng 0
Bình luận (0)
SGK Toán 8 tập 1– Chân trời sáng tạo
22 tháng 7 2023 lúc 9:00
Giá thành trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức \(C(x) = \dfrac{{0,0002{x^2} + 120x + 1000}}{x}\), trong đó \(x\) là số áo được sản xuất và \(C\) tính bằng nghìn đồng. Tính \(C\) khi \(x = 100\), \(x = 1000\)
Khi x=100 thì \(C=\dfrac{0.0002\cdot100^2+120\cdot100+1000}{100}=\dfrac{6501}{50}\)
Khi x=1000 thì \(C=\dfrac{0.0002\cdot1000^2+120\cdot1000+1000}{1000}=\dfrac{606}{5}\)
Đúng 1
Bình luận (0)
SGK Cánh Diều
25 tháng 7 2023 lúc 15:34
Một xưởng sản xuất thủ công mỹ nghệ sản xuất được 315 sản phẩm làm bằng cây lục bình trong 9 ngày. Hỏi:
a) Trung bình mỗi ngày xưởng thủ công đó sản xuất được bao nhiêu sản phẩm làm bằng cây lục bình?
b) Với sản lượng như trên, để sản xuất được 280 sản phẩm xưởng thủ công đó cần sản xuất trong mấy ngày?
a) Trung bình mỗi ngày xưởng thủ công đó sản xuất được số sản phẩm làm bằng cây lục bình là:
315 : 9 = 35 (sản phẩm)
b) Với sản lượng như trên, để sản xuất được 280 sản phẩm xưởng thủ công đó cần sản xuất trong số ngày là:
280 : 35 = 8 (ngày)
Đúng 1
Bình luận (1)
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phảm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm v...
Đọc tiếp
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phảm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là:
A. 32 triệu đồng
B. 35 triệu đồng
C. 14 triệu đồng
D. 30 triệu đồng
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đòng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, BÌnh phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình khôn...
Đọc tiếp
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đòng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, BÌnh phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
A. 32 triệu đồng
B. 35 triệu đồng
C. 14 triệu đồng
D. 30 triệu đồng
Công ty A có ba phân xưởng là X, Y và Z. Phân xưởng X sản xuất được 25000 sản phẩm trong
một ngày. Phân xưởng Y sản xuất được ít hơn phân xưởng X 500 sản phẩm trong một ngày.
Phân xưởng Y sản xuất được nhiều hơn phân xưởng Z 600 sản phẩm một ngày. Hỏi công ty A sản
xuất được bao nhiêu sản phẩm trong một ngày?
Phân xưởng Y sản xuát được:
25000-500=24500(sp)
Phân xưởng Z sản xuất được:
24500-600=23900(sp)
Công ty A sản xuất đc:
24500+23900+25000=73400(sp)
Đúng 1
Bình luận (0)
Một công ty sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) với x < 60 thì có doanh thu là \( - 5{x^2} + 50x + 15000\)(nghìn đồng). Tính số sản phẩm mà công ty đã bán được theo x.
Giá của sản phẩm sau khi tăng giá là: \(x + 50\)(nghìn đồng).
Số sản phẩm mà công ty bán được sau khi tăng giá là:
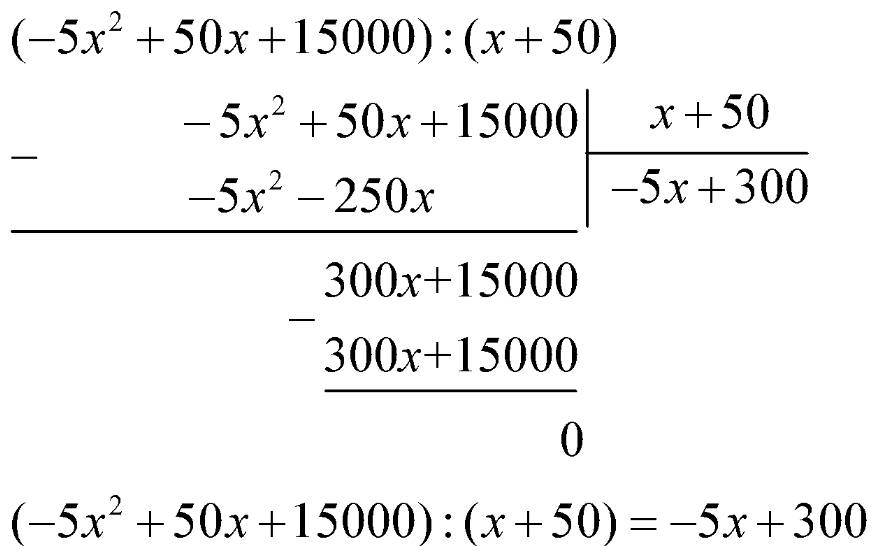
Vậy số sản phẩm mà công ty đã bán được theo x là \( - 5x + 300\) (sản phẩm).
Đúng 0
Bình luận (0)
Một phân xưởng được giao sản xuất một lô hàng. Ban quản lí phân xưởng tính rằng nếu 10 công dân, mỗi người sản xuất 60 sản phẩm một ngày thì sẽ hoàn thành trong 20 ngày. Hỏi nếu 20 công dân, mỗi người làm 75 sản phẩm thì hoàn thành trong bao nhiêu ngày?
Xem chi tiết
Giúp mik với mik đang cần gấp
Gíup mik với mn ui.Tối mik phải đii học rùi ai đúng mik tick cho.
Đúng 0
Bình luận (0)
Như vậy trong 1 ngày số sản phẩm của 10 công nhân làm được là: 10x60=600 sản phẩm
Số sản phẩm cần phải làm theo kế hoạch: 600x20=12000 sản phẩm
20 công nhân, mỗi công nhân san xuất 75 sản phẩm thì trong 1 ngày sản xuất được: 75x20=1500 sản phẩm.
Số ngày để làm xong kế hoạch: 12000:1500=8 ngày
#Cố lên
Đúng 2
Bình luận (0)
Phân xưởng phải sản xuất số sản phẩm là:
10 x 60 x 20 = 12000 sản phẩm
Số ngày mỗi người làm được 75 sản phẩm là:
12000 : 20 : 75 = 8 ngày
Đúng 2
Bình luận (0)
Xem thêm câu trả lời