Trên Google Maps, thực hiện phép đo khoảng cách từ vị trí 0°N, 0°E đến vị trí 45°N, 30°E và so sánh với kết quả tính được ở Luyện tập 5.

Những câu hỏi liên quan
Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A 45 ° 30 ° C A B Câu 4. Cho đường tròn (O) đường kính AB 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA CB. Tiếp tuyến tại A của đường tròn (O) cắt BC tại Ea) Chứng minh tam giác ABC vuông và BC.BE4R2b) Đường thẳng qua A vuông góc với OE tạ...
Đọc tiếp
Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A
Câu 4. Cho đường tròn (O) đường kính AB = 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA < CB. Tiếp tuyến tại A của đường tròn (O) cắt BC tại E
a) Chứng minh tam giác ABC vuông và BC.BE=4R2
b) Đường thẳng qua A vuông góc với OE tại I và cắt đường tròn (O) tại D. Chứng minh bồn điểm A, E,C,I cùng thuộc một đường tròn.
c) Chứng minh ED là tiếp tuyến của đường tròn (O) và góc ECD = góc EDB
Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)
Đúng 0
Bình luận (0)
Hai bạn An ( vị trí A) và Bình ( vị trí B) đang đứng ở mặt đất bằng phẳng cách nhau 150m thì nhìn thấy một máy bay điều khiển từ xa ( vị trí T). Biết khoảng cách từ An đến máy bay là 80m và khoảng cách từ Bình đến máy bay là 117m. Tính góc nâng để nhìn thấy máy bay tại vị trí của An ( góc TAB) và góc nâng để nhìn thấy may bay từ vị trí của Bình ( góc TBA ). ( kết quả làm tròn đến hàng đơn vị và số đo góc làm tròn đến độ)
Đọc tiếp
Hai bạn An ( vị trí A) và Bình ( vị trí B) đang đứng ở mặt đất bằng phẳng cách nhau 150m thì nhìn thấy một máy bay điều khiển từ xa ( vị trí T). Biết khoảng cách từ An đến máy bay là 80m và khoảng cách từ Bình đến máy bay là 117m. Tính góc nâng để nhìn thấy máy bay tại vị trí của An ( góc TAB) và góc nâng để nhìn thấy may bay từ vị trí của Bình ( góc TBA ). ( kết quả làm tròn đến hàng đơn vị và số đo góc làm tròn đến độ)
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Nguyễn Văn Phú
Thực hiện thí nghiệm giao thoa I-âng bằng ánh sáng đơn sắc có bước sóng
λ
0
,
5
μ
m
. Khoảng cách giữa hai khe bằng 0,5 mm và khoảng cách từ hai khe đến màn quan sát E bằng 200 cm. Tại vị trí M trên màn E có toạ độ 7mm là vị trí A. vân sáng bậc 7. B. vân tối thứ 7. C. vân tối thứ 4. D. vân sáng bậc 4.
Đọc tiếp
Thực hiện thí nghiệm giao thoa I-âng bằng ánh sáng đơn sắc có bước sóng λ = 0 , 5 μ m . Khoảng cách giữa hai khe bằng 0,5 mm và khoảng cách từ hai khe đến màn quan sát E bằng 200 cm. Tại vị trí M trên màn E có toạ độ 7mm là vị trí
A. vân sáng bậc 7.
B. vân tối thứ 7.
C. vân tối thứ 4.
D. vân sáng bậc 4.
Thực hiện thí nghiệm giao thoa I-âng bằng ánh sáng đơn sắc có bước sóng
λ
0,5
μ
m. Khoảng cách giữa hai khe bằng 0,5 mm và khoảng cách từ hai khe đến màn quan sát E bằng 200 cm. Tại vị trí M trên màn E có toạ độ 7mm là vị trí A. Vân sáng bậc 7 B. Vân tối thứ 7 C. Vân tối thứ 4 D. Vân sáng bậc 4
Đọc tiếp
Thực hiện thí nghiệm giao thoa I-âng bằng ánh sáng đơn sắc có bước sóng λ = 0,5 μ m. Khoảng cách giữa hai khe bằng 0,5 mm và khoảng cách từ hai khe đến màn quan sát E bằng 200 cm. Tại vị trí M trên màn E có toạ độ 7mm là vị trí
A. Vân sáng bậc 7
B. Vân tối thứ 7
C. Vân tối thứ 4
D. Vân sáng bậc 4
Tính khoảng cách giữa hai điểm B và C, biết rằng từ vị trí A ta đo được: AB 234m, AC 185m và
B
A
C
^
53
0
(kết quả tính bằng mét và làm tròn đến hàng đơn vị). A. 190m B. 191m C. 192m D. 193m
Đọc tiếp
Tính khoảng cách giữa hai điểm B và C, biết rằng từ vị trí A ta đo được: AB = 234m, AC = 185m và B A C ^ = 53 0 (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
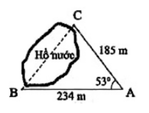
A. 190m
B. 191m
C. 192m
D. 193m
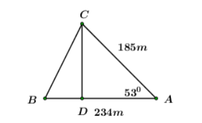
Từ C, dựng đường vuông góc với AB, cắt AB tại D.
Khi đó ta có: CD là đường cao của ABC.
Áp dụng tỉ số lượng giác của góc nhọn trong ACD vuông tại D ta có:
![]()
![]()
=> BD = AB – AD = 234 − 185. c o s 53 0
Áp dụng định lý Py-ta-go cho BCD để tính BC.
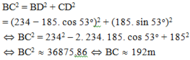
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
một chiếc tàu thủy đang neo đậu ở vị trí C trên biển và 2 người ở các vị trí A và B cách nhau 500m . Họ đo được góc CAB bằng 870 và góc CBA bằng 620 . Tính các khoảng cách AC và BC
người ta dự định bắc một cái cầu qua một con sông. Để đo khoảng cách giữa hai đầu A và B của cầu kĩ sư làm như sau. Một người đứng ở vị trí A, một người đứng ở vị trí C dọc trên cùng một bờ và tiến hành đo đạc. Kết quả đo được là khoảng cách AC=25m, góc BAC= 59 độ, góc BCA= 82 độ. Em hãy giúp kĩ sư tính khoảng cách giữa hai đầu cầu nhé
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)
Đúng 0
Bình luận (0)
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC 25 m, widehat {BAC} 59,{95^o};;widehat {BCA} 82,{15^o}. Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Đọc tiếp
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\) Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
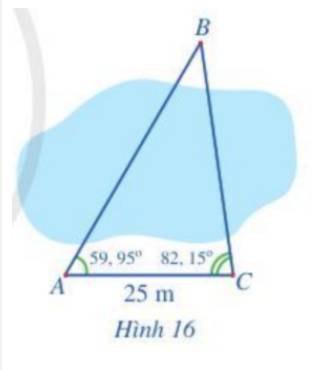
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.
Đúng 0
Bình luận (0)
Từ trên đỉnh của 1 ngọn đền , ngừoi ta nhìn thấy hai vị trí E và F với 2 góc hạ lần lượt là 45,5 độ và 26 độ . biết ngọn đền cao 38m . Tính khoảng cách giữa Evà F (làm tròn kết quả đến 0,01) -trình bày lời giải đấy đủ ^^
a) Mai có các thẻ từ số 0 đến 9. Mai có thể đặt thẻ số nào vào vị trí dấu “?” để được phép so sánh đúng?

b) Mai có tất cả bao nhiêu cách chọn thẻ số phù hợp với yêu cầu trên?
a) Mai có thể đặt số 8 hoặc số 9.
b) Mai có tất cả 2 cách chọn thẻ là chọn thẻ ghi số 8 hoặc thẻ ghi số 9.
Đúng 0
Bình luận (0)