hãy đổi chỗ 2 tấm thẻ để nhận được một số lẻ lớn nhất.
863749
helpppppppppppppppppp![]()
Xếp 9 tấm thẻ để được số 118 252 018. Em hãy
a. Lấy ra một tấm thẻ để được một số lẻ.
b. Lấy ra một tấm thẻ để được một số mà khi làm tròn đến hàng trăm nghìn thì được 11 900 000.
Trên bản có các tấm thẻ ghép được thành số 1 951 890

a) Lấy ra một tấm thẻ để được số có sáu chữ số lớn nhất có thể
b) Lấy ra một tấm thẻ để được số có sáu chữ số bé nhất có thể
a) Lấy ra tấm thẻ số 0. Ta được số có sáu chữ số lớn nhất có thể là: 998 511
b) Lấy ra tấm thẻ số 9. Ta được số có sáu chữ số bé nhất có thể là: 101 589
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
A. 75 94
B. 25 646
C. 170 646
D. 175 646

Trong 20 tấm thẻ từ 1 đến 20 có 10 tấm thẻ mang số lẻ, 10 tấm thẻ mang số chẵn trong đó có 5 tấm thẻ chia hết cho 5. Gọi A là biến cố: " chọn có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4"
TH1: Chọn được 3 tấm thẻ mang số lẻ 1 tấm thẻ mang số chẵn chia hết cho 4 và một tấm chẵn mang số không chia hết cho 4 có: ![]()
TH2: Chọn được 3 tấm thẻ mang số lẻ và 2 tấm thẻ mang số chẵn và chia hết cho 4 có:

Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 8 tấm , tính xác suất để chọn được 5 tấm mang số lẻ, 3 tấm mang số chẵn trong đó ít nhất 2 tấm thẻ mang số chia hết cho 3.
Trong các số từ 1 tới 20, có 3 số lẻ chia hết cho 3 là \(\left\{3;9;15\right\}\), 3 số chẵn chia hết cho 3 là \(\left\{6;12;18\right\}\), có 7 số lẻ ko chia hết cho 3, 7 số chẵn ko chia hết cho 3
Chọn 8 thẻ bất kì: \(C_{20}^8\) cách
Chọn 8 thẻ trong đó ko thẻ nào chia hết cho 3: có \(C_7^5.C_7^3\) cách
Chọn 8 thẻ trong đó có đúng 1 thẻ chia hết cho 3:
TH1: thẻ chia hết cho 3 là thẻ chẵn: \(C_3^1.C_7^2.C_7^5\) cách
TH2: thẻ chia hết cho 3 là thẻ lẻ: \(C_3^1.C_7^4.C_7^3\) cách
Xác suất: \(\dfrac{C_{20}^8-\left(C_7^3.C_7^5+C_3^1.C_7^2.C_7^5+C_3^1.C_7^4.C_7^3\right)}{C_{20}^8}=...\)
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 8 tấm , tính xác suất để chọn được 5 tấm mang số lẻ, 3 tấm mang số chẵn trong đó ít nhất 2 tấm thẻ mang số chia hết cho 4. Kết quả đúng là:
A. 1008 4199
B. 3695 4199
C. 504 4199
D. 3191 4199
Đáp án C
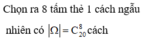
Trong 20 tấm thẻ có 10 tấm mang
số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn
chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có
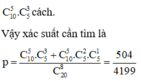
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 8 tấm , tính xác suất để chọn được 5 tấm mang số lẻ, 3 tấm mang số chẵn trong đó ít nhất 2 tấm thẻ mang số chia hết cho 4. Kết quả đúng là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án C
Chọn ra 8 tấm thẻ 1 cách ngẫu nhiên có ![]() cách
cách
Trong 20 tấm thẻ có 10 tấm mang số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có: ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có ![]() cách.
cách.
Vậy xác suất cần tìm là
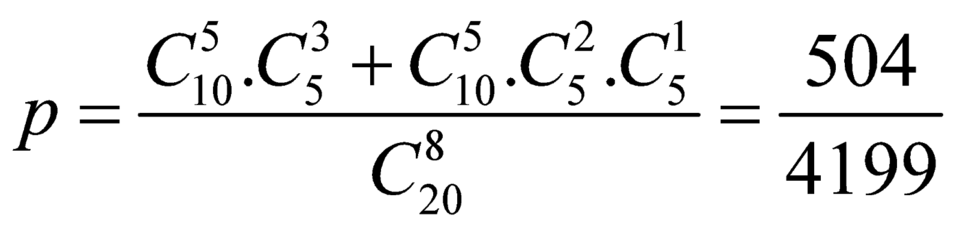
Đố em
Số 178 265 được ghép từ 6 thẻ số như hình dưới đây.

Mỗi lượt di chuyển, Nam chỉ có thể đổi chỗ hai tấm thẻ cho nhau. Hỏi Nam cần ít nhất mấy lượt di chuyển để được số 268 157?
Nam cần ít nhất 3 lượt di chuyển để được số 268 157
+ Lượt 1: di chuyển tấm thẻ số 2 và tấm thẻ số 6 lên đầu. Lúc này ta được số 261 785
+ Lượt 2: di chuyển tấm thẻ số 8 lên sau số 6. Ta được số 268 175
+ Lượt 3: di chuyển tấm thẻ số 5 lên sau số 1. Ta được số 268 157
Có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên 5 tấm thẻ. Xác suất trong 5 tấm được chọn có 3 tấm mang số lẻ, 3 tấm thẻ mang số chẵn trong đó có ít nhất một tấm thẻ mang số chia hết cho 4 là
A. 75/94.
B. 125/646.
C. 170/646.
D. 175/646
Có 10 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và có đúng một tấm thẻ mang số chia hết cho 10.
![]()
![]()
![]()

Có 10 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để trong 10 tấm thẻ có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn và có đúng một tấm thẻ mang số chia hết cho 10.
A. 99 667
B. 634 667
C. 33 667
D. 568 667