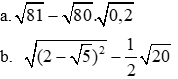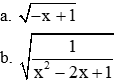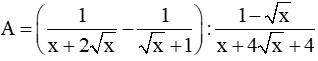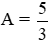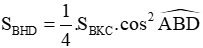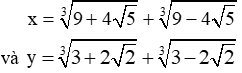giải bài tập toán : thu gọn biểu thức :A=(x-1)^2+(x+1)^2-(x-1)(x+1)

Những câu hỏi liên quan
giải bài tập toán : thu gọn biểu thức :B=(x-1)(x^2-x+1).(2x+2)(3x^2++3x+3)
=> B= (x-1)(x^2-x+1).2(x+1)3(x^2+x+1)
=> B= 6(x-1)(x^2+x+1).(x+1)(x^2-x+1)
=>B =6(x^3-1)(x^3+1)
=> B 6x^6-6
Đúng 0
Bình luận (0)
A. Bài 4: a, Thu gọn biểu thức -1/x2yz +5x2yz - x2yz và tính giá trị biểu thức tại x = -1, y = 2 và z = -1
B. b, Thu gọn biểu thức –x 2 z + 3x2 z – 7x2 z và tính giá trị biểu thức tại x = -1, z = -2
c, Thu gọn biểu thức 5xy2 + 0,5xy2 – 3xy2 và tính giá trị biểu thức tại x = 2, y =1 d, Thu gọn biểu thức -2y2 z 2 + 8y2 z 2 – y 2 z 2 và tính giá trị biểu thức tại y = -2, z = 0
Bài 4:
b: \(=x^2z\left(-1+3-7\right)=-5x^2z=-5\cdot\left(-1\right)^2\cdot\left(-2\right)=10\)
c: \(=xy^2\left(5+0.5-3\right)=2.5xy^2=2.5\cdot2\cdot1^2=5\)
Đúng 1
Bình luận (0)
Giải giúp mình bài toán này với
Rút gọn biểu thức sau: C= 4*(x-1)*(x+1)-5*x*(x-2)+x^2
So sánh với đáp số cho sẵn : 10*x-4
Bài 1. Thu gọn các biểu thức sau:
a) (x + 3)^3 + (x^2 + 1)(x – 2)
b) (2x – 1)^2 – (2 – x)^3
a.ta có
\(\left(x+3\right)^3+\left(x^2+1\right)\left(x-2\right)=x^3+9x^2+27x+27+x^3-2x^2+x-2\)
\(=2x^3+7x^2+28x+25\)
b.\(\left(2x-1\right)^2-\left(2-x\right)^3=4x^2-4x+1+x^3-6x^2+12x-8\)
\(=x^3-2x^2+8x-7\)
a) (x + 3)3 + (x2 + 1)(x - 2)
= x3 + 9x2 + 27x + 27 + x3 - 2x + x - 2
= x3 + x3 + 9x2 + 27x - 2x + x + 27 - 2
= 2x3 + 9x2 + 26x + 25
b) (2x - 1)2 - (2 - x)3
= 4x2 - 4x + 1 - ( 8 - 12x + 6x2 - x3)
= 4x2 - 4x + 1 - 8 + 12x - 6x2 + x3
= x3 + 4x2 - 6x2 + 12x - 4x + 1 - 8
= x3 - 2x2 + 8x - 7
Bài 60 (trang 33 SGK Toán 9 Tập 1)
Cho biểu thức $B=\sqrt{16 x+16}-\sqrt{9 x+9}+\sqrt{4 x+4}+\sqrt{x+1}$ với $x \geq-1$.
a) Rút gọn biểu thức $B$;
b) Tìm $x$ sao cho $B$ có giá trị là $16$.
\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)
a) B = 4√x+1 b) x = 15
Xem thêm câu trả lời
Bài 1:
A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
a) Tìm tập xác định của biểu thức A
b) Rút gọn biểu thức A
c) Chứng minh rằng A>0 với mọi x≠1
d) Tìm x để A đạt GTLN, tìm GTLN đó
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
Đúng 0
Bình luận (0)
c: Ta có: \(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
\(\Leftrightarrow\dfrac{2}{x+\sqrt{x}+1}>0\forall x\)
Đúng 0
Bình luận (0)
Bài 3. Thu gọn các biểu thức sau:
a) x(x + 1) – 2x(x – 2)
b) -3x( x – 1) + (x – 1)(x + 1)
c) (3x – 2)(3x + 2) – (x – 1)(x + 2)
a) x(x + 1) - 2x(x - 2) = x2 + x - 2x2 + 4x = -x2 + 5x
b) -3x(x - 1) + (x - 1)(x + 1) = -3x2 + 3x + x2 - 1 = -2x2 + 3x - 1
c) (3x - 2)(3x + 2) - (x - 1)(x + 2) = 9x2 - 4 - x2 - x + 2
= 8x2 - x - 2
a, x(x+1) - 2x(x -2 )
= x2 +x - 2x2 + 4x = -x2 + 5x
b, -3x( x - 1 ) + ( x -1 ) ( x+1 )
= -3x2 + 3x + x2 -1
= -2x2 + 3x -1
c, ( 3x-2 ) ( 3x + 2 ) - ( x -1 ) ( x +2 )
= 9x2 - 4 - ( x2 + 2x -x -2 )
= 9x2 -4 - x2 -2x + x + 2
= 8x2 -x -2
*Sxl
Trả lời:
a) x ( x + 1 ) - 2x ( x - 2 ) = x2 + x - 2x2 + 4x = - x2 + 5x
b) - 3x ( x - 1 ) + ( x - 1 ) ( x + 1 ) = - 3x2 + 3x + x2 - 1 = - 2x2 + 3x - 1
c) ( 3x - 2 ) ( 3x + 2 ) - ( x - 1 ) ( x + 2 ) = 9x2 - 4 - ( x2 + 2x - x - 2 ) = 9x2 - 4 - x2 - 2x + x + 2 = 8x2 - x - 2
Bài 1 (2,0 điểm).1. Thực hiện phép tính. 2. Tìm điều kiện của x để các biểu thức sau có nghĩa: Bài 2 (2,0 điểm).1. Phân tích đa thức thành nhân tử. 2. Giải phương trình: Bài 3 (2,0 điểm. Cho biểu thức: (với x 0; x ≠ 1)a. Rút gọn biểu thức A.b. Tìm x để Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC 8cm, BH 2cm.a. Tính độ dài các đoạn thẳng AB, AC, AH.b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK BH.BC.c. C...
Đọc tiếp
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
2. Giải phương trình:
Bài 3 (2,0 điểm. Cho biểu thức:
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 - 3(x + y) + 1993. Tính giá trị biểu thức P với:
Giúp vs ạ 1h nộp cô r
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
Đúng 1
Bình luận (0)
x3=18+33√(9+4√5)(9−4√5)(3√9+4√5+3√9−4√5)⇔x3=18+3x3√1⇔x3−3x=18y3=6+33√(3−2√2)(3+2√2)(3√3+2√2+3√3−2√2)⇔y3=6+3y3√1⇔y3−3y=6P=x3+y3−3(x+y)+1993P=(x3−3x)+(y3−3y)+1993P=18+6+1993=2017
Đúng 1
Bình luận (0)
Bài 1 (2,0 điểm).1. Thực hiện phép tính.2. Tìm điều kiện của x để các biểu thức sau có nghĩa:Bài 2 (2,0 điểm).1. Phân tích đa thức thành nhân tử.2. Giải phương trình: Bài 3 (2,0 điểm. Cho biểu thức: (với x 0; x ≠ 1)a. Rút gọn biểu thức A.b. Tìm x để Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC 8cm, BH 2cm.a. Tính độ dài các đoạn thẳng AB, AC, AH.b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK BH.BC.c. Chứng minh...
Đọc tiếp
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
2. Giải phương trình:
Bài 3 (2,0 điểm. Cho biểu thức:
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 - 3(x + y) + 1993. Tính giá trị biểu thức P với:
a: \(=9-4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=9-4=5\)
b: \(=\sqrt{5}-2-\dfrac{1}{2}\cdot2\sqrt{5}=-2\)
Đúng 1
Bình luận (0)