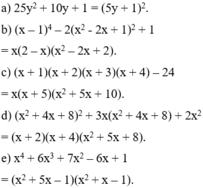phân tích đa thức thành nhân tử : a) x^2+6x-5 b) x^8+x+1 c) x^10+x^2+1

Những câu hỏi liên quan
bài 1: Phân tích đa thức thành nhân tử : x^2-6x+8
bài 2: Phân tích đa thức thành nhân tử : x^8+x^7+1
Bài 1 :
\(x^2-6x+8=x^2-2x-4x+8=x\left(x-2\right)-4\left(x-2\right)=\left(x-4\right)\left(x-2\right)\)
Bài 2 :
\(x^8+x^7+1=x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1-x^6-x^5-x^4-x^3-x^2-x\)
\(=x^6\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)+x^2+x+1-x^4\left(x^2+x+1\right)-x\left(x^2+x+1\right)\)
=\(\left(x^2+x+1\right)\left(x^6+x^3+1-x^4-x\right)\)
Tick đúng nha
Đúng 0
Bình luận (0)
Câu 1: Phân tích đa thức thành nhân tử
a. 6x² - 3xy
b. x2 -y2 - 6x + 9
c. x2 + 5x - 6
Câu 2 thực hiện phép tính
a. x + 2² - x - 3 (x + 1)
b. x³ - 2x² + 5x - 10 : ( x - 2)
Câu 3 Cho biểu thức A (x - 5) / (x - 4) và B (x + 5)/ 2x - (x - 6) / (5 - x) - (2x² - 2x - 50) / (2x² - 10x) (điều kiện x khác 0, x khác 4, x khác 5
a. Tính giá trị của A khi x² - 3x 0
b. Rút gọn B
c. Tìm giá trị nguyên của x để A : B có giá trị nguyên
Câu 4: Cho tam giác ABC cân tại A đường cao AD, O là trung đi...
Đọc tiếp
Câu 1: Phân tích đa thức thành nhân tử
a. 6x² - 3xy
b. x2 -y2 - 6x + 9
c. x2 + 5x - 6
Câu 2 thực hiện phép tính
a. x + 2² - x - 3 (x + 1)
b. x³ - 2x² + 5x - 10 : ( x - 2)
Câu 3 Cho biểu thức A = (x - 5) / (x - 4) và B = (x + 5)/ 2x - (x - 6) / (5 - x) - (2x² - 2x - 50) / (2x² - 10x) (điều kiện x khác 0, x khác 4, x khác 5
a. Tính giá trị của A khi x² - 3x = 0
b. Rút gọn B
c. Tìm giá trị nguyên của x để A : B có giá trị nguyên
Câu 4: Cho tam giác ABC cân tại A đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua cạnh OA.
a. Chứng minh tứ giác ADCE là hình chữ nhật
b. Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE
c. cho AB = 10 cm BC = 12 cm. Tính diện tích tam giác OAB
cíu tớ với
Phân tích đa thức thành nhân tử:a) 25
y
2
+ 10
y
8
+1;b)
(
x
-
1
)
4
-
2
(
x
2
-
2...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) 25 y 2 + 10 y 8 +1;
b) ( x - 1 ) 4 - 2 ( x 2 - 2 x + 1 ) 2 +1;
c) (x + 1)(x + 2)(x + 3)(x + 4) - 24;
d) ( x 2 + 4 x + 8 ) 2 + 3 x ( x 2 + 4x + 8) + 2 x 2 ;
e) x 4 + 6 x 3 +7 x 2 -6x + 1.
phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử
a 4x^3 - 13 x^2 + 9x - 18
b - x^3 - 6x^2 + 6x +1
c x^3 - 4x^2 - 8x + 8
a. \(=4x^3-12x^2-x^2+3x+6x-18=\left(x-3\right)\left(4x^2-x+6\right)\)
b. \(=-x^3+x^2-7x^2+7x-x+1=\left(x-1\right)\left(-x^2-7x-1\right)\)
c. \(=x^3+2x^2-6x^2-12x+4x+8=\left(x+2\right)\left(x^2-6x+4\right)\)
Đúng 0
Bình luận (0)
a) 3xy+6y
b) 3x2+9x
c) 6x-9y2
d) 10xy2-6x2y
Bài 2: Phân tích đa thức thành nhân tử
a) x(x-1)+5(x-1)
b) 3x(x+1)+3(x+1)
c) x(x-3)+xy(x-3)
d) 2x(x-2)-6(x-2)
Bài 1 yêu cầu gì em?
Bài 2:
\(a,x\left(x-1\right)+5\left(x-1\right)=\left(x+5\right)\left(x-1\right)\\ b,3x\left(x+1\right)+3\left(x+1\right)=\left(3x+3\right)\left(x+1\right)=3\left(x+1\right)\left(x+1\right)=3\left(x+1\right)^2\\ c,x\left(x-3\right)+xy\left(x-3\right)=\left(x+xy\right)\left(x-3\right)=x\left(y+1\right)\left(x-3\right)\\ d,2x\left(x-2\right)-6\left(x-2\right)=\left(2x-6\right)\left(x-2\right)=2\left(x-3\right)\left(x-2\right)\)
Đúng 2
Bình luận (0)
Bài 1:
a) \(3xy+6y\)
\(=3y\left(x+2\right)\)
b) \(3x^2+9x\)
\(=3x\left(x+3\right)\)
c) \(6x-9y^2\)
\(=3\left(2x-3y^2\right)\)
d) \(10xy^2-6x^2y\)
\(=2xy\left(5y-3x\right)\)
Bài 2:
a) \(x\left(x-1\right)+5\left(x-1\right)\)
\(=\left(x-1\right)\left(x+5\right)\)
b) \(3x\left(x+1\right)+3\left(x+1\right)\)
\(=\left(x+1\right)\left(3x+3\right)\)
\(=3\left(x+1\right)\left(x+1\right)\)
\(=3\left(x+1\right)^2\)
c) \(x\left(x-3\right)+xy\left(x-3\right)\)
\(=\left(x+xy\right)\left(x-3\right)\)
\(=x\left(1+y\right)\left(x-3\right)\)
d) \(2x\left(x-2\right)-6\left(x-2\right)\)
\(=\left(2x-6\right)\left(x-2\right)\)
\(=2\left(x-3\right)\left(x-2\right)\)
Đúng 1
Bình luận (0)
Bài `1`
`a,3xy +6y`
`= 3y(x+2)`
`b,3x^2+9x`
`= 3x(x+3)`
`c,6x-9y^2`
`= 3(2x- 3y^2)`
`d,10xy^2-6x^2y`
`= 2xy(5y-3x)`
Đúng 0
Bình luận (0)
1) Phân tích đa thức thành nhân tử ( = cách nhẩm nghiệm và hệ số bất định)
a) x^4+6x^3+11x^2+6x+1
b)x^4+7x^3+14x^2+14x+4
c)x^4-1ox^3-15x^2+20x+4
2)phân tích đa thức thành nhân tử( = cách hệ số bất định)
a) x^4-8x^3+11x^2+8x+12
b) x^4+x^2+1
c)x^4+4
1:Phân tích đa thức 5x+ 10 thành nhân tu 2: Giá trị của biểu thức x2 + 4x + 4 tại x 8 3: Phân tích đa thức x2 - 6x + 9 thành nhân tử 4:Một mảnh đất hình chữ nhật có chiều dài là ( x + 5 ) (m) và có chiều rộng là ( x - 5 ) (m) . Hỏi chiều dài của mảnh đất là bao nhiêu biết mảnh đất có diện tích là 24 m2 .
Đọc tiếp
1:Phân tích đa thức 5x+ 10 thành nhân tu
2: Giá trị của biểu thức x2 + 4x + 4 tại x= 8
3: Phân tích đa thức x2 - 6x + 9 thành nhân tử
4:Một mảnh đất hình chữ nhật có chiều dài là ( x + 5 ) (m) và có chiều rộng là ( x - 5 ) (m) . Hỏi chiều dài của mảnh đất là bao nhiêu biết mảnh đất có diện tích là 24 m2 .
Bài 1:
$5x+10=5(x+2)$
Bài 2:
Tại $x=8$ thì $x^2+4x+4=(x+2)^2=(8+2)^2=10^2=100$
Đúng 0
Bình luận (0)
Bài 3:
$x^2-6x+9=x^2-2.3.x+3^2=(x-3)^2$
Bài 4:
Diện tích mảnh đất là:
$(x+5)(x-5)=24$
$\Leftrightarrow x^2-25=24$
$\Leftrightarrow x^2=49$
$\Rightarrow x=7$ (do $x>5$)
Chiều dài mảnh đất là: $x+5=7+5=12$ (m)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a,2x^2-7x+6
b,x^2+x-6
c,x^3+3x^2+6x+4
d,x^10+x^5+1
e,(12x^2-12xy+3y^2)-10x(2x-y)
a,2x2-7x+6=(2x2-4x)-(3x-6)
=2x(x-3)-3(x-2)=(x-2)(2x-3)
b,x2+x-6=(x2+3x)-(2x+6)
=x(x-3)-2(x-3)=(x-3)(x-2)
c,x3+3x2+6x+4=x3+x2+2x2+2x+4x+4
=(x+1)(x2+2x+4)
d,x10+x5+1=(x10-x)+(x5-x2)+(x2+x+1)
=x((x3)3-1)+x2(x3-1)+(x2+x+1)
=x(x3-1)(x6+x3+1)+x2(x-1)(x2+x+1)+(x2+x+1)
=x(x-1)(x2+x+1)+x2(x-1)(x2+x+1)+(x2+x+1)
(x2+x+1)(x2-x+x3-x2+1)
e,(12x2-12xy+3y2)-10x(2x-y)=3(4x2-4xy+y2)-10x(2x-y)
=3(2x-y)2-10x(2x-y)=(2x-y)(6x-3y-10x)=(2x-y)(-4x-3y)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a,2x^2-7x+6
b,x^2+x-6
c,x^3+3x^2+6x+4
d,x^10+x^5+1
e,(12x^2-12xy+3y^2)-10x(2x-y)
Đúng 0
Bình luận (0)
\(2x^2-7x+6\)
\(=2x^2-3x-4x+6\)
\(=x\left(2x-3\right)-2\left(2x-3\right)\)
\(=\left(x-2\right)\left(2x-3\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a) 4x (a-b) +6xy(b-a)
b) (6x+3) - ( 2x-5) (2x+1)
c) 4 ( x-3)^2 +2x (3-x)
d) x^4 +2x^2 -4x-4
e) 2x (x+y) -x -y
g)( 3x-1 )^2 - (x+3)^2
a) \(4x\left(a-b\right)+6xy\left(b-a\right)\)
\(=4x\left(a-b\right)-6xy\left(a-b\right)\)
\(=\left(4x-6xy\right)\left(a-b\right)\)
\(=2x\left(2-3y\right)\left(a-b\right)\)
Đúng 1
Bình luận (0)
b) \(\left(6x+3\right)-\left(2x-5\right)\left(2x+1\right)\)
\(=3\left(2x+1\right)-\left(2x-5\right)\left(2x+1\right)\)
\(=\left(3-2x+5\right)\left(2x+1\right)\)
\(=\left(8-2x\right)\left(2x+1\right)\)
\(=2\left(4-x\right)\left(2x+1\right)\)
Đúng 1
Bình luận (0)
g: \(\left(3x-1\right)^2-\left(x+3\right)^2\)
\(=\left(3x-1-x-3\right)\left(3x-1+x+3\right)\)
\(=\left(2x-4\right)\left(4x+2\right)\)
\(=4\left(x-2\right)\left(2x+1\right)\)
Đúng 0
Bình luận (0)