Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm cho ở Bảng 17 (làm tròn kết quả đến hàng phần mười).
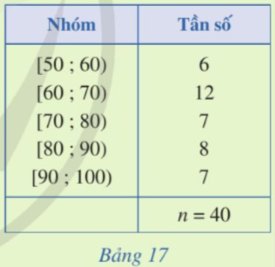
Tuổi các học viên của một lớp học Tiếng Anh tại một trung tâm được ghi lại ở bảng tần số ghép lớp như sau:
Lớp |
Tần số |
[16; 20) [20; 24) [24; 28) [28; 32) [32; 36) |
10 12 14 9 5 |
Khi đó độ lệch chuẩn của bảng số liệu là (kết quả làm tròn đến hàng phần chục):
A. 24,8
B. 5,3
C. 5,0
D. 25,0
Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập ![]() (vào chế thống kê).
(vào chế thống kê).
+ Nhập ![]() (hiển thị cột tần số).
(hiển thị cột tần số).
+ Nhập ![]() (nhập giá trị).
(nhập giá trị).
+ Nhập ![]() (nhập tần số), sau đó ấn
(nhập tần số), sau đó ấn ![]() .
.
+ Nhập ![]()
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.
Hai xạ thủ cùng tập bắn, mỗi người đã bắn 30 viên đạn vào bia. Kết quả được ghi lại ở các bảng sau.
Điểm số của xạ thủ A (Bảng 13)

Điểm số của xạ thủ B (Bảng 14)

Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê cho ở bảng 13, bảng 14.
Điểm số của xạ thủ A có:
x ≈ 8 , 3 đ i ể m , s 1 2 ≈ 1 , 6 ; s 1 ≈ 1 , 27 .
Điểm số của xạ thủ B có
y ≈ 8 , 4 đ i ể m , s 2 2 ≈ 1 , 77 ; s 2 ≈ 1 , 27 .
Cho bảng số liệu.
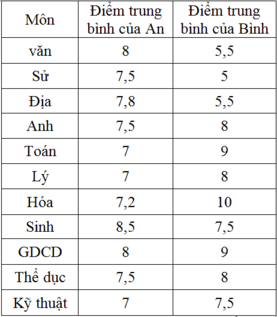
Tính phương sai và độ lệch chuẩn của Bình là:
A. 1,96 và 1,39
B. 1,92 và 1,38
C. 1,3 và 1,69
D. 1,38 và 1,13
Chọn B.
Phương sai và độ lệch chuẩn của Bình là:
Ta có 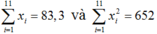
nên 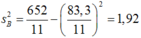
![]()
Cho bảng số liệu:
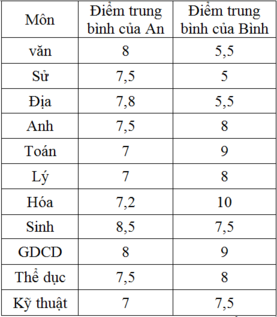
Tính phương sai và độ lệch chuẩn của An là:
A. 0,22 và 0,47
B. 0,2 và 0,41
C. 0,21 và 0, 48
D. 0,32 và 0,96
Chọn A.
Phương sai và độ lệch chuẩn của An:
Ta có 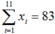 và
và 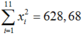
nên 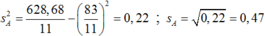
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
1.Làm tròn số 92,117 đến hàng phần mười được kết quả là:92,1
2.Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:-845,7
3.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
4.Làm tròn số 82,572 đến hàng phần mười được kết quả là:82,6
5.Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là:-72,9
\(92,117\approx92,12\\ -845,654\approx-845,65\approx-845,7\\ 82,572\approx82,57\\ 82,572\approx82,57\\ -72,882\approx-72,9\)
Tính phương sai và độ lệch chuẩn của dãy số liệu về chiều cao của học sinh nam và các học sinh nữ cho ở bảng 5
Dãy các số liệu chiều cao của các học sinh nam cho ở bảng 5 có
x 1 ≈ 163 ( c m ) ; s 1 2 ≈ 134 , 3 ; s 1 ≈ 11 , 59
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có
x 2 ≈ 159 , 5 ( c m ) ; s 2 2 ≈ 148 ; s 2 ≈ 12 , 17
Làm tròn số 92,117 đến hàng phần mười được kết quả là:
Làm tròn số -845,654 đến hàng phần mười (đến chữ số thập phân thứ nhất) được kết quả là:
Làm tròn số 82,572 đến hàng phần mười được kết quả :
Làm tròn số -72,882 đến chữ số thập phân thứ nhất được kết quả là
Làm tròn số -7671,08 đến hàng chục được kết quả là
Làm tròn số 86427 đến hàng trăm được kết quả là:
Làm tròn số 28,1 đến hàng đơn vị được kết quả là:
Làm tròn số -28,7 đến hàng đơn vị được kết quả là
Làm tròn số 128,5 đến hàng chục được kết quả là:
Làm tròn số 28,23 đến hàng đơn vị được kết quả là:
Làm tròn số 5960,12 đến hàng trăm được kết quả là
Làm tròn số -2367,785 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số 327,7892 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -29670 đến hàng nghìn được kết quả là:
Làm tròn số 7476,5 đến hàng đơn vị được kết quả là
Làm tròn số 4568,12 đến hàng trăm được kết quả là:
Làm tròn số -28,39 đến hàng phần mười được kết quả là:
Làm tròn số -67,193 đến chữ số thập phân thứ hai được kết quả là:
Làm tròn số -18,119 đến chữ số thập phân thứ hai được kết quả là
Làm tròn số -15427,99 đến hàng trăm được kết quả là:
Cho các số liệu thống kê ghi ở bảng sau
Số người xem trong 60 buổi chiếu phim của một rạp chiếu phim nhỏ
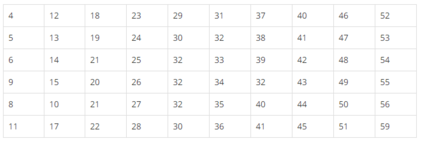
Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê đã cho
x ≈ 32 n g ư ờ i , s 2 ≈ 219 , 5 ; s ≈ 15 n g ư ờ i
Cho bảng phân bố tần số ghép lớp
Cân nặng của các học sinh lớp 10A và 10B, trường Trung học phổ thông L. (Bảng 17)
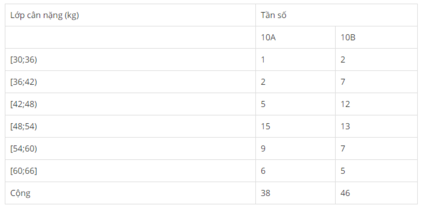
Tính số trung bình, độ lệch chuẩn của cá số liệu thống kê ở lớp 10A, lớp 10B.
Học sinh ở lớp 10A hay lớp 10B có khối lượng lớn hơn?
Ở lớp 10A, ta tính được
x 1 = 52 , 4 k g ; s 1 = 7 , 1 k g
Ở lớp 10B, ta tính được
x 2 = 49 k g ; s 2 = 7 , 9 k g
x 1 > x 2 , nên học sinh ở lớp 10A có khối lượng lớn hơn.
Em hãy tìm hiểu chiều cao của tất cả các bạn trong tổ và lập mẫu số liệu với kết quả tăng dần. Với mẫu số liệu đó, hãy tìm:
a) Số trung bình cộng, trung vị và tứ phân vị;
b) Khoảng biến thiên và khoảng tứ phân vị;
c) Phương sai và độ lệch chuẩn.
Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)