Trò chơi “Ghép thẻ”
a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:
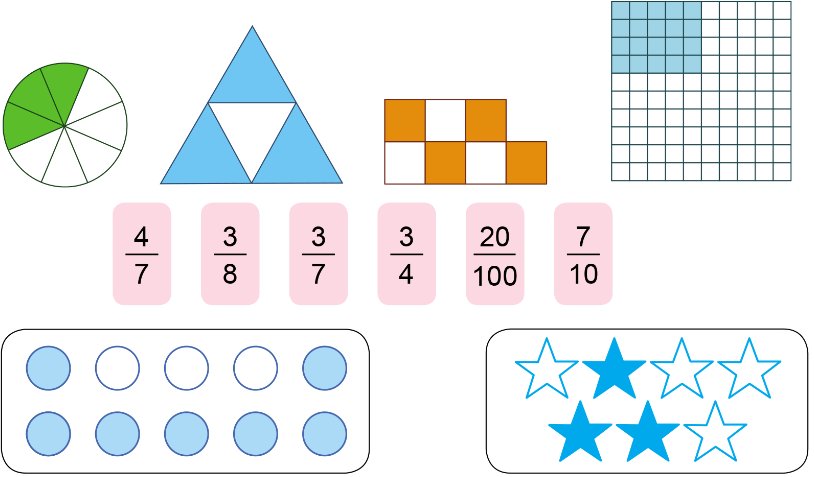
b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.
a) Chỉ ra phép tính có kết quả sai và sửa lại cho đúng:
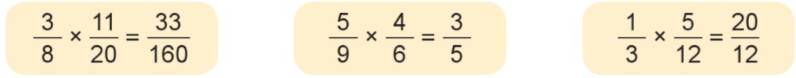
b) Ghép thẻ ghi phép nhân phân số với thẻ hình và thẻ ghi kết quả thích hợp:
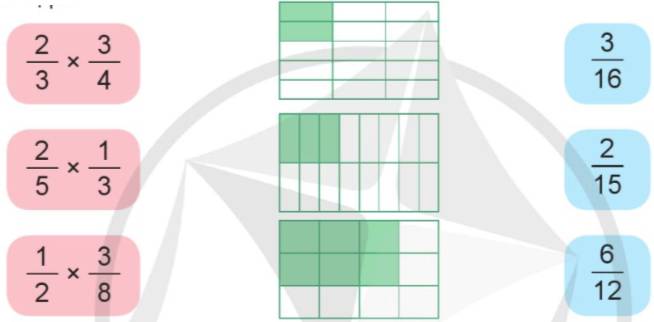
a: \(\dfrac{5}{9}\cdot\dfrac{4}{6}=\dfrac{5\cdot4}{9\cdot6}=\dfrac{20}{54}=\dfrac{10}{27}\)
\(\dfrac{1}{3}\cdot\dfrac{5}{12}=\dfrac{1\cdot5}{3\cdot12}=\dfrac{5}{36}\)
b:
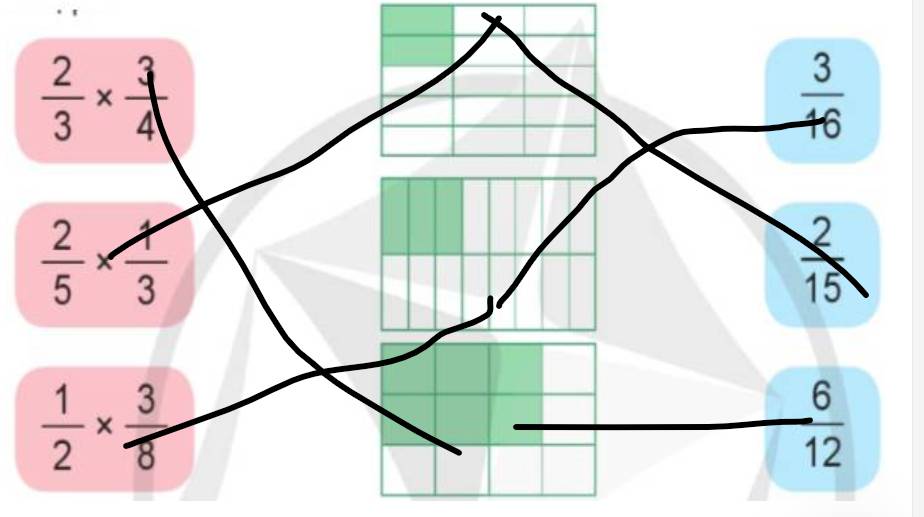
a,tìm ví dụ minh họa tính chất cơ bản của phân số
b,chơi trò chơi "ghép thẻ" : ghép các phân số vào nhau
thẻ : 1 phần 2
thẻ : 2 phần 5
thẻ : 3 phần 4
thẻ : 1 phần 3
các phân số đã cho : 4 phần 10, 4 phần 15, 6 phâng 12, 12 phần 16, 9 phần 15
mik mong các bạn hiểu .-.
giúp mình pls
Từ một hộp chứa 10 cái thẻ, trong đó các thẻ đánh số 1, 2, 3, 4, 5 màu đỏ, thẻ đánh số 6 màu xanh và các thẻ đánh số 7, 8, 9, 10 màu trắng. Lấy ngẫu nhiên một thẻ.
a.Mô tả không gian mẫu.
b.Kí hiệu A, B, C là các biến cố sau:
A: "Lấy được thẻ màu đỏ"
B: "Lấy được thẻ màu trắng"
C: "Lấy được thẻ ghi số chắn".
Hãy biểu diễn các biến cố A, B, C bởi các tập hợp con tương ứng của không gian mẫu.
a. Không gian mẫu gồm 10 phần tử:
Ω = {1, 2, 3, …, 10}
b. A, B, C "là các biến cố".
+ A: "Lấy được thẻ màu đỏ"
⇒ A = {1, 2, 3, 4, 5}
+ B: "Lấy được thẻ màu trắng"
⇒ B = {7, 8, 9, 10}
+ C: "Lấy được thẻ ghi số chắn".
⇒ C = {2, 4, 6, 8, 10}
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên đồng thời 2 chiếc thẻ từ trong hộp.
a) Gọi \(\Omega \) là không gian mẫu trong trò chơi trên. Tính số phần tử của tập hợp \(\Omega \).
b) Tính xác suất của biến cố “Tích các số trên hai thẻ là số lẻ”.
a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 5 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_5^2\) ( phần tử)
b)
+) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
+) Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 3 phần tử: \(n\left( A \right) = C_3^2\) ( phần tử)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_3^2}}{{C_5^2}} = \frac{3}{{10}}\)
a) Xếp các thẻ ghi phân số vào vị trí thích hợp trên tia số:
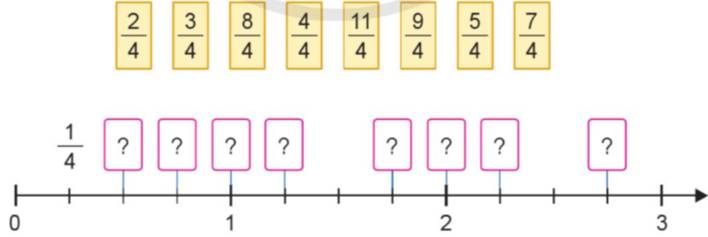
b) Trong các phân số ở câu a, phân số nào bé hơn 1? Phân số nào lớn hơn 1?
a) Xếp các thẻ ghi phân số vào vị trí thích hợp trên tia số
b) Áp dụng phương pháp so sánh phân số với 1
+ Nếu tử số bé hơn mẫu số thì phân số bé hơn 1
+ Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1
a) Xếp các thẻ ghi phân số vào vị trí thích hợp trên tia số
b) Áp dụng phương pháp so sánh phân số với 1
+ Nếu tử số bé hơn mẫu số thì phân số bé hơn 1
+ Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1
Một hộp đựng 10 tấm thẻ phân biệt gồm 6 tấm thẻ ghi số 1 và 4 tấm thẻ ghi số 0. Một trò chơi được thực hiện bằng cách rút ngẫu nhiên một thẻ từ hộp rồi hoàn lại. Sau một số lần rút, trò chơi sẽ kết thúc khi có đúng 3 lần rút được thẻ ghi số 1 hoặc hoặc đúng 3 lần thẻ ghi số 0. Tính xác suất để trò chơi kết thúc khi có đúng 3 lần rút được thẻ ghi số 1.
A. 0,9072
B. 0,33696
C. 0,456
D. 0,68256
trên bàn có 5 tấm thẻ , trên đó ghi các số 6 , 14 , 15 , 25 và 35 ( trên mỗi thẻ ghi mỗi số). Hai bạn Hùng và Yến , mỗi bạn lấy 2 trong 5 tấm thẻ đó. Biết rằng , tích các số ghi trên 2 tấm thẻ, mà mỗi bạn đã lấy là như nhau. Hỏi ở tấm thẻ còn lại là số mấy ?
Ta có: 35 * 6 = 210 = 15 * 14
==> Tấm thẻ còn lại là số 25
Bài giải
Tấm thẻ còn lại là:
6x35=15x14=210
\(\Rightarrow\)Tấm thẻ còn lại là số 25.
195 nha bn
chuc bn hoc tot nhe!
Viết rồi đọc các phân số chỉ phần đã tô mỗi màu trong mỗi hình. Với mỗi phân số, mẫu số cho biết gì, tử số chỉ gì?

Hình A:
Phân số: $\frac{3}{{21}}$
Đọc là: ba phần hai mươi mốt
Mẫu số 21 cho biết hình A được chia làm 21 phần bằng nhau. Tử số 3 cho biết có 3 phần như thế được tô màu.
Hình B:
Phân số: $\frac{6}{{21}}$
Đọc là: Sáu phần hai mươi mốt
Mẫu số 21 cho biết hình B được chia làm 21 phần bằng nhau. Tử số 6 cho biết có 6 phần như thế được tô màu.
Hình C:
Phân số: $\frac{{12}}{{21}}$
Đọc là: Mười hai phần hai mươi mốt
Mẫu số 21 cho biết hình C được chia làm 21 phần bằng nhau. Tử số 12 cho biết có 12 phần như thế được tô màu.
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tìm số phần tử của tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có một chữ số”;
b) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1”;
c) “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 4”.
Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ rút ra là: B = {1, 2, 3, …, 51, 52}.
Số phần tử của B là 52.
a) Có chín kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có một chữ số” là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Vì thế, xác suất của biến cố trên là: \(\dfrac{9}{{52}}\)
b) Có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1” là: 1, 21, 41.
Vì thế, xác suất của biến cố trên là: \(\dfrac{3}{{52}}\)
c) Ta có: \(4 = 0 + 4 = 1 + 3 = 2 + 2\)
Có năm kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 4” là: 4, 13, 22, 31, 40.
Vì thế, xác suất của biến cố trên là: \(\dfrac{5}{{52}}\)
a) Ghép ba thẻ số dưới đây được các số có ba chữ số nào?

b) Tìm số lớn nhất và số bé nhất trong các số có ba chữ số ghép được ở câu a.
a) Từ ba tấm thẻ ghi các số 40, và 5, ta lập được tất cả các số có ba chữ số như sau:
405 ; 450 ; 504 ; 540.
b) So sánh các số lập được ở câu a ta có:
405 < 450 < 504 < 540.
Vậy trong các số lập được, số lớn nhất là 540, số bé nhất là 405.