Giải phương trình:
x2-5x+36=8\sqrt{3x+4}
Giải phương trình:
x2+4x+7=(x+4)\(\sqrt{x^2+7}\)
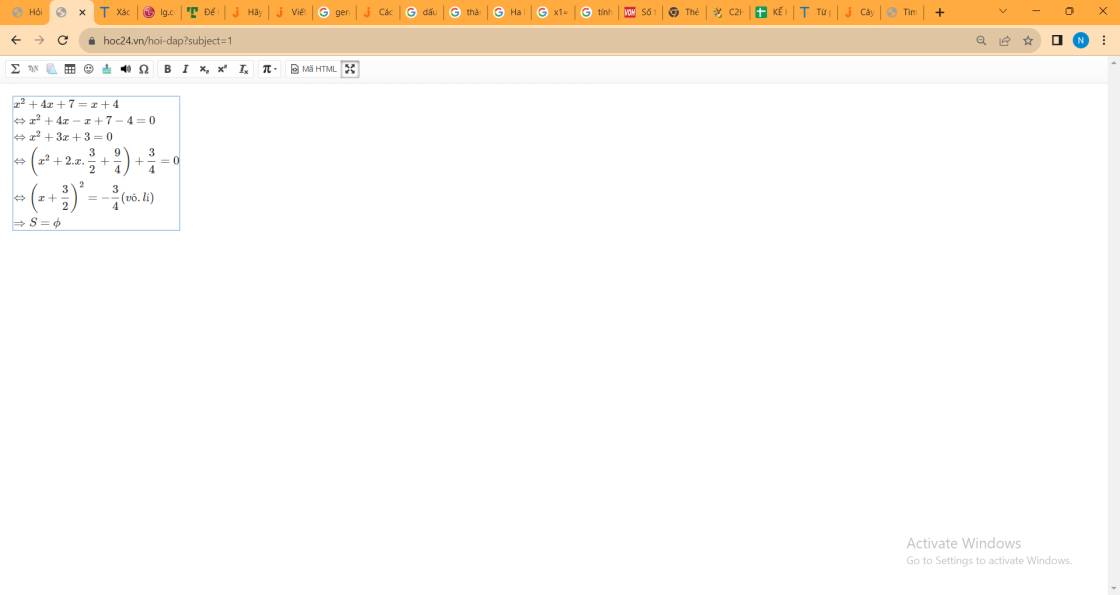
\(x^2+4x+7=x+4\\ \Leftrightarrow x^2+4x-x+7-4=0\\ \Leftrightarrow x^2+3x+3=0\\ \Leftrightarrow\left(x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}\right)+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{3}{4}\left(vô.lí\right)\\ \Rightarrow S=\phi\)
Bị lỗi hiển thị em hi
Em xem ha
giải pt: \(x^2-5x+36=8\sqrt{3x+4}.\)
\(x^2-5x+36=8\sqrt{3x+4}\)
\(\Leftrightarrow x^2-5x+36-8\sqrt{3x+4}=0\)
\(\Leftrightarrow\left(-8\sqrt{3x+4}+32\right)+\left(x^2-5x+4\right)=0\)
\(\Leftrightarrow-8\left(\sqrt{3x+4}-4\right)+\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow-8.\frac{3x+4-16}{\sqrt{3x+4}+4}+\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow-8.\frac{3x-12}{\sqrt{3x+4}+4}+\left(x-1\right)\left(x-4\right)=0\)
\(\left(x-4\right)\left(\frac{-24}{\sqrt{3x+4}+4}+x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\\frac{-24}{\sqrt{3x+4}+4}+x-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\-\frac{24}{\sqrt{3x+4}+4}+3+x-4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\-3.\frac{16-3x-4}{\left(\sqrt{3x+4}+4\right)^2}+\left(x-4\right)=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\\left(x-4\right)\left[\frac{9}{\left(\sqrt{3x+4}+4\right)^2}+1\right]=0\end{cases}}\)
Mà \(\frac{9}{\left(\sqrt{3x+4}+4\right)^2}+1>0\forall x\) nên \(x-4=0\Rightarrow x=4\)
Vật PT có nghiệm duy nhất là \(x=4\)
\(x^2-5x+36=\sqrt{3x+4}\)
giải phương trình này ạ,e cần trợ giúp
giải phương trình
a, \(\sqrt{1+x}-\sqrt{8-x}+\sqrt{\left(1+x\right)\left(8-x\right)}=3\)
b, \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
c, \(2x^2+4x=\sqrt{\dfrac{x+3}{2}}\)
d, \(2\left(x^2-3x+2\right)=3\sqrt{x^3+8}\)
e, \(729x^4+8\sqrt{1-x^2}=36\)
f, \(7x^2-10x+14=5\sqrt{x^4+4}\)
g, \(x^3+3x^2-3\sqrt[3]{3x+5}=1-3x\)
h, \(\sqrt{4-3\sqrt{10-3x}}=x-2\)
i, \(\sqrt{x-1}+\sqrt{x^2-1}=\sqrt{x^2-5x+4}\)
a) \(\sqrt{1+x}-\sqrt{8-x}+\sqrt{\left(1+x\right)\left(8-x\right)}=3\)
đặt t \(=\sqrt{1+x}-\sqrt{8-x}\)
\(\Leftrightarrow t^2=1+x-2\sqrt{\left(1+x\right)\left(8-x\right)}+8-x\)
\(\Leftrightarrow\sqrt{\left(1+x\right)\left(8-x\right)}=\dfrac{9-t^2}{2}\)
pt \(\Rightarrow t+\dfrac{9-t^2}{2}=3\)
\(\Leftrightarrow t^2-2t-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{1+x}-\sqrt{8-x}=-1\\\sqrt{1+x}-\sqrt{8+x}=3\end{matrix}\right.\)
suy ra tìm đc x
câu b đặt t =\(3x^2+5x+8\)
ta có pt \(\Leftrightarrow\sqrt{t}-\sqrt{t-7}=1\)
\(\Rightarrow t=16\)
\(\Leftrightarrow3x^2+5x+8=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{8}{3}\end{matrix}\right.\)
Giải các phương trình sau:
1) \(\sqrt{2x+4}-2\sqrt{2-x}=\dfrac{12x-8}{\sqrt{9x^2+16}}.\)
2) \(\sqrt{3x^2-7x+3}-\sqrt{x^2-2}=\sqrt{3x^2-5x-1}-\sqrt{x^2-3x+4}.\)
\(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
\(729x^4+8\sqrt{1-x^2}=36\)
Giải phương trình:
\(\sqrt{3x^2+6x+12}+\sqrt{5x^4-10x^2+30}=8\)
\(VT=\sqrt{3\left(x^2+2x+1\right)+9}+\sqrt{5\left(x^2-2x+1\right)+25}\ge\sqrt{9}+\sqrt{25}=8\)
Do dấu "=" ko đồng thời xảy ra ở hai bđt nên pt vô nghiệm
\(\sqrt{3\left(x+1\right)^2+9}-3+\sqrt{5\left(x^2-1\right)^2+25}-5=0\)
\(\Leftrightarrow\frac{3\left(x+1\right)^2}{\sqrt{3\left(x+2\right)^2+9}+3}+\frac{5\left(x+1\right)^2\left(x-1\right)^2}{\sqrt{5\left(x^2-1\right)^2+25}+5}=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(\frac{3}{\sqrt{3\left(x+2\right)^2+9}+3}+\frac{5\left(x-1\right)^2}{\sqrt{5\left(x^2-1\right)^2+25}+5}\right)=0\)
\(\left(\frac{3}{\sqrt{3\left(x+2\right)^2+9}+3}+\frac{5\left(x-1\right)^2}{\sqrt{5\left(x^2-1\right)^2+25}+5}\right)>0\left(\forall x\right)\)
\(\Rightarrow x=-1\)
Bạn kia làm sai rùi ạ chắc nhìn nhầm đề
Giải bất phương trình:
x2 - 2x + 8 < 0
\(x^2-2x+8< 0\)
\(\Leftrightarrow x^2-2x+1+7< 0\)
\(\Leftrightarrow\left(x-1\right)^2+7< 0\)
PTVN.
`x^2 - 2x + 8 < 0`
`<=> (x-1)^2 + 7 < 0`
`<=> (x-1)^2 < -7`
Vì `(x-1)^2 > -7` với mọi `x`
`=>` vô nghiệm
Vậy `x \in RR`
Giải hệ phương trình:
x2+5y24xy+6x-16y+12=0 và x+\(\sqrt{y-3}\) = 3