Cái đoạn áp dụng bất đẳng thức cosi cho 3 số rồi suy ra nó lớn hơn hoặc bằng 9 em không hiểu lắm ạ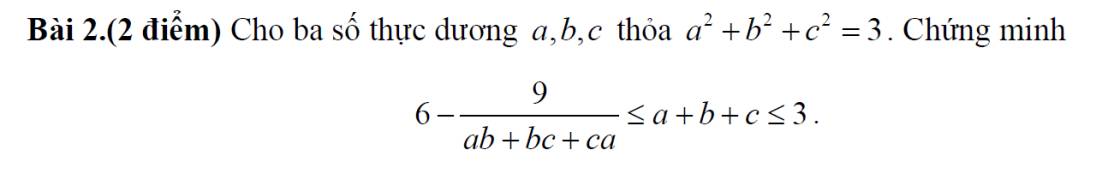


Những câu hỏi liên quan
chứng minh (a/c)+(a/b)+(b/c)+(b/a)+(c/a)+(c/b) lớn hơn hoặc bằng 6 (không áp dụng bất đẳng thức cosi)
Xem chi tiết
tìm Max
E = x + \(\sqrt{5-x^2}\) với -\(\sqrt{5}\) bé hơn hoặc bằng x bé hơn hoặc bằng \(\sqrt{5}\)
mn giúp mình cái này với bất đẳng thức bunhia cốp xki , mình cảm ơn ạ! ( mn nhớ giải thích trước khi áp dụng nhé)
- Áp dụng Bất Đẳng Thức Cosi để tìm giá trị lớn nhất, nhỏ nhất của:
\(\frac{3x-x^2-18}{x-2}\)
- Áp dụng Bất Đẳng Thức Cosi để tìm giá trị lớn nhất, nhỏ nhất của:
\(\frac{3x-x^2-18}{x-2}\)
bạn nói với mình điều kiện x>2 vậy làm như sau:
Đặt:\(A=\frac{3x-x^2-18}{x-2}=-\frac{x^2-3x+18}{x-2}=-\frac{x^2-4x+4+x-2+16}{x-2}\)
\(=-\frac{\left(x-2\right)^2+\left(x-2\right)+16}{x-2}\)\(=-\left(x-2+1+\frac{16}{x-2}\right)\)
Áp dụng bđt Cô si cho 2 số dương ta được: \(x-2+\frac{16}{x-2}\ge2\sqrt{\left(x-2\right).\frac{16}{x-2}}=8\)
=>\(x-2+\frac{16}{x-2}+1\ge9\)=>\(A=-\left(x-2+1+\frac{16}{x-2}\right)\le-9\)
=> maxA=-9 <=> x=6
Đúng 0
Bình luận (0)
Có bạn nào biết làm bài này ko ạ. Nếu biết thì giúp mình nhanh nhanh nhé, mình cảm ơn nhiều lắm
Bài 1: Áp dụng bất đẳng thức Cô Si chứng minh :
a) x/y + y/x lớn hơn hoặc bằng 2, với x, y>0
b) Cho a,b, c >0 ; a+b+c=1
Chứng minh 1/a + 1/b + 1/c lớn hơn hoặc bằng 9
a) áp dụng bđt cô si cho 2 số ta có
\(\dfrac{x}{y}+\dfrac{y}{x}\ge2\sqrt{\dfrac{x}{y}.\dfrac{y}{x}}\)
⇔ \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\) (đpcm )
b) áp dụng bđt cô si dạng phân số ta có
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}\)
⇔ \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge9\) (đpcm)
Đúng 0
Bình luận (0)
Với x,y,z dương. Không sử dụng bất đẳng thức Cosi. C/m biểu thức sau
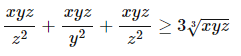
Cho a,b,c là các số dương t/m a+b+c=1 a/a+b² + b/b+c² + c/c+a² < hoặc = ¼(1/a + 1/b +1/c) sử dụng bất đẳng thức cosi
=>
=>
=>
Tương tự, ta có:
Do đó, ta có:
(ĐPCM)
Đúng 0
Bình luận (0)
Cho 2 số a,b không âm.Chứng minh
\(\frac{a+b}{2}\)\(\ge\)\(\sqrt{ab}\) ( Bất đẳng thức Cosi cho hai số không âm).
Dấu đẳng thức xảy ra khi nào ?
Chứng minh bằng biến đổi tương đương :
\(\frac{a+b}{2}\ge\sqrt{ab}\) \(\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge\) (luôn đúng)
Bđt cuối luôn đúng nên bđt ban đầu được chứng minh.
Dấu "=" xảy ra khi \(\sqrt{a}-\sqrt{b}=0\Leftrightarrow a=b\) (a,b không âm)
Đúng 0
Bình luận (0)
Áp dụng bất đẳng thức Cô-si cho hai số không âm, chứng minh: Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:
a + b 2 ≥ a b
Các hình chữ nhật có cùng chu vi thì a + b 2 không đổi. Từ bất đẳng thức a + b 2 ≥ a b và không đổi suy ra ab đạt giá trị lớn nhất bằng a + b 2 khi a = b.
Điều này cho thấy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Đúng 0
Bình luận (0)
Áp dụng bất đẳng thức bunhiacopxki ta có left(a+b+cright)^2geleft(1+1+1right)left(a^2+b^2+c^2right)ge9Rightarrow a+b+cge3Áp dụng bất đẳng thức cauchy-schwarz ta có: frac{1}{a}+frac{1}{b}+frac{1}{c}gefrac{9}{a+b+c}Rightarrow Pge2left(a+b+cright)+frac{9}{a+b+c}a+b+c+frac{9}{a+b+c}+a+b+cÁp dụng bất đẳng thức cosi ta có a+b+c+frac{9}{a+b+c}ge2sqrt{frac{left(a+b+cright).9}{a+b+c}}2sqrt{9}6Lại có a+b+cge3 (chứng minh trên)Rightarrow Pge6+39Vậy giá trị nhỏ nhất của P là 9. Dấu bằng xảy ra khi abc1
Đọc tiếp
Áp dụng bất đẳng thức bunhiacopxki ta có
\(\left(a+b+c\right)^2\ge\left(1+1+1\right)\left(a^2+b^2+c^2\right)\ge9\Rightarrow a+b+c\ge3\)
Áp dụng bất đẳng thức cauchy-schwarz ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\)
\(\Rightarrow P\ge2\left(a+b+c\right)+\frac{9}{a+b+c}=a+b+c+\frac{9}{a+b+c}+a+b+c\)
Áp dụng bất đẳng thức cosi ta có \(a+b+c+\frac{9}{a+b+c}\ge2\sqrt{\frac{\left(a+b+c\right).9}{a+b+c}}=2\sqrt{9}=6\)
Lại có \(a+b+c\ge3\) (chứng minh trên)
\(\Rightarrow P\ge6+3=9\)
Vậy giá trị nhỏ nhất của P là 9. Dấu bằng xảy ra khi a=b=c=1

















