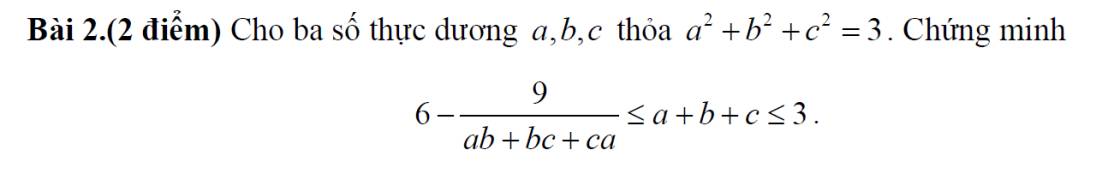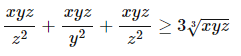Áp dụng BĐT Cô-si:
$a^2+b^2\geq 2ab; b^2+c^2\geq 2bc; c^2+a^2\geq 2ac$
$\Rightarrow 2(a^2+b^2+c^2)\geq 2(ab+bc+ac)$
$\Rightarrow a^2+b^2+c^2\geq ab+bc+ac$
$\Rightarrow (a+b+c)^2\geq 3(ab+bc+ac)$
Do đó:
$(a+b+c)+(a+b+c)+\frac{9}{ab+bc+ac}\geq 3\sqrt[3]{(a+b+c)(a+b+c).\frac{9}{ab+bc+ac}}=3\sqrt[3]{\frac{9(a+b+c)^2}{ab+bc+ac}}$
$\geq 3\sqrt[3]{\frac{9.3(ab+bc+ac)}{ab+bc+ac}}=3\sqrt[3]{27}=9$
Với x,y,z dương. Không sử dụng bất đẳng thức Cosi. C/m biểu thức sau
Cho a,b,c là các số dương t/m a+b+c=1 a/a+b² + b/b+c² + c/c+a² < hoặc = ¼(1/a + 1/b +1/c) sử dụng bất đẳng thức cosi
Áp dụng bất đẳng thức Cô-si cho hai số không âm, chứng minh: Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Áp dụng bất đẳng thức bunhiacopxki ta có
\(\left(a+b+c\right)^2\ge\left(1+1+1\right)\left(a^2+b^2+c^2\right)\ge9\Rightarrow a+b+c\ge3\)
Áp dụng bất đẳng thức cauchy-schwarz ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\)
\(\Rightarrow P\ge2\left(a+b+c\right)+\frac{9}{a+b+c}=a+b+c+\frac{9}{a+b+c}+a+b+c\)
Áp dụng bất đẳng thức cosi ta có \(a+b+c+\frac{9}{a+b+c}\ge2\sqrt{\frac{\left(a+b+c\right).9}{a+b+c}}=2\sqrt{9}=6\)
Lại có \(a+b+c\ge3\) (chứng minh trên)
\(\Rightarrow P\ge6+3=9\)
Vậy giá trị nhỏ nhất của P là 9. Dấu bằng xảy ra khi a=b=c=1
Áp dụng bất đẳng thức Cô-si cho ba số không âm, chứng minh: Trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.
Cho a lớn hơn hoặc bằng 0, b lớn hơn hoặc bằng 0 . Chứng minh bất đẳng thức Cauchy : \(\frac{a+b}{2}\)lớn hơn hoặc bằng \(\sqrt{ab}\)
chứng minh bất đẳng thức : ( a + 1 )2 lớn hơn hoặc bằng 4a
Chứng minh bất đẳng thức: a+ 1/a lớn hơn hoặc bằng 2 với a>0
Cho x+y+z=3 . Chứng minh bất đẳng thức
x2 +y2 +z2 +xy+xz+yz lớn hơn hoặc bằng 6
Tìm Max của \(A=4\sqrt{x-5}+7\sqrt{9-x}\) hấn không bao giờ tồn tại đúng không các bạn nó chỉ tồn tại Min thôi. Tuy áp dụng Bunhiacopsky rồi nhưng dấu bằng nó không xảy ra.
