1: Xét ΔABC vuôg tại A vàΔHBA vuông tại H có

góc B chung

=>ΔABC đồng dạng với ΔHBA

2: Xét ΔBKI vuông tại B và ΔABC vuông tại A có

góc BIK=góc ACB

=>ΔBKI đồng dạng vơi ΔABC

=>KI/BC=BI/AC

=>KI*AC=1/2BC^2

b: Sửa đề: AO vuông góc BI

Gọi M là trung điểm của IC

Xét ΔIHC có IO/IH=IM/IC

nên OM//HC và OM=1/2HC

=>OM vuông góc AH

Xet ΔAHM có

MO,HI là đường cao

MO cắt HI tại O

=>O là trực tâm

=>AO vuông góc HM

=>AO vuông góc BI

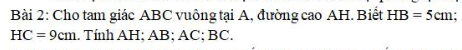
áp dụng HTL:

\(AH^2=BH\cdot HC\Leftrightarrow AH=\sqrt{BH\cdot HC}=\sqrt{5\cdot9}=3\sqrt{5}cm\)

\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(3\sqrt{5}\right)^2+5^2}=\sqrt{70}cm\left(Pytago\right)\)

\(AC=\sqrt{AH^2+HC^2}=\sqrt{\left(3\sqrt{5}\right)^2+9^2}=3\sqrt{14}cm\left(Pytago\right)\)

\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\sqrt{70}\right)^2+\left(3\sqrt{14}\right)^2}=14cm\left(Pytago\right)\)

\(BC=BH+HC=14\left(cm\right)\)

Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\sqrt{BH.HC}=3\sqrt{5}\left(cm\right)\\AB=\sqrt{BC.BH}=\sqrt{70}\left(cm\right)\\AC=\sqrt{BC.CH}=3\sqrt{14}\left(cm\right)\end{matrix}\right.\)

a: Xét ΔADM và ΔCBN có 

\(\widehat{ADM}=\widehat{CBN}\)

AD=BC

\(\widehat{DAM}=\widehat{BCN}\)

Do đó: ΔADM=ΔCBN

Suy ra: AM=CN

a: Xét ΔAOC và ΔBOC có

OA=OB

\(\widehat{AOC}=\widehat{BOC}\)

OC chung

DO đó: ΔAOC=ΔBOC

b: Xét tứ giác OAEB có 

C là trung điểm của OE

C là trung điểm của AB

Do đó: OAEB là hình bình hành

Suy ra: AE//OB