Ai giúp em câu 2 với ạ pls;-;

Giúp em câu 1b và câu 4 với ạ ,pls!!!!

1.
b, \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}+\dfrac{\sqrt{2}}{1-\sqrt{2}}\)
\(=\dfrac{2\left(2+\sqrt{2}\right)\left(3-\sqrt{2}\right)}{3-\sqrt{2}}-\dfrac{\sqrt{2}\left(\sqrt{2}+3\right)}{\sqrt{2}}+\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1-\sqrt{2}}\)
\(=4+2\sqrt{2}-\sqrt{2}-3-2-\sqrt{2}\)
\(=-1\)
Bài 1:
b: Ta có: \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}-\dfrac{\sqrt{2}}{\sqrt{2}-1}\)
\(=2\sqrt{2}\left(\sqrt{2}+1\right)-\sqrt{2}-3-2+\sqrt{2}\)
\(=4+2\sqrt{2}-5\)
\(=2\sqrt{2}-1\)
4.
a, ĐK: \(x\ge0;x\ne1\)
\(Q=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\dfrac{2\sqrt{x}}{\left(1-x\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(1-x\right)^2}{2}\)
\(=\dfrac{\sqrt{x}\left(1-\sqrt{x}\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-x\)
b, \(Q=\sqrt{x}-x=\sqrt{x}\left(1-\sqrt{x}\right)>0\)
\(\Leftrightarrow1-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)
Vậy \(0\le x< 1\)
c, \(Q=\sqrt{x}-x\)
\(=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(\Rightarrow maxQ=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{4}\)
ai làm hộ em câu hình này với ạ pls
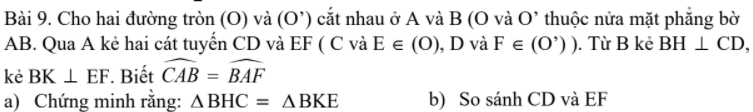
ai làm hộ 2 câu hình này với ạ pls

ai làm hộ em 2 câu này với pls
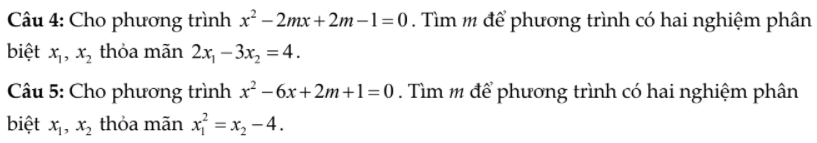
Bài 2 :
\(\Delta'=m^2-\left(2m-1\right)=\left(m-1\right)^2\ge0\)
Để pt có 2 nghiệm pb
\(m-1\ne0\Leftrightarrow m\ne1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)
Ta có : \(2x_1-3x_2=4\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=2m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=2m-\dfrac{4m-4}{5}=\dfrac{6m+4}{5}\end{matrix}\right.\)
Thay vào (3) ta được \(\left(\dfrac{6m+4}{5}\right)\left(\dfrac{4m+4}{5}\right)=2m-1\)
\(\Rightarrow\left(6m+4\right)\left(4m+4\right)=50m-25\Leftrightarrow24m^2+40m+16=50m-25\)
\(\Leftrightarrow24m^2-10m+41=0\)
\(\Delta'=10-41.24< 0\)Vậy pt vô nghiệm hay ko có gtri m
5.
\(\Delta'=9-\left(2m+1\right)=8-2m>0\Rightarrow m< 4\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2m+1\end{matrix}\right.\)
Kết hợp Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1^2=x_2-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2=6-x_1-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2+x_1-2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=1;x_2=5\\x_1=-2;x_2=8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m+1\Rightarrow\left[{}\begin{matrix}2m+1=5\\2m+1=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{17}{2}\end{matrix}\right.\) (thỏa mãn)
ai làm hộ em 2 câu hình này với pls

1.Is it okay if I bring a friend to the party?
2.The letters that people wrote after his death gave me a lot of comfort.
chuyển sang câu bị động giúp em với ạ chiều nay em nộp rồi, pls
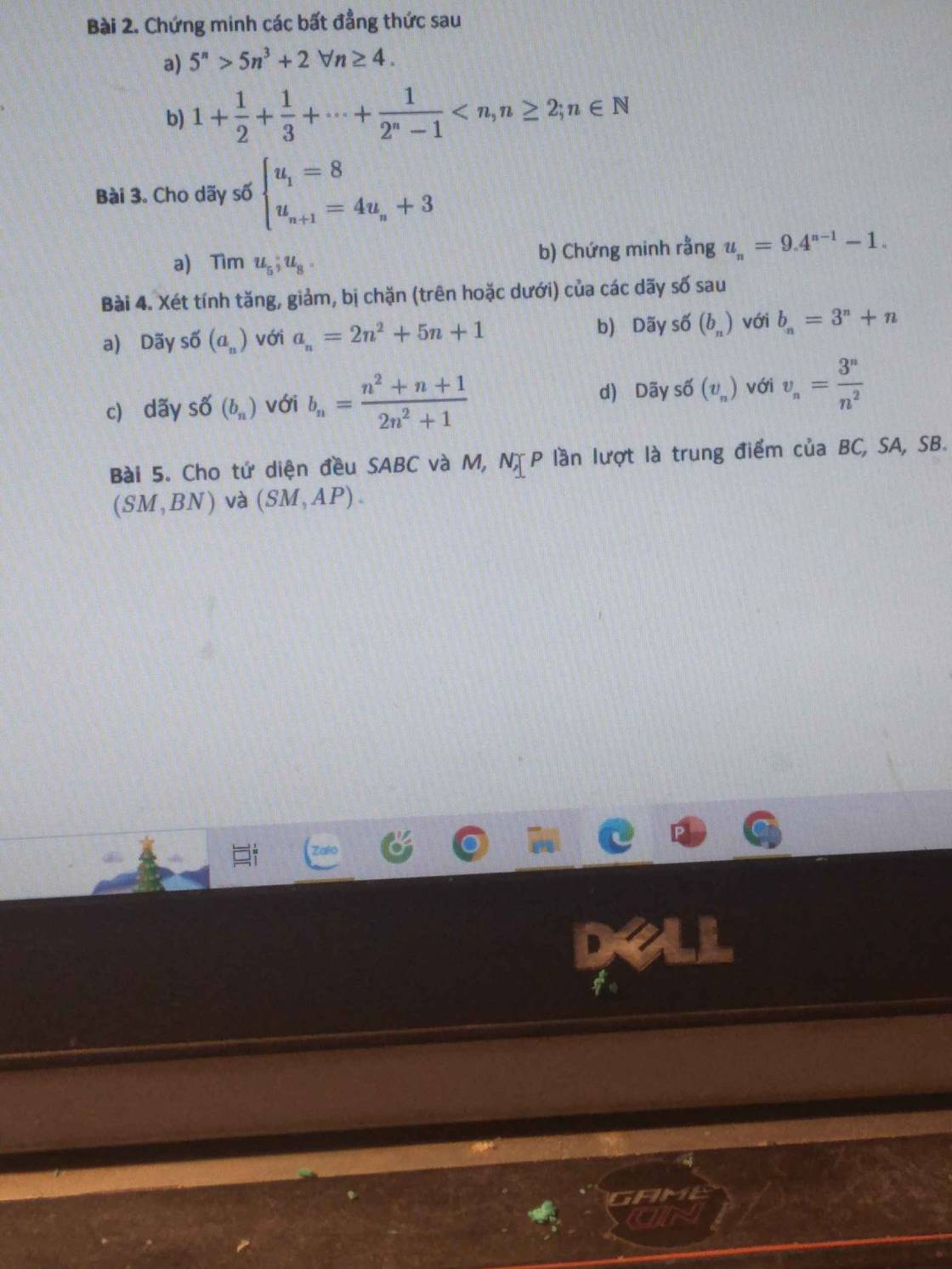 giúp em bài 4 với ạ. Pls
giúp em bài 4 với ạ. Pls
Từ câu chuyện "Bàn tay lạnh cóng" hãy viết 1 bài văn nghị luận trình bày suy nghĩ của em về câu chuyện trên?
Mọi người giúp mình với pls, mai thi rồi ạ :((
Ai giúp em câu 2 với ạ :(((
Lời giải:
$\overrightarrow{MA}=(1-x, 3-y), \overrightarrow{MB}=(4-x, 2-y)$
Để $MAB$ là tam giác vuông cân tại $M$ thì:
\(\left\{\begin{matrix}
\overrightarrow{MA}.\overrightarrow{MB}=0\\
MA^2=MB^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(1-x)(4-x)+(3-y)(2-y)=0\\
(1-x)^2+(3-y)^2=(4-x)^2+(2-y)^2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ 6x-2y-10=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ y=3x-5\end{matrix}\right.\)
\(\Leftrightarrow (x,y)=(2,1), (3,4)\)
Lm câu a) vs c) giúp mình với ạ mình cần gấp pls🙏
a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)