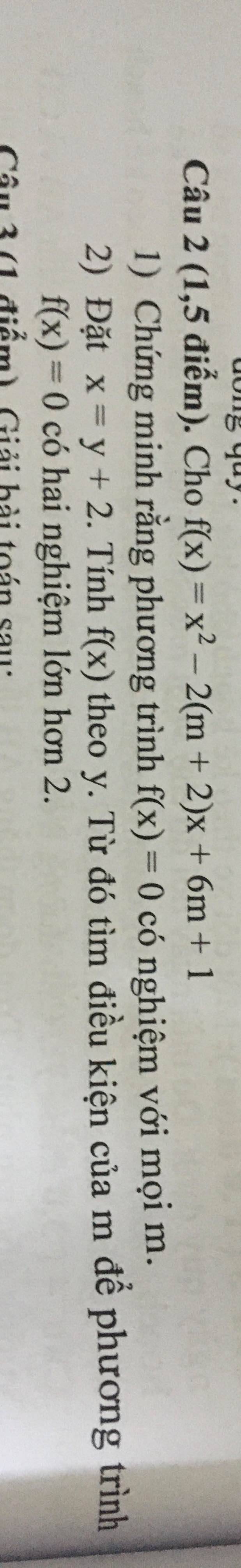Gi ải giúp mình vs ah
Gi ải giúp mình vs ah

Những câu hỏi liên quan
Giữ ải giúp mình câu hs này với ạ
1: \(F\left(x\right)=x^2-2\left(m+2\right)x+6m+1\)
Đặt F(x)=0
=>\(x^2-2\left(m+2\right)x+6m+1=0\)
=>\(x^2-\left(2m+4\right)x+6m+1=0\)
\(\Delta=\left(2m+4\right)^2-4\left(6m+1\right)\)
\(=4m^2+16m+16-24m-4\)
\(=4m^2-8m+12=4\left(m^2-2m+3\right)\)
\(=4\left(m^2-2m+1+2\right)\)
\(=4\left[\left(m-1\right)^2+2\right]>0\forall m\)
=>Phương trình F(x)=0 luôn có nghiệm với mọi m
2: \(f\left(x\right)=x^2-2\left(m+2\right)x+6m+1\)
\(=\left(y+2\right)^2-2\left(m+2\right)\left(y+2\right)+6m+1\)
\(=y^2+4y+4-2y\left(m+2\right)-4\left(m+2\right)+6m+1\)
\(=y^2+y\left(4-2m-4\right)+4-4m-8+6m+1\)
\(=y^2+\left(-2m\right)\cdot y+2m-3\)
Để phương trình f(x)=0 có hai nghiệm lớn hơn 2 thì phương trình f(y)=0 có hai nghiệm lớn hơn 0
Đặt f(y)=0
=>\(y^2+\left(-2m\right)\cdot y+2m-3=0\)
\(\Delta=\left(-2m\right)^2-4\left(2m-3\right)\)
\(=4m^2-8m+12=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\forall m\)
=>Phương trình f(y)=0 luôn có hai nghiệm phân biệt
Để phương trình f(y)=0 có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}y_1+y_2>0\\y_1\cdot y_2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{-\left(-2m\right)}{1}>0\\\dfrac{2m-3}{1}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m>0\\2m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m>0\\2m>3\end{matrix}\right.\Leftrightarrow2m>3\)
=>m>3/2
Đúng 1
Bình luận (0)
Giúp mình vs ah mình cảm ơn nhiều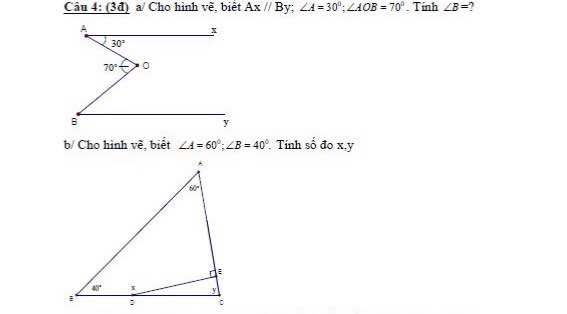
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
Đúng 1
Bình luận (0)
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
Đúng 1
Bình luận (0)
Câu 4b.
Xét tứ giác $ABDE$ có:
$\widehat{A}+\widehat{B}+\widehat{D}+\widehat{E}=360^0$ (tổng 4 góc trong tứ giác)
$60^0+40^0+x+90^0=360^0$
$\Rightarrow x=170^0$
$\widehat{EDC}=180^0-x=180^0-170^0=10^0$
Xét tam giác $EDC$ vuông tại $E$:
$\widehat{E}+\widehat{EDC}+\widehat{C}=180^0$
$90^0+10^0+y=180^0$
$\Rightarrow y=80^0$
Đúng 1
Bình luận (0)
Giúp mình vs ah
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 0
Bình luận (0)
giúp mình vs ah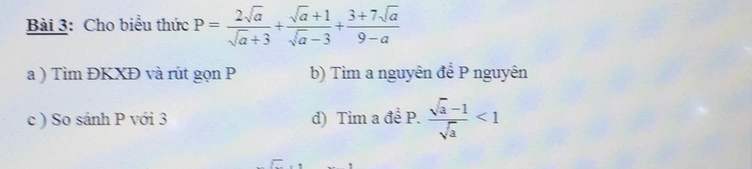
a, đkxđ : a >= 0 ; a khác 9
\(P=\dfrac{2\sqrt{a}\left(\sqrt{a}-3\right)+\left(\sqrt{a}+1\right)\left(\sqrt{a}+3\right)-3-7\sqrt{a}}{a-9}\)
\(=\dfrac{2a-6\sqrt{a}+a+4\sqrt{a}+3-3-7\sqrt{a}}{a-9}=\dfrac{3a-9\sqrt{a}}{a-9}=\dfrac{3\sqrt{a}}{\sqrt{a}+3}\)
b, \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}=\dfrac{3\left(\sqrt{a}+3\right)-9}{\sqrt{a}+3}=3-\dfrac{9}{\sqrt{a}+3}\Rightarrow\sqrt{a}+3\inƯ\left(9\right)=\left\{1;3;9\right\}\)
| \(\sqrt{a}+3\) | 1 | 3 | 9 |
| a | loại | 0 | 36 |
c, Ta có : \(3=\dfrac{3\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\)mà \(3\left(\sqrt{a}+3\right)>3\sqrt{a}\)
Vậy P < 3
d, Ta có : \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}.\dfrac{\sqrt{a}-1}{\sqrt{a}}< 1\Leftrightarrow\dfrac{3\left(\sqrt{a}-1\right)}{\sqrt{a}+3}-1< 0\)
\(\Leftrightarrow\dfrac{3\sqrt{a}-3-\sqrt{a}-6}{\sqrt{a}+3}< 0\Rightarrow2\sqrt{a}-9< 0\)vì \(\sqrt{a}+3>0\)
\(\Leftrightarrow\sqrt{a}< \dfrac{9}{2}\Leftrightarrow a< \dfrac{81}{4}\)
Kết hợp đk vậy \(0\le a< \dfrac{81}{4}\)
Đúng 2
Bình luận (0)
Giúp mình vs ah 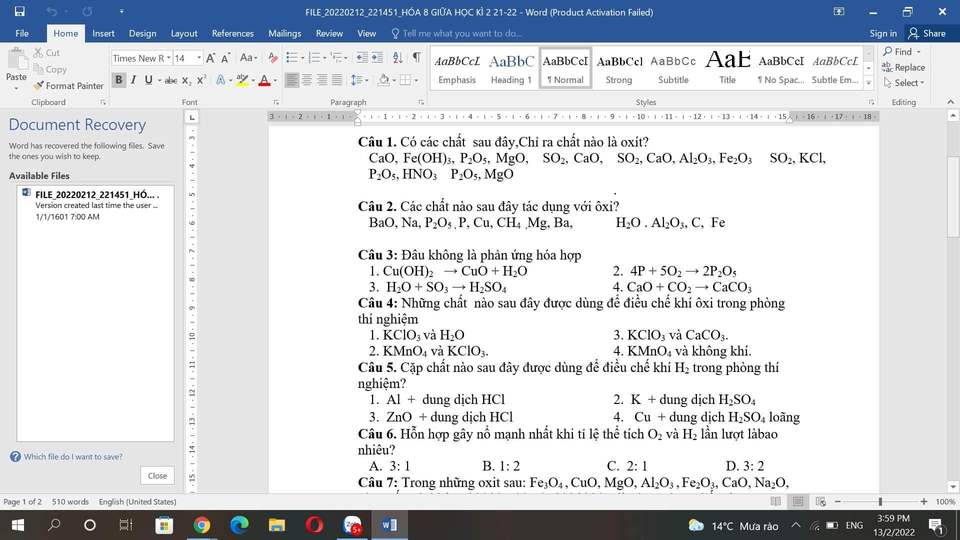
Anh nhớ em đăng 1 lần nhưng câu 1 câu 2 anh chả thấy có đánh số để chọn
Anh nhắm theo mắt anh nhé
Câu 1: Chọn nhóm SO2, CaO, Al2O3, Fe2O3
Câu 2: Na, P, Cu, CH4, Mg, Fe, C, Ba
Câu 3: 1
Câu 4: 2
Câu 5: 1
Câu 6: B
Đúng 1
Bình luận (0)
Giúp mình vs ah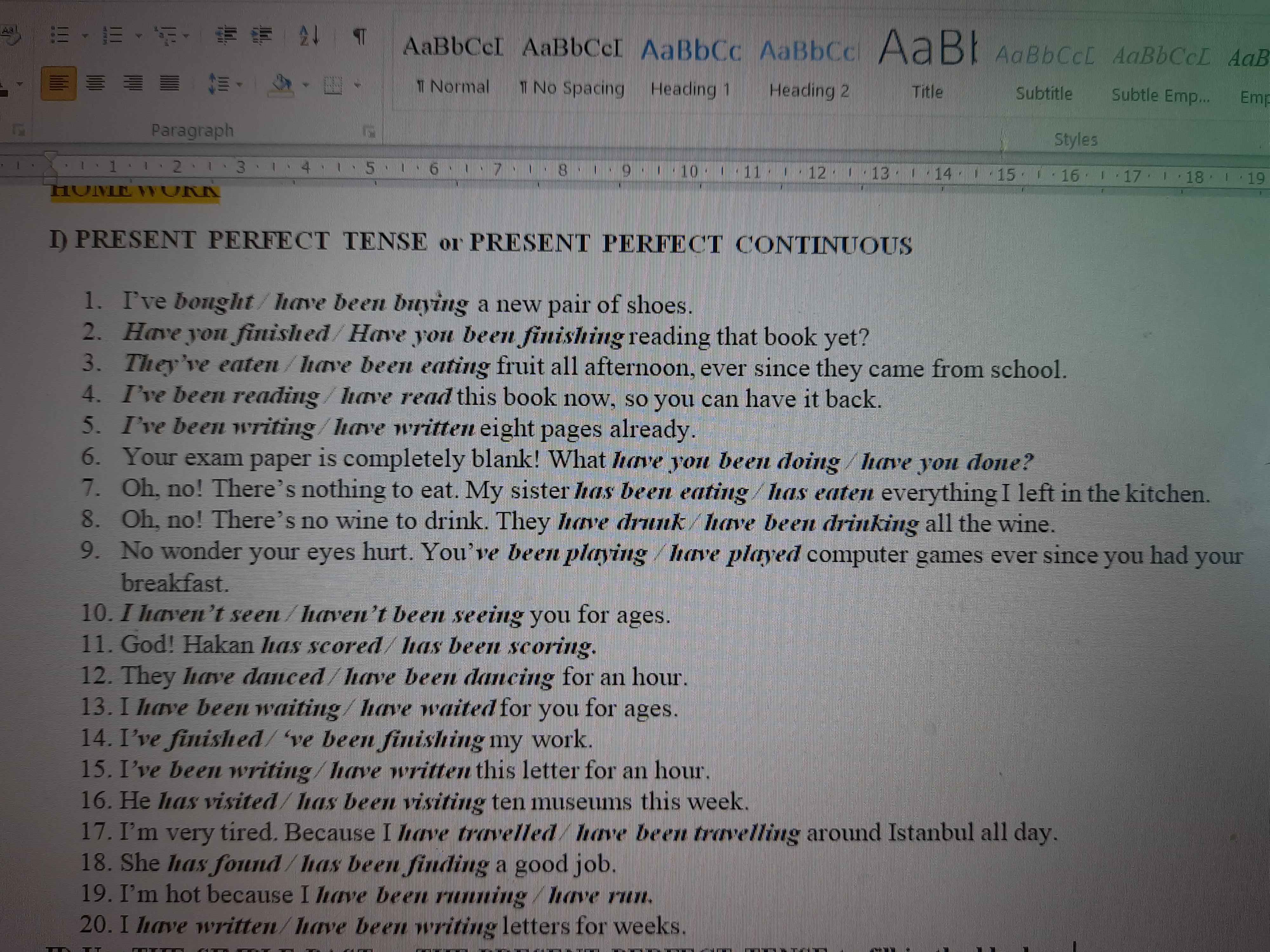
Học sớm zậy...
Me lớp 5 học chuyên mới học cái này ;-;
Đúng 0
Bình luận (0)
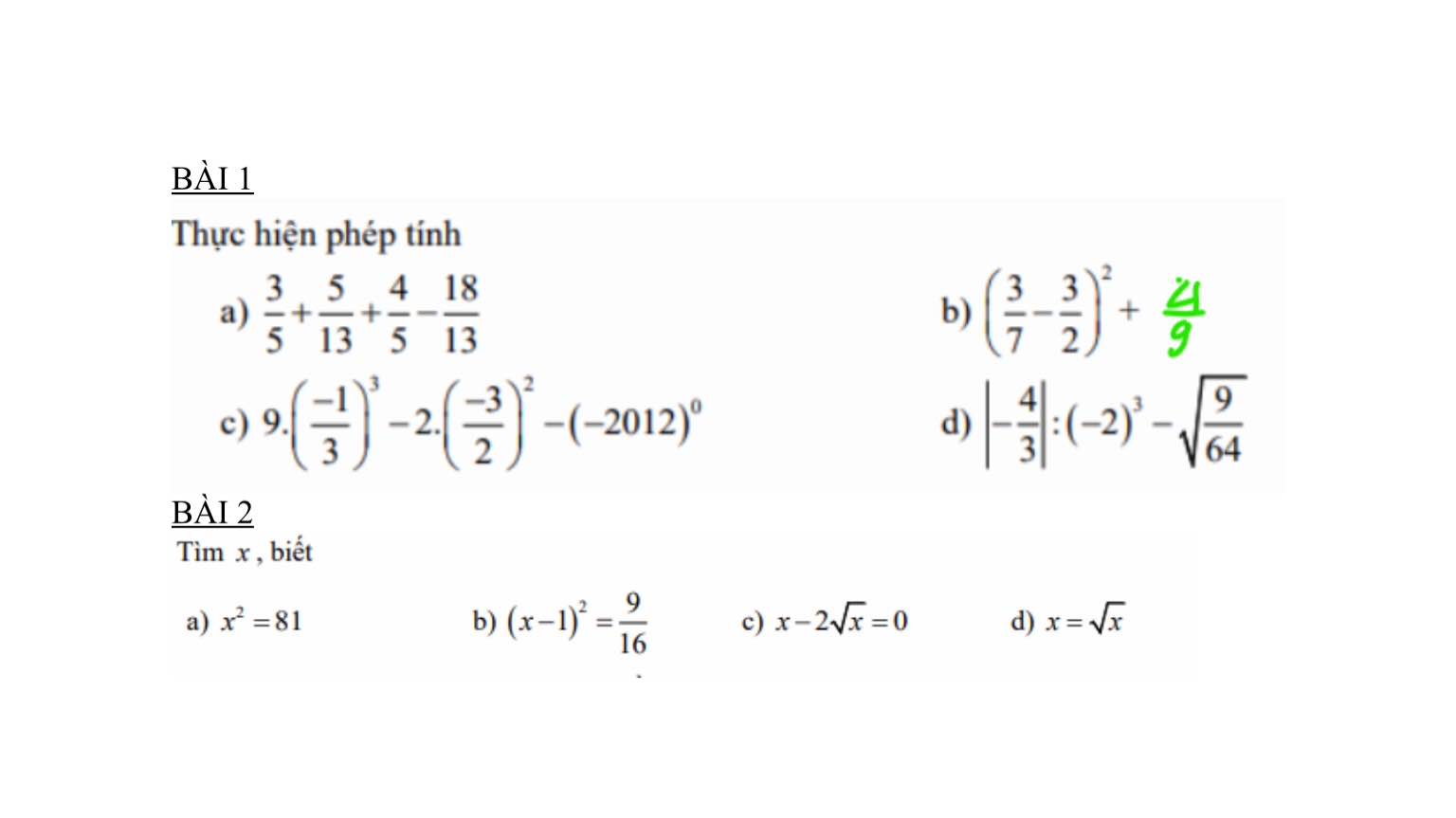 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!!
mn giúp mình vs ah
Các bạn giúp mình vs ah
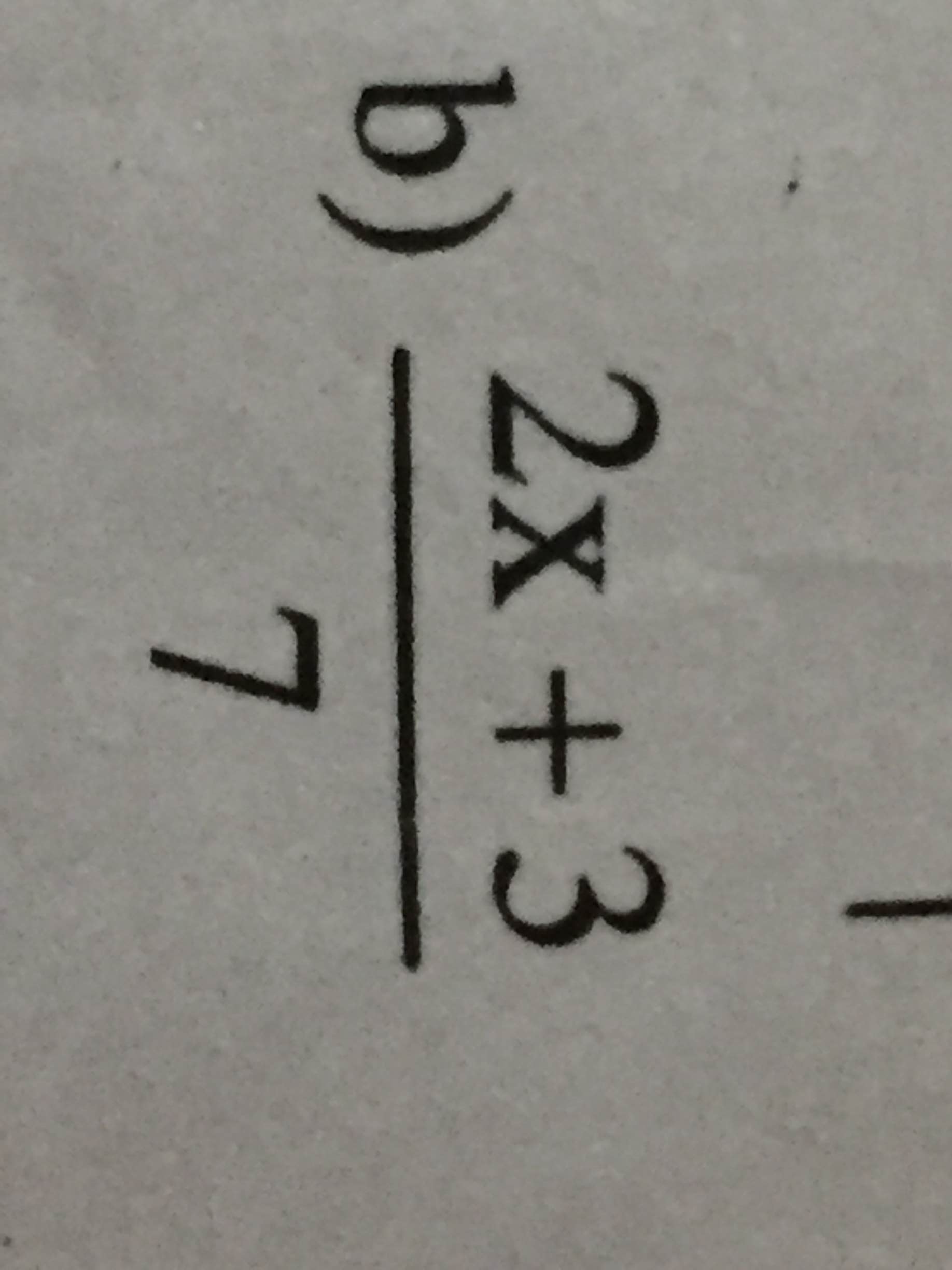
giúp mình vs gấp gấp ah
1: góc AHC+góc AKC=180 độ
=>AHCK nội tiếp
2: AHCK nội tiếp
=>góc AHK=góc ACK=1/2*sđ cung AC=góc ABC
Đúng 0
Bình luận (0)