1: \(F\left(x\right)=x^2-2\left(m+2\right)x+6m+1\)
Đặt F(x)=0
=>\(x^2-2\left(m+2\right)x+6m+1=0\)
=>\(x^2-\left(2m+4\right)x+6m+1=0\)
\(\Delta=\left(2m+4\right)^2-4\left(6m+1\right)\)
\(=4m^2+16m+16-24m-4\)
\(=4m^2-8m+12=4\left(m^2-2m+3\right)\)
\(=4\left(m^2-2m+1+2\right)\)
\(=4\left[\left(m-1\right)^2+2\right]>0\forall m\)
=>Phương trình F(x)=0 luôn có nghiệm với mọi m
2: \(f\left(x\right)=x^2-2\left(m+2\right)x+6m+1\)
\(=\left(y+2\right)^2-2\left(m+2\right)\left(y+2\right)+6m+1\)
\(=y^2+4y+4-2y\left(m+2\right)-4\left(m+2\right)+6m+1\)
\(=y^2+y\left(4-2m-4\right)+4-4m-8+6m+1\)
\(=y^2+\left(-2m\right)\cdot y+2m-3\)
Để phương trình f(x)=0 có hai nghiệm lớn hơn 2 thì phương trình f(y)=0 có hai nghiệm lớn hơn 0
Đặt f(y)=0
=>\(y^2+\left(-2m\right)\cdot y+2m-3=0\)
\(\Delta=\left(-2m\right)^2-4\left(2m-3\right)\)
\(=4m^2-8m+12=4m^2-8m+4+8=\left(2m-2\right)^2+8>0\forall m\)
=>Phương trình f(y)=0 luôn có hai nghiệm phân biệt
Để phương trình f(y)=0 có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}y_1+y_2>0\\y_1\cdot y_2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{-\left(-2m\right)}{1}>0\\\dfrac{2m-3}{1}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m>0\\2m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m>0\\2m>3\end{matrix}\right.\Leftrightarrow2m>3\)
=>m>3/2
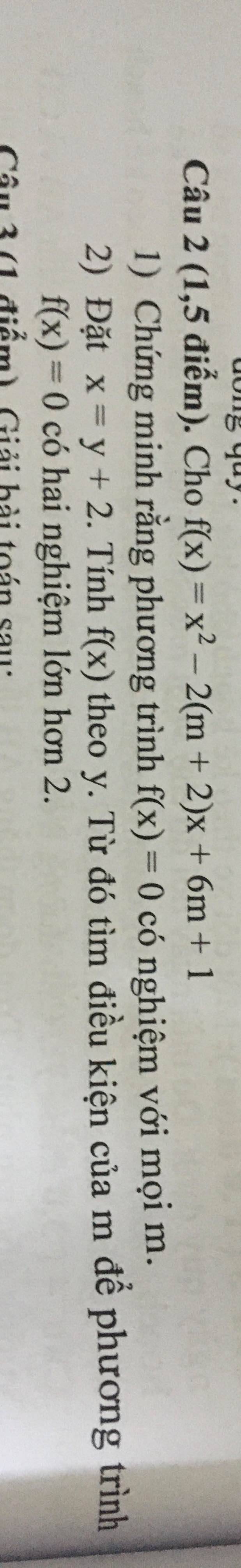
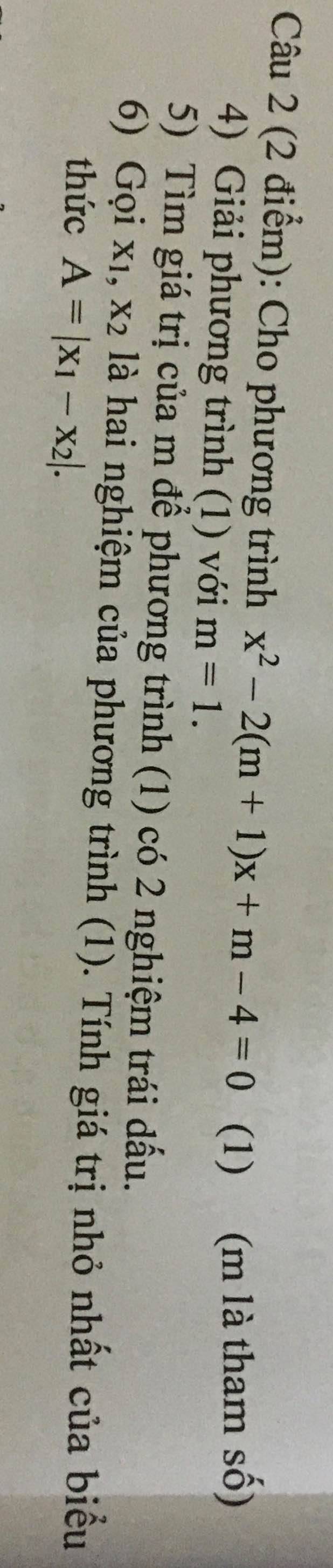
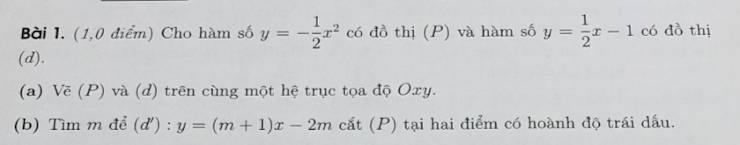giúp mình câu này với ạ
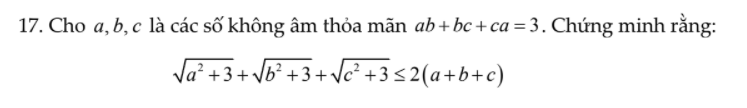câu này với ạ! Mình cảm ơn.