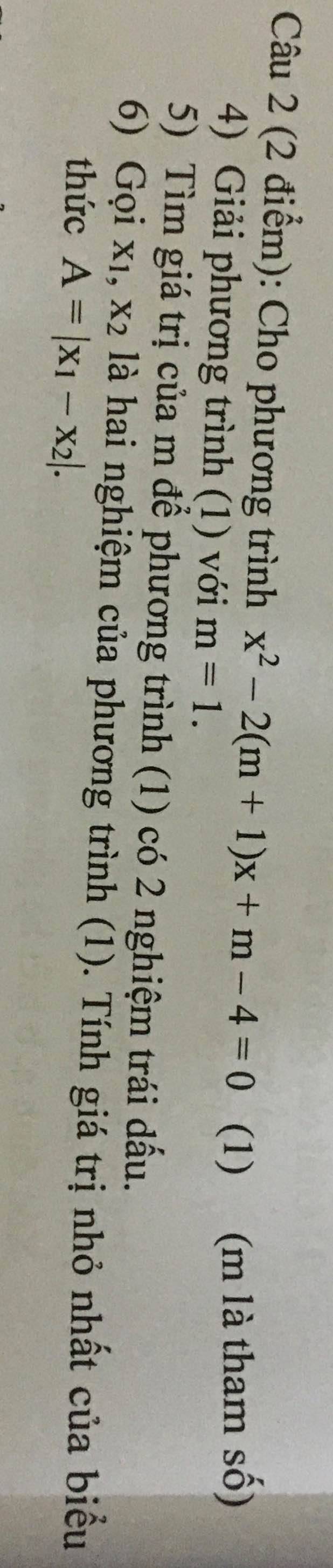4: \(x^2-2\left(m+1\right)x+m-4=0\left(1\right)\)
Thay m=1 vào phương trình (1), ta được:
\(x^2-2\cdot\left(1+1\right)x+1-4=0\)
=>\(x^2-4x-3=0\)
=>\(x^2-4x+4-7=0\)
=>\(\left(x-2\right)^2=7\)
=>\(x-2=\pm\sqrt{7}\)
=>\(x=2\pm\sqrt{7}\)
5: Để phương trình (1) có hai nghiệm trái dấu thì \(1\cdot\left(m-4\right)< 0\)
=>m-4<0
=>m<4
6: \(\text{Δ}=\left(-2m-2\right)^2-4\left(m-4\right)\)
\(=4m^2+8m+4-4m+16\)
\(=4m^2+4m+20\)
\(=4m^2+4m+1+19=\left(2m+1\right)^2+19>0\forall m\)
=>Phương trình (1) luôn có hai nghiệm phân biệt
Áp dụng định lí Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=2\left(m+1\right)\\x_1\cdot x_2=\dfrac{c}{a}=m-4\end{matrix}\right.\)
\(A=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(2m+2\right)^2-4\left(m-4\right)}\)
\(=\sqrt{4m^2+8m+4-4m+16}\)
\(=\sqrt{4m^2+4m+1+19}\)
\(=\sqrt{\left(2m+1\right)^2+19}>=\sqrt{19}\forall m\)
Dấu '=' xảy ra khi 2m+1=0
=>2m=-1
=>\(m=-\dfrac{1}{2}\)
Vậy: \(A_{min}=\sqrt{19}\) khi \(m=-\dfrac{1}{2}\)