Cho tam giác ABC gọi I là trung điểm của BC qua I kẻ đường thẳng d1 cắt AC tại M và cắt AB tại N và đường thẳng d2 cắt AC tại P và cắt AB tại Q đường thẳng PN cắt BC tại E đường thẳng QN cắt BC tại F chứng minh rằng IE=IF

Những câu hỏi liên quan
Cho tam giác ABC, I là trung điểm BC. Qua I kẻ đường thẳng d1 cắt AC,AB tại M,N và đường thẳng d2 cắt CA,AB tại P,Q ;PN cắt BC tại E; QM cắt BC tại F .Chứng minh: IE=IF
Cho tam giác ABC, I là trung điểm BC. Qua I kẻ đường thẳng d1 cắt AC,AB tại M,N và đường thẳng d2 cắt CA,AB tại P,Q ;PN cắt BC tại E; QM cắt BC tại F .Chứng minh: IE=IF
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABC
1 like
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABCgiúp đỡ nha mọi người
Đọc tiếp
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABC
giúp đỡ nha mọi người
bạn lm bài này ch. gửi cho mk cách lm vs
Đúng 0
Bình luận (2)
Cho ∆ABC, gọi I là trung điểm của BC. Qua I kẻ đường thẳng d1 cắt CA, AB lần lượt tại M, N và đường thẳng d2 cắt cạnh CA, AB lần lượt tại P, Q. Đường thẳng PN cắt cạnh BC tại E và đường thẳng QM cắt cạnh BC tại F.
Chứng minh IE= IF
Cho tam giác ABC nhọn (ABAC),nội tiếp đường tròn (O;R).Các tiếp tuyến tại B và C cắt nhau . Gọi H là giao điểm của OM và BC .Từ M kẻ đường thẳng song song với AC,đường thẳng song song cắt tại E và F (E thuộc cung nhỏ BC),cắt BC tại I ,cắt AB tại K.a)Chứng minh:MO⊥BC và ME.MFMH.MOb)Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp.Từ đó suy ra năm điểm M,B,K,O,C cùng thuộc một đường tròn.
Đọc tiếp
Cho tam giác ABC nhọn (AB>AC),nội tiếp đường tròn (O;R).Các tiếp tuyến tại B và C cắt nhau . Gọi H là giao điểm của OM và BC .Từ M kẻ đường thẳng song song với AC,đường thẳng song song cắt tại E và F (E thuộc cung nhỏ BC),cắt BC tại I ,cắt AB tại K.
a)Chứng minh:MO⊥BC và ME.MF=MH.MO
b)Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp.Từ đó suy ra năm điểm M,B,K,O,C cùng thuộc một đường tròn.
a: Xét (O) có
MB,MC là tiếp tuyến
=>MB=MC
mà OB=OC
nên OM là trung trực của BC
Xét ΔMEB và ΔMBF có
góc MBE=góc MFB
góc EMB chung
=>ΔMEB đồng dạng với ΔMBF
=>MB^2=ME*MF=MH*MO
Đúng 1
Bình luận (0)
Cho tam giác ABC ( AB<AC) , tia phân giác của góc A cắt cạnh BC tại D . Gọi M là trung điểm của cạnh BC, qua M kẻ đường thẳng // với AD, đường thẳng này cắt tia đối của AB tại E và cắt cạnh AC tại F. C/M: BE=FC
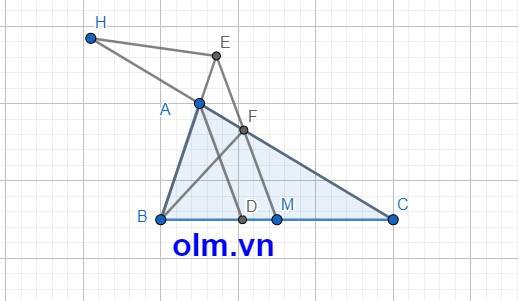
Kéo dài AC về phía A lấy điểm H sao cho CF = FH;
Lúc này bài toán trở thành chứng minh BE = HF
Xét tam giác HBC có: MB = MC (gt); FH = FC
Nên MF là đường trung bình của tam giác HBC ⇒ ME//BH
Mặt khác ta có ME//AD ⇒ \(\widehat{AEF}\) = \(\widehat{BAD}\) (hai góc đồng vị) (1)
\(\widehat{BAD}\) = \(\widehat{DAF}\) (AD là phân giác của góc BAC) (2)
\(\widehat{DAF}\) = \(\widehat{AFE}\) (hai góc so le trong) (3)
Kết hợp (1);(2);(3) ta có: \(\widehat{AEF}\) = \(\widehat{AFE}\) ⇒ \(\Delta\)AEF cân tại A ⇒ AE = AF (*)
Vì ME//HB nên: \(\widehat{AHB}\) = \(\widehat{AFE}\) (so le trong)
\(\widehat{ABH}\) = \(\widehat{AEF}\) (so le trong)
⇒ \(\widehat{AHB}\) = \(\widehat{ABH}\) ⇒ \(\Delta\) AHB cân tại A ⇒ AB = AH (**)
Cộng vế với vế của(*) và(*) ta có: AE + AB = AF + AH
⇒ BE = FH
⇒ BE = CF (vì cùng bằng HF)
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn (AB AC), nội tiếp đường tròn (O; R). Các tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường thẳng song song với AC, đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại Ka) Chứng minh: MO vuông góc BC và ME.MF MH.MOb) Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp. Từ đó suy ra 5 điểm M, B, K, O, C cùng thuộc một đường trònc) Đường thẳng OK cắt O tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt O tại Q...
Đọc tiếp
Cho tam giác ABC nhọn (AB > AC), nội tiếp đường tròn (O; R). Các tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường thẳng song song với AC, đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại K
a) Chứng minh: MO vuông góc BC và ME.MF = MH.MO
b) Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp. Từ đó suy ra 5 điểm M, B, K, O, C cùng thuộc một đường tròn
c) Đường thẳng OK cắt O tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt O tại Q (Q khác P). Chứng minh ba điểm M, N, Q thẳng hàng
1, Cho tam giác ABC có I là trung điểm của cạnh BC. Qua I kẻ đường thẳng d cắt AB,AC lần lượt tại M và N . Kẻ dường thẳng d' cắt AC,AB lần lượt tại E,F . CMR : IE=IF
2, cho hình thoi ABCD có góc B bằng 60 độ . Một đường thẳng đi qua D cắt đường kéo dài các cạnh AB,BC lần lượt tại E và F. Gọi M là giao điểm của AF, CE . Chứng minh rằng : AD^2 = AM.AF














