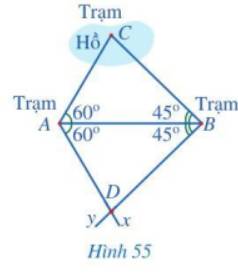
Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.

Vậy \(\Delta ABC = \Delta ABD\) (g.c.g). 

Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)

Độ cao các thửa ruộng so với mực nước biển tạo thành một cấp số cộng với số hạng đầu u₁ = 1 250 m và công sai d = 1,2 (m).

Khi đó công thức tổng quát của cấp số cộng là: un = u₁ + (n – 1).d = 1 250 + (n – 1).1,2.

Vậy độ cao của thửa ruộng thứ 10 so với mực nước biển là:

u₁₀ = 1 250 + (10 – 1).1,2 = 1 260,8 m.

Độ dài đèo Hải Vân là:

\(6,28:\frac{{157}}{{500}} = \frac{{157}}{{25}}.\frac{{500}}{{157}} = \frac{{3135}}{{157}} \approx 20\,\left( {km} \right)\)

Bạn ấy áp dụng hđt hiệu hai bình phương

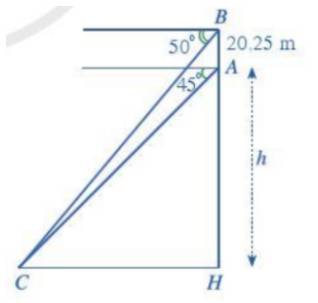
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)

Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)

Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)

\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)

Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).

Ta có:

\(\widehat B + 90^\circ  + 18^\circ  = 180^\circ \) (tổng ba góc của một tam giác).

Suy ra: \(\widehat B = 180^\circ  - 90^\circ  - 18^\circ  = 72^\circ \)

Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là 72°.

Ta có: \(f\left( t \right) = {f_1}\left( t \right) + {f_2}\left( t \right) = 5\sin t + 5\cos t = 5\left( {\sin t + \cos t} \right) = 5\sqrt 2 \sin \left( {t + \frac{\pi }{4}} \right)\)

Suy ra: \(k = 5\sqrt 2 ,\;\varphi  = \frac{\pi }{4}\).

Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega  \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).

Chữ đã viết trên tờ giấy ở hình bên là gì chữ “MẮT”.

Có hiện tượng trên là do chữ “MẮT” đặt trước gương sẽ cho ảnh ảo như trên.

- Cách 1:

Hàm số biểu diễn đồ thị \(y =  - 0,00188{\left( {x - 251,5} \right)^2} + 118\)

\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow  - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)

Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)

- Cách 2: 

Ta có phương trình thành cầu: \(y =  – 0,00188(x – 251,5)^2 + 118\)

\( \Leftrightarrow  y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai. 

Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I. 

Ta có: \(b = 0,94564, c = – 0,91423\)

\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I =  – 0,00188(x_I – 251,5)^2 + 118 =118.\)

Vậy độ cao lớn nhất cần tìm là 118 m.