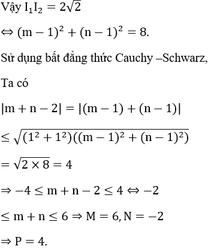Cho hai số m và n thoả mãn m > n. Chứng tỏ m + 5 > n + 4.

Những câu hỏi liên quan
Cho 2 số tự nhiên m và n thoả mãn (m+1)/n không bằng (n+1)/m nguyên. CMR: ƯCLN(m;n) không vượt quá căn bậc hai của m+n
cho các số nguyên dương m,n,k thoả mãn mn=k2 và ƯCLN(m,n,k)=1. chứng minh rằng: m,n là các số chính phương
ĐỀ SAI NHÉ,PHẢI LÀ (M,N)=1 THÔI
Dễ dàng CM được tính chất sau: 1 số chính phương chia hết cho số nguyên tố p thì chia hết cho \(p^2\)
Quay lại với bài này:
Đặt: \(\hept{\begin{cases}m=p_1.p_2...p_i\\n=q_1.q_2...q_j\end{cases}},p_k,q_l\)là các số nguyên tố và do (m,n)=1 => \(p_k\)bất kỳ khác \(q_l\)
Áp dụng trực tiếp tính chất trên ta => m,n là số chính phương
Đúng 0
Bình luận (0)
Xét tập (A) gồm các số phức z thoả mãn
z
-
2
i
z
-
2
là số thuần ảo và các giá trị thực m,n sao cho chỉ có duy nhất một số phức
z
∈
(
A
)
thoả mãn |z-m-ni|
2
. Đặt Mmax( m+n) và Nmin( m+n). Tính PM+N. A. P -2 B. P -4 C. P 4 D. P 2
Đọc tiếp
Xét tập (A) gồm các số phức z thoả mãn z - 2 i z - 2 là số thuần ảo và các giá trị thực m,n sao cho chỉ có duy nhất một số phức z ∈ ( A ) thoả mãn |z-m-ni|= 2 . Đặt M=max( m+n) và N=min( m+n). Tính P=M+N.
A. P = -2
B. P = -4
C. P = 4
D. P = 2
Cho hai số m và n nguyên dương và nguyên tố cùng nhau thoả mãn m+n=90. Tìm giá trị lớn nhất của m nhân n .
các bạn giúp mình với nhé
Lời giải:
Vì $m,n$ nguyên tố cùng nhau, $m+n=90$ chẵn nên $m,n$ là hai số lẻ phân biệt.
Không mất tổng quát giả sử $m>n$.
$90=m+n>2n\Rightarrow n< 45$. Vì $n$ lẻ nên $n\leq 43$.
Có:
$mn=(90-n)n=90n-n^2=n(43-n)-47(43-n)+43.47$
$=(n-47)(43-n)+2021$
Vì $n\leq 43$ nên $n-47< 0; 43-n\geq 0\Rightarrow (n-47)(43-n)\leq 0$
$\Rightarrow mn\leq 2021$. Giá trị này đạt tại $n=43, m=47$ thỏa mãn điều kiện đề.
Vậy GTLN của $mn$ là $2021$.
Đúng 0
Bình luận (0)
Cho m, n là các số nguyên dương thoả mãn 5m-n chia hết cho 5n-m. Chứng minh m chia hết cho n.
Ta thử lấy cặp số là m=1 và n=5 => 0:24 = 0 (thỏa mãn đề bài) Nhưng mà 1 làm gì chia hết cho 5
Đúng 0
Bình luận (0)
Cho m, n là các số nguyên dương thoả mãn 5m-n chia hết cho 5n-m. Chứng minh m chia hết cho n.
cho M,N là hai số nguyên thỏa mãn M+N=2 Chứng tỏ rằng M nhân N bé hơn hoặc bằng 1
vì M+N = 2 => M=1+k và N = 1-k
=> M.N = (1+k)(1-k) = 1-k+k-k2 = 1-k2 < 1 vì k2>0 với mọi k (đpcm)
Đúng 0
Bình luận (0)
cho hai số nguyên dương m,n thoả mãn \(\sqrt{3}>\frac{m}{n}\). Chứng minh rằng \(\sqrt{3}>\frac{m}{n}+\frac{1}{3mn}\)
Cho m,n,t là ba số nguyên tố lớn hơn 3 thoả mãn: m - n = n - t = a ( a ϵ N* ). Chứng minh rằng a chia hết cho 6.
Ai nhanh và đúng tick nhaaaa
cho 5 điểm A,B,C,M và N thoả mãn : 2 điểm A,B,C thẳng hàng , 3 điểm A,B,C ko thẳng hàng và 3 điểm A,B,N thẳng hàng
chứng tỏ 4 điểm A,B,C và N cùng thuộc 1 đường thẳng
có bao nhiêu thẳng phân biệt đi qua 2 điểm trong 5 điểm đã cho ? kể tên