Ta có: \(\overrightarrow{F}\cdot\Delta t=\Delta\overrightarrow{p}=\overrightarrow{p_{sau}}-\overrightarrow{p_{trc}}\)

\(\Rightarrow F\cdot\Delta t=6,54\cdot10^{-26}\cdot\left(-244-244\right)=-3,19152\cdot10^{-23}N\cdot s\)

Hai vật va chạm với nhau và sau khi va chạm chúng dính lại với nhau và chuyển động cùng vectơ vận tốc thì va chạm đó được coi là

A. va chạm đàn hồi.

B. va chạm mềm

C.va chạm cứng

D.va chạm lệch tâm

Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2  và   v ' 1 , v ' 2  là vận tốc của hai quả cầu trước và sau khi va chạm.

Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):

m 1 v ' 1  +  m 2 v ' 2  =  m 1 v 1  +  m 2 v 2

2. v ' 1  + 3. v ' 2  = 2.3 +3.1 = 9

Hay  v ' 1  + 1,5. v ' 2  = 4,5 ⇒  v ' 2  = 3 - 2 v ' 1 /3 (1)

Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:

m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2

2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2

Hay  v ' 1 2  + 1,5 v ' 2 2  = 10,5 ⇒  v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)

Giải hệ phương trình (1), (2), ta tìm được:  v ' 1 = 0,6 m/s;  v ' 2  = 2,6 m/s

(Chú ý: Loại bỏ cặp nghiệm  v ' 1  = 3 m/s,  v ' 2  = 1 m/s, vì không thỏa mãn điều kiện  v ' 2  >  v 2  = 1 m/s)

Giải thích: Đáp án D

Phương pháp :

-  Áp dụng định luật bảo toàn động lượng và định luật bảo toàn động năng

- Sử dung̣ hê ̣thức đôc̣ lâp̣ với thời gian của li đô ̣vàvâṇ tốc

Biên độ dao động ban đầu:

Cách giải:

Hai vật va chạm đàn hồi xuyên tâm nên áp dụng ĐL bảo toàn động lượng và động năng ta được:

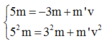
Giải hệ ta được v = 2cm/s

Áp dụng hệ thức độ lập: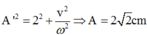

Vậy quãng đường đi được sau va chạm đến khi đổi chiều chuyển động là 

Theo bài ra ta có:  v₂ = v₁ = v = 600m/s

Chọn chiều dương là chiều chuyển động của phần tử khí trước khi chạm vào thành bình ta có  Δ p → = F → . Δ t

Chiếu theo chiều dương: 

F . Δ t = − m . v 2 − m v 1 = − 2 m v ⇒ F . Δ t = − 2.4 , 65.10 − 26 .600 = − 5 , 58.10 − 23 ( N . s )

+ Theo bài ra ta có:  

v 2 = v 1 = v = 600 m / s

+ Chọn chiều dương là chiều chuyển động của phần tử khí trước khi chạm vào thành bình ta có:  

Δ p → = F → . Δ t

+ Chiếu theo chiều dương:  

  F . Δ t = − m . v 2 − m v 1 = − 2 m v

⇒ F . Δ t = − 2.4 , 65.10 − 26 .600 = − 5 , 58.10 − 23 N . s

Chọn đáp án A

P/s: Bạn tự vẽ hình minh họa để dễ hiểu hơn 

Gọi \(\overrightarrow{p_1}\) là động lượng lúc trước và \(\overrightarrow{p_2}\) là động lượng lúc sau

Chọn (+) là chiều chuyển động ban đầu:

Từ mối liên hệ giữa động lượng và xung lượng của lực cho phần tử khí khi va chạm:

\(\overrightarrow{F}.\Delta t=\Delta\overrightarrow{p}\Leftrightarrow\overrightarrow{F}.\Delta t=\overrightarrow{p_2}-\overrightarrow{p_1}\)

chiếu (+) ta có: \(F.\Delta t=4.10^{-26}\left(-600-600\right)=-4,8.10^{-23}\left(N.s\right)\)

Lời giải

Hai vật va chạm đàn hồi trực diện. Chọn chiều dương là chiều chuyển động của viên bi 1. Ta có: 

v 2 ' = m 2 − m 1 v 2 + 2 m 1 v 1 m 1 + m 2 = 0 , 03 − 0 , 015 . ( − 18 ) + 2.0 , 015.22 , 5 0 , 03 + 0 , 015 = 9 c m / s

Với v 2   =   - 18   c m / s  vì viên bi 2 chuyển động ngược chiều so với viên bi 1

Đáp án: D

Bảo toàn động lượng ta có:

\(m_1v_1+m_2v_2=5m_1\)

\(\Leftrightarrow0,3v_1+0,1v_2=1,5\)

\(\Leftrightarrow3v_1+v_2=15\left(1\right)\)

Bảo toàn động năng lượng ta có:

\(\dfrac{1}{2}m_1v^2_1+\dfrac{1}{2}m_2v^2_2=\dfrac{25}{2}m_1\)

\(\Leftrightarrow3v^2_1+v_2^2=75\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình: 

\(\left\{{}\begin{matrix}3v_1+v_2=15\\3v_1^2+v^2_2=75\end{matrix}\right.\)

Giải hệ phương trình ta được:

\(\left\{{}\begin{matrix}v_1=2,5m/s\\v_2=7,5m/s\end{matrix}\right.\)