Hãy giải thích cách vẽ đồ thị của hàm: V = V0 (1 + αt) trong Hình 10.1a.

Những câu hỏi liên quan
( 1,75 điểm )
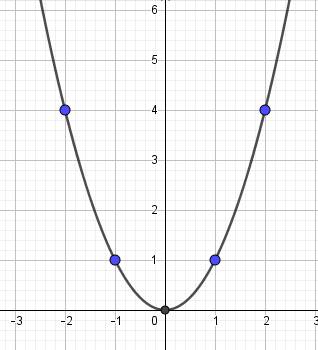
1) Xét tính đồng biến, nghịch biến của hàm số y = x2 và vẽ đồ thị (P) của hàm số đã cho trên mặt phẳng toạ độ Oxy.
2) Hỏi điểm M ( 3; 9 ) có thuộc đồ thị (P) hay không? Hãy giải thích.
1) Hàm số đồng biến khi x > 0 và nghịch biến khi x < 0
Bảng giá trị:

Đồ thị:
2) Thay tọa độ điểm M(3; 9) vào (P) ta được:
\(9=3^2\) (đúng)
Vậy điểm M(3; 9) thuộc đồ thị (P)
Đúng 2
Bình luận (0)
VẼ ĐỒ THỊ HÀM SỐ y=3−|x+1|
BÀI GIẢI (CÁCH XÁC ĐỊNH)+ GIẢI THÍCH CHI TIẾT GIÙM TỚ
Hình 9.10 biểu diễn đồ thị của ba hàm số. Hàm số thứ nhất là hàm vị trí của một chiếc ô tô, hàm số thứ hai biểu thị vận tốc và hàm số thứ ba biểu thị gia tốc của ô tô đó. Hãy xác định đồ thị của mỗi hàm số này và giải thích.
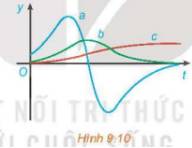
Hàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.
Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.
Đúng 0
Bình luận (0)
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
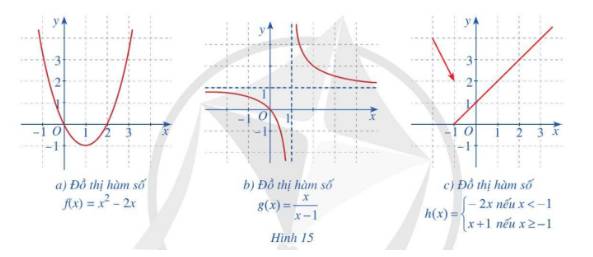
+) Hình 15a: Hàm số \(f\left( x \right) = {x^2}\;-2x\) có tập xác định \(D = \mathbb{R}.\)
Hàm số liên tục trên \(\mathbb{R}.\)
+) Hình 15b: Hàm số \(g\left( x \right) = \frac{x}{{x - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;1} \right)\)và \(\left( {1; + \infty } \right).\)
+) Hình 15c:
Với \(x\; \in \;\left( {-\infty ;-1} \right)\) có \(f\left( x \right) = -2x\) liên tục với mọi \(x\; \in \;\left( {-\infty ;-1} \right)\)
Với \(x\; \in \;\left( {-1; + \infty } \right)\) có \(f\left( x \right) = x + 1\) liên tục với mọi \(x\; \in \;\left( {-1; + \infty } \right)\)
Tại x = – 1 có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x} \right) = 2.\left( { - 1} \right) = - 2\\f\left( { - 1} \right) = - 1 + 1 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \ne f\left( { - 1} \right)\end{array}\)
Do đó hàm số không liên tục tại x = – 1.
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;-1} \right)\)và \(\left( {-1; + \infty } \right).\)
Đúng 0
Bình luận (0)
Biết đồ thị hàm số
y
2
x
-
2
x
+
1
là hình vẽ sau: Đồ thị hàm số
y
2
x
-
2
x
+...
Đọc tiếp
Biết đồ thị hàm số y = 2 x - 2 x + 1 là hình vẽ sau:
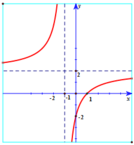
Đồ thị hàm số y = 2 x - 2 x + 1 là hình vẽ nào trong 4 hình vẽ sau:
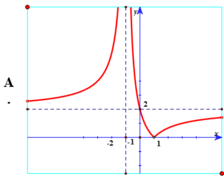
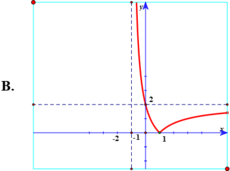
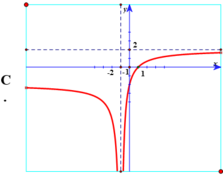
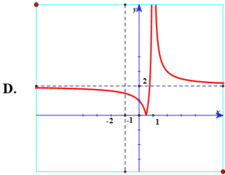
Chọn A.
Ta có:
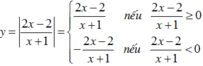
Đồ thị hàm số y = 2 x - 2 x + 1 có được bằng cách:
+ Giữ nguyên phần đồ thị hàm số y = 2 x - 2 x + 1 nằm phía trên trục hoành.
+ Lấy đối xứng phần đồ thị hàm số y = 2 x - 2 x + 1 nằm phía dưới trục hoành qua trục hoành.
Đúng 0
Bình luận (0)
Cho y= f(x)+2x và y= g(x)= -x - 3
ko vẽ hình, hãy tìm tọa độ giao điểm của đồ thị của 2 hàm số trên
( nêu cách giải cụ thể luôn nha )
Cho hàm số y=x
Hãy vẽ đồ thị của hàm số trên bằng cách chỉ ra 2 điểm khác nhau thuộc đồ thị.
đang cần gấp
hình đây nhé:
Đồ thị hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây? A.
y
-
x
4
+
2
x
2
+
2
B.
y
x
4
+
2
x
2
+
2
C.
y
x
4
-
4
x
2...
Đọc tiếp
Đồ thị hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
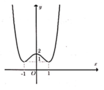
A. y = - x 4 + 2 x 2 + 2
B. y = x 4 + 2 x 2 + 2
C. y = x 4 - 4 x 2 + 2
D. y = - x 4 - 2 x 2 + 3
Dựa vào đồ thị thấy phía bên phải hướng lên nên hệ số của x 4 phải dương nên loại A.
Để ý thấy khi x = 0 thì y = 2 nên ta loại D.
Hàm số đạt cực trị tại x = 0 và x = ± 1 nên chỉ có B phù hợp vì
y ' = 4 x 3 - 4 x = 4 x x 2 - 1 y ' = 0 ⇔ x = 0 x = ± 1
Đáp án B
Đúng 0
Bình luận (0)
Trong hình vẽ bên đồ thị (1) là của hàm số y logax và đồ thị (2) là của hàm số y logbx. Khẳng định nào sau đây là đúng. A. a b 1 B. b a 1 C. 1 a b 0 D. 1 b a 0
Đọc tiếp
Trong hình vẽ bên đồ thị (1) là của hàm số y = logax và đồ thị (2) là của hàm số y = logbx. Khẳng định nào sau đây là đúng.
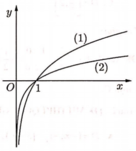
A. a > b > 1
B. b > a > 1
C. 1 > a > b > 0
D. 1 > b > a > 0
Chọn B.
Dựa vào đồ thị ta thấy 2 hàm số đã cho phải là 2 hàm đồng biến như vậy a; b > 1
Mặt khác chọn x = 2 ta có:
![]()
Do đó b > a > 1.
Đúng 0
Bình luận (0)















