Bài  Bài 6 ạ Giải hộ mình nhen
Bài 6 ạ Giải hộ mình nhen

Những câu hỏi liên quan
 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Đúng 2
Bình luận (0)
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm
Đúng 2
Bình luận (0)
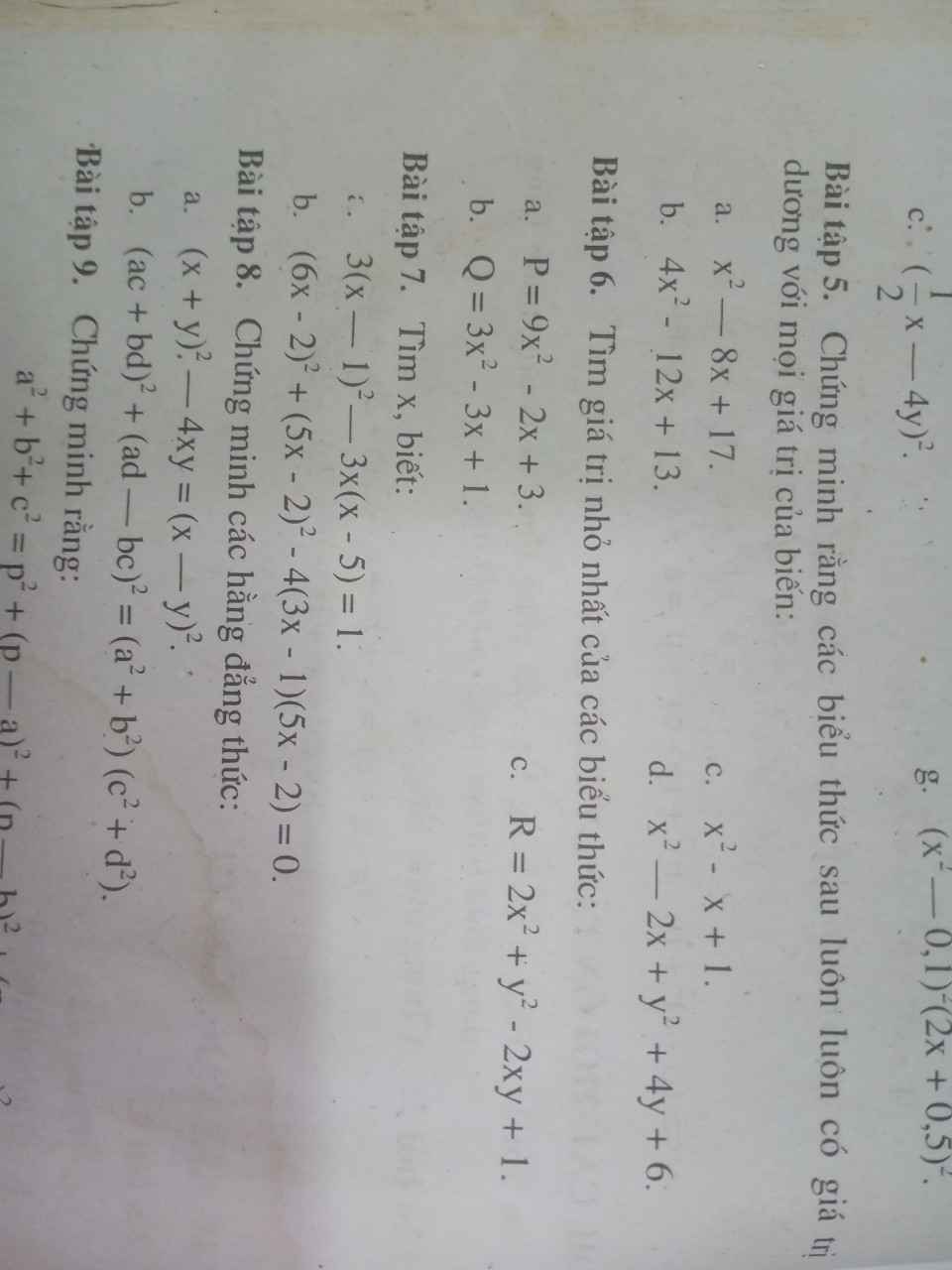
GIẢI HỘ MÌNH BÀI 5 VỚI 6 VỚI Ạ!
Bài 5:
a: Ta có: x2−8x+17x2−8x+17
=x2−8x+16+1=x2−8x+16+1
=(x−4)2+1>0∀x=(x−4)2+1>0∀x
b: Ta có: 4x2−12x+134x2−12x+13
=4x2−12x+9+4=4x2−12x+9+4
=(2x−3)2+4>0∀x=(2x−3)2+4>0∀x
c: Ta có: x2−x+1x2−x+1
=(x−12)2+34>0∀x
Đúng 0
Bình luận (0)
Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
Đúng 0
Bình luận (0)
Bài 5:
a. $x^2-8x+17=(x^2-8x+16)+1=(x-4)^2+1$
$\geq 0+1>0$ với mọi $x\in\mathbb{R}$ (đpcm)
b. $4x^2-12x+13=(4x^2-12x+9)+4$
$=(2x-3)^2+4\geq 0+4>0$ với mọi $x\in\mathbb{R}$ (đpcm)
c. $x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $x\in\mathbb{R}$ (đpcm)
d.
$x^2-2x+y^2+4y+6=(x^2-2x+1)+(y^2+4y+4)+1$
$\geq (x-1)^2+(y+2)^2+1$
$\geq 0+0+1>0$ với mọi $x,y\in\mathbb{R}$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

Giải hộ mình bài ,8 ( bài 8 vẽ hình luôn hộ mình ) Mình cảm ơn ạ
Giải hộ mình bài 4,5,8 ( bài 8 vẽ hình luôn hộ mình )
Mình cảm ơn ạ 
Giải chi tiết giúp mình bài này hộ với ạ
(√27 - 3√2 +2√6) : 3√3
đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)
Đúng 2
Bình luận (1)
và bài này luôn quên không viết
√(√3 +1)^2 + √(1- √3)^2
Đúng 0
Bình luận (0)
\(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(1-\sqrt{3}\right)^2}=\sqrt{3}+1\sqrt{3}-1=2\sqrt{3}\)
Đúng 1
Bình luận (2)
Giải hộ mình bài này với nhen
Mẹ sinh Long năm mẹ 32 tuổi. Hỏi khi tổng số mẹ và Long là 48 thì Long bao nhiêu tuổi?
goi số tuổi của long khi tổng tuổi của mẹ và long là 48 là x
=> ta có ct
=> x + (32+x ) =48
=> 2x+32=48
=> 2x= 48-32=16
x=16/2 = 8
vậy long 8 tuổi thì tổng số tuổi của mẹ và long là 48
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

giải hộ bài 5 bài 6 vs ạ
6:
a:
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
=>AEDF là hình chữ nhật
Xet ΔDEB vuông tạiE và ΔCFD vuông tại F có
DE=CF
EB=FD
=>ΔDEB=ΔCFD
b: Xet ΔAED vuông tại E và ΔDFA vuông tại F có
AE=DF
ED=FA
=>ΔAED=ΔDFA
Đúng 0
Bình luận (0)
Ai giúp mình bài này với ạ ! Mình cần gấp ạ , cảm ơn trc nhen ☺️✌️

giải cho mình bài 27.11, 28.18 SBT lớp 7 với ạ ghi hộ mình tóm tắt bài toán luôn ạ
bài 27,11:TÓM TẮT :
I=0,25A
U=5,8V; U1=2,8V
TÍNH I1,I2,U2?
a) vì Đ1 nối tiếp với Đ2 nên ta có : I=I1=I2
=> cường độ dòng điện chạy qua đèn 1 là : I1=I=0,25A
Cường đọ dòng điện chạy qua đèn 2 là : I2=I=0,25A
b) vì Đ1 nối tiếp Đ2 nên ta có : U=U1+U2
=> Hiệu điện thế giữa 2 đầu đèn 2 là : U2=U=U1
=> U2=5,8V - 2,8 V
=> U2= 3V
c) cả 2 đèn đều sáng hơn
bài 28.18:TÓM TẮT:
U1=2,8V
I=0,45A;I1=0,22A
TÍNH U2,I2?
a) vì Đ1 song song Đ 2 nên U=U1=U2
=>ta có :U=U1=2,8V
=> hiệu điện thế giữa 2 đầu đèn 2 là :
U=U2=2,8V
b) vì Đ1 song song Đ2 nên ta có : I=I1+I2
=> cường độ dòng điện chạy qua Đ2 là :
=> I2=I-I1
=> I2= 0,45A-0,22A
=> I2=0,23 A
CHÚC BẠN HỌC TỐT !!!
Giải hộ mình bài bày với ạ, mình cảm ơn nhiều ạ ^^ <3 
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m+2\right)x-2m\)
\(\Leftrightarrow x^2-\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2-8m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\)
mà \(\left(m-2\right)^2\ge0\)
nên \(m-2\ne0\)
hay \(m\ne2\)
Vậy: Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(m\ne2\)
Đúng 1
Bình luận (0)






















