Đường cao ứng vs cạnh huyền của 1 tam giác vuông cân có độ dài bằng 2cm. Giải tam giác vuông đó.

Những câu hỏi liên quan
Cho 1 tam giác vuông có cạnh huyền bằng 5 cm. 2 cạnh góc vuông của tam giác vuông đó hơn kém nhau 20mm. Tính độ dài đường cao ứng với cạnh huyền của tam giác vuông đó.
Giải bài toán bằng cách lập phương trình
Một tam giác vuông có đường cao ứng với cạnh huyền dài 24cm và chia cạnh huyền thành hai đoạn thẳng hơn kém nhau 14cm.Tính độ dài cạnh huyền và diện tích của tam giác vuông đó
Gọi độ dài đoạn thẳng ngắn hơn được chia trên cạnh huyền là x (cm) với x>0
\(\Rightarrow\) Độ dài đoạn còn lại là \(x+14\)
Áp dụng hệ thức lượng trong tam giác vuông:
\(24^2=x\left(x+14\right)\)
\(\Leftrightarrow x^2+14x-576=0\Rightarrow\left[{}\begin{matrix}x=18\\x=-32\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\) Độ dài cạnh huyền là: \(18+\left(18+14\right)=50\left(cm\right)\)
Diện tích tam giác: \(S=\dfrac{1}{2}.24.50=600\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho 1 tam giác vuông có cạnh huyền 5cm. 2 cạnh góc vuông tam giác vuông đó hơn kém nhau 20mm. Tính độ dài đường cao ứng với cạnh huyền tam giác vuông đó.
Gọi độ dài cạnh góc vuông 1 là x
=>Độ dài cạnh góc vuông 2 là x+2
Theo đề, ta có: x^2+x^2+4x+4=5^2=25
=>2x^2+4x-21=0
=>x=(-2+căn 46)/2
=>Độ dài cạnh góc vuông 2 là (2+căn 46)/2
Độ dài đường cao là:
\(\dfrac{\left(-2+\sqrt{46}\right)\left(2+\sqrt{46}\right)}{2}:5=\dfrac{46-4}{2}:5=\dfrac{42}{10}=4,2\)
Đúng 0
Bình luận (0)
bài 1: Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4,kẻ đường cao tương ứng vs cạnh huyền .Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền
bài 2: Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2.Hãy tính các cạnh góc vuông của tam giác này
AI GIÚP VS HELP ME CẦN GẤP
Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
Đúng 0
Bình luận (0)
Bài 2:
Ta có: △ABC vuông tại A và có đg cao AH
AB2 = BH.BC ( hệ thức lượng )
⇒ x2 = 1 . 3
⇒ x = \(\sqrt{1.3}=\sqrt{3}cm\)
AC2 = CH.BC
⇒ y2 = 2 . 3
⇒ y = \(\sqrt{6}\) cm
Đúng 0
Bình luận (0)
Trong một tam giác vuông đường cao ứng với cạnh huyền chia tam giác thành hai phần có diện tích bằng 54cm2 và 96cm2. hãy tính độ dài đường cao và cạnh huyền của tam giác đó.
có S AHB = AH.HB/2 = 54 (gt) => AH.HB = 108
S AHC = AH.HC/2 = 96 (gt) => AH.HC = 192
=> AH^2.HB.HC = 108.192 = 20736 (1)
tg ABC có ^A = 90 (gt) ; AH _|_ BC => AH^2 = HB.HC (đl)
=> AH^4 = AH^2.HB.HC và (1)
=> AH^4 = 20736
=> AH = 12 do AH > 0
có AH.HB = 108 => HB = 9
AH.HC = 192 => HC = 16
=> HB + HC = 9 + 16 = 25
Một tam giác vuông có độ dài hai cạnh góc vuông là
log
2
x
và
log
2
(
64
x
)
. Biết rằng đường cao tương ứng với cạnh huyền của tam giác đó có độ dài bằng 2. Tìm x. A. x 8 B. x 64 C. x 2 D. x 6
Đọc tiếp
Một tam giác vuông có độ dài hai cạnh góc vuông là log 2 x và log 2 ( 64 x ) . Biết rằng đường cao tương ứng với cạnh huyền của tam giác đó có độ dài bằng 2. Tìm x.
A. x = 8
B. x = 64
C. x = 2
D. x = 6
Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.
Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
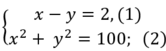
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100 ⇔ 2 y 2 + 4 y − 96 = 0 hay y 2 + 2 y − 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( loại)
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.
Đúng 0
Bình luận (0)
Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.
Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
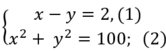
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100
⇔ 2 y 2 + 4 y – 96 = 0 h a y y 2 + 2 y – 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( l o ạ i )
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.
Đúng 0
Bình luận (0)
cạnh bé nhất của 1 tam giác vuông có độ dài =6cm,cạnh huyền có độ dài lớn hơn cạnh góc vuông còn lại 2cm. tính độ dai cạnh huyền của tam giác vuông đó
















