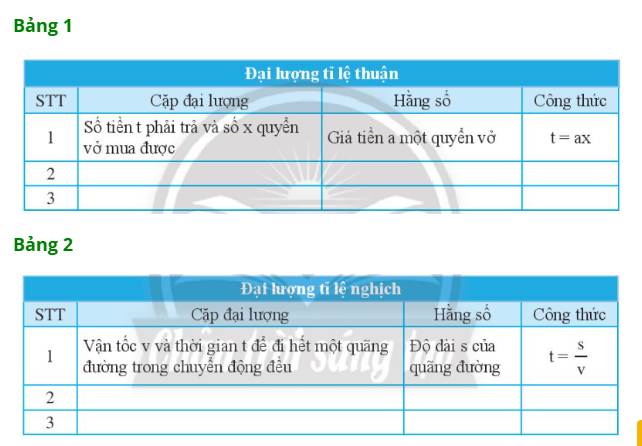
 Hãy tìm các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế rồi ghi vào hai bảng.
Hãy tìm các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế rồi ghi vào hai bảng.

Những câu hỏi liên quan
Cho 3 đại lượng x,y,z.Hãy tìm hiểu sự tương quan giữa các đại lượng x và y, biết rằng:
a)x và y là hai đại lượng tỉ lệ nghịch; y và z là hai đại lượng tỉ lệ nghịch
b)x và y là hai đại lượng tỉ lệ nghịch; và z là hai đại lượng tỉ lệ thuận
c) x và y là hai đại lượng tỉ lệ thuận;y và z là hai đại lượng tỉ lệ nghịch.
Mục tiêuVận dụng kiến thức về đại lượng tỉ lệ để nhận biết các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế. Qua đó ôn tập và củng cố các tính chất cơ bản của các đại lượng tỉ lệ.Chuẩn bị- Chia lớp theo nhóm học tập từ 8 đến 10 học sinh.- Mỗi nhóm chuẩn bị một tờ bìa có ghi hai bảng thống kê theo mẫu.Tiến hành hoạt động- Nhóm trưởng phân công một số bạn trong nhóm tìm các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế để ghi vào hai bảng.- Nhóm trưởng cùng các bạn còn lại kiểm tra và...
Đọc tiếp
Mục tiêu
Vận dụng kiến thức về đại lượng tỉ lệ để nhận biết các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế. Qua đó ôn tập và củng cố các tính chất cơ bản của các đại lượng tỉ lệ.
Chuẩn bị
- Chia lớp theo nhóm học tập từ 8 đến 10 học sinh.
- Mỗi nhóm chuẩn bị một tờ bìa có ghi hai bảng thống kê theo mẫu.
Tiến hành hoạt động
- Nhóm trưởng phân công một số bạn trong nhóm tìm các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế để ghi vào hai bảng.
- Nhóm trưởng cùng các bạn còn lại kiểm tra và ghi thông tin vào các cột theo yêu cầu trong bảng.
- Các nhóm báo cáo trước lớp.
- Giáo viên cho nhận xét và đánh giá theo ba tiêu chí: đúng, đầy đủ và phong phú.
Chú ý:
- Có thể cho các nhóm bốc thăm để mỗi nhóm chỉ cần tìm một loại đại lượng tỉ lệ thuận hoặc tỉ lệ nghịch.
- Học sinh có thể truy cập vào internet để tìm kiếm các đại lượng tỉ lệ và làm trang trình chiếu minh họa.
Cho biết hai đại lượng x và y tỉ lệ nghịch theo hệ số tỉ lệ là 5, hai đại lương y và z tỉ lệ nghịch với nhau theo hệ số tỉ lệ 4. Hãy chứng tỏ x và z tỉ lệ thuận. Tìm hệ số tỉ lệ.
xy=5
yz=4
nên x=4/z
xy=5
nên 4x/z=5
=>4x=5z
=>x=5/4z
Vậy: x và z tỉ lệ thuận
Đúng 0
Bình luận (1)
6.28
cho 3 đại lượng x ,y z .Tìm mối quan hệ giữa hai đại lượng x và z , biết rằng :
a ) x và y tỉ lệ thuận , y và z tỉ lệ thuận
b ) x và y tỉ lệ thuận , y và z tỉ lệ nghịch
c ) x và y tỉ lệ nghịch , y và z tỉ lệ nghịch
a) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên \(y=a.x\) nên \(x=\dfrac{y}{a}\)
y tỉ lệ thuận với z theo hệ số tỉ lệ b nên \(y=b.z\)
Do đó, \(x=\dfrac{y}{a}=\dfrac{b.z}{a}=\dfrac{b}{a}.z\left(\dfrac{b}{a}\text{là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
b) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x=\dfrac{y}{a}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên \(y=\dfrac{b}{z}\)
Do đó: \(x=\dfrac{y}{a}=\dfrac{\dfrac{b}{z}}{a}=\dfrac{b}{z}:a=\dfrac{b}{z}.\dfrac{1}{a}=\dfrac{\dfrac{b}{a}}{z}\left(\dfrac{b}{a}\text{là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ nghịch với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
c) Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(y=\dfrac{a}{x}\) nên \(x=\dfrac{a}{y}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên \(y=\dfrac{b}{z}\)
Do đó: \(x=\dfrac{a}{y}=\dfrac{a}{\dfrac{b}{z}}=a:\dfrac{b}{z}=a.\dfrac{z}{b}=\dfrac{a}{b}.z\left(\dfrac{a}{b}\text{ là hằng số vì a,b là các hằng số}\right)\)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)
Đúng 2
Bình luận (1)
Cho biết hai đại lượng x và y tỉ lệ nghịch theo hệ số tỉ lệ là 5, hai đại lượng y và z tỉ lệ nghịch với nhau theo hệ số tỉ lệ 3. Hỏi x và z tỉ lệ thuận hay tỉ lệ nghịch. Tìm hệ số tỉ lệ
`@` `\text {dnammv}`
Ta có:
`x` và `y` tỉ lệ nghịch với nhau theo hệ số tỉ lệ `5`
`-> x=5/y` `(1)`
`y` và `z` tỉ lệ nghịch với nhau theo hệ số tỉ lệ `3`
`-> y=3/z` `(2)`
Từ `(1)` và `(2)`
`-> x=5/(3/z)`
`x=5*z/3 = 5/3*z`
Vậy, `x` tỉ lệ thuận với `z` theo hệ số tỉ lệ `5/3.`
Đúng 2
Bình luận (0)
x và y tỉ lệ nghịch theo hệ số tỉ lệ 5 nên y=5/x
y và z tỉ lệ nghịch theo hệ số tỉ lệ 3 nên y=3/z
=>5/x=3/z
=>3x=5z
=>x=5/3z
=>x và z tỉ lệ thuận theo hệ số tỉ lệ 5/3
Đúng 0
Bình luận (0)
Đại lượng x tỉ lệ nghịch với đại lượng ý theo hệ số tỉ lệ 0.2 . Đại lượng ý tỉ lệ nghịch với đại lượng z theo hệ số tỉ lệ là 3. Hỏi đại lượng x và đại lượng z là hai đại lượng tỉ lệ thuận hay tỉ lệ nghịch. Tìm hệ số tỉ lệ
mình chưa học bạn à . Xin lỗi bạn nhé vì ko giải được cho bạn
Đúng 0
Bình luận (0)
Cho ba đại lượng x,y,z. Tìm mối quan hệ giữa hai đại lượng x và z, biết rằng:
a) x và y tỉ lệ thuận, y và z tỉ lệ thuận
b) x và y tỉ lệ thuận, y và z tỉ lệ nghịch
c) x và y tỉ lệ nghịch, y và z tỉ lệ nghịch
a) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ thuận với z theo hệ số tỉ lệ b nên y = b.z
Do đó, \(x = \dfrac{y}{a} = \dfrac{{b.z}}{a} = \dfrac{b}{a}.z\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
b) Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x nên \(x = \dfrac{y}{a}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{y}{a} = \dfrac{{\dfrac{b}{z}}}{a} = \dfrac{b}{z}:a = \dfrac{b}{z}.\dfrac{1}{a} = \dfrac{{\dfrac{b}{a}}}{z}\)( \(\dfrac{b}{a}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ nghịch với z và hệ số tỉ lệ là \(\dfrac{b}{a}\)
c) Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên y = \(\dfrac{a}{x}\) nên x = \(\dfrac{a}{y}\)
y tỉ lệ nghịch với z theo hệ số tỉ lệ b nên y = \(\dfrac{b}{z}\)
Do đó, \(x = \dfrac{a}{y} = \dfrac{a}{{\dfrac{b}{z}}} = a:\dfrac{b}{z} = a.\dfrac{z}{b} = \dfrac{a}{b}.z\)( \(\dfrac{a}{b}\) là hằng số vì a,b là các hằng số)
Vậy x tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)
Đúng 0
Bình luận (0)
Câu 1. Cho ba đại lượng x, y, z. Hãy tìm mối tương quan giữa hai đại lượng x và z, biết:
a) x tỉ lệ thuận với y theo hệ số tỉ lệ 2, y tỉ lệ nghịch với z theo hệ số tỉ lệ -3.
b) x tỉ lệ nghịch với y theo hệ số tỉ lệ 5, y tỉ lệ nghịch với z theo hệ số tỉ lệ 3.
a: x=2y
nên y=2/x
yz=-3
\(\Leftrightarrow z\cdot\dfrac{2}{x}=-3\)
\(\Leftrightarrow2z=-3x\)
Đúng 0
Bình luận (0)
Các giá trị của hai đại lượng x và y được cho bởi bảng sau đây:x0,511,522,5y2,557,51012,5Hỏi hai đại lượng x và y có quan hệ tỉ lệ thuận hay tỉ lệ nghịch không? Viết công thức liên hệ giữa x và y.
Đọc tiếp
Các giá trị của hai đại lượng x và y được cho bởi bảng sau đây:
x | 0,5 | 1 | 1,5 | 2 | 2,5 |
y | 2,5 | 5 | 7,5 | 10 | 12,5 |
Hỏi hai đại lượng x và y có quan hệ tỉ lệ thuận hay tỉ lệ nghịch không? Viết công thức liên hệ giữa x và y.
Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)
Đúng 1
Bình luận (0)
Cho 3 đại lượng tỉ lệ nghịch là x, y, z. Hãy cho biết mối liên hệ giữa hai đại lượng x và y biết :
a) x và y tỉ lệ nghịch; y và z tỉ lệ nghịch
b) x và y tỉ lệ nghịch; y và z tỉ lệ thuận


















