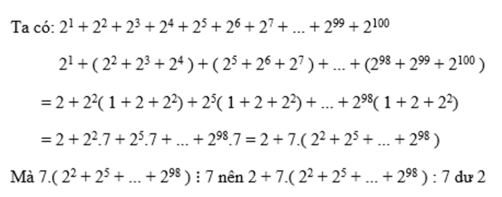Tìm số dư của 21 + 22 +23 +.....+22016 +22017 khi chia cho 217

Những câu hỏi liên quan
Tìm dư của phép chia số A = 22021 + 22022 chia cho B = 1 + 2 + 22 + 23 +....+22016 + 22017
A=21+22+23+...+22016
chứng tỏ A chia hết cho 7
\(A=2^1+2^2+2^3+...+2^{2016}\)
\(\Rightarrow A=2\left(1+2^1+2^2\right)+2^4\left(1+2^1+2^2\right)...+2^{2014}\left(1+2^1+2^2\right)\)
\(\Rightarrow A=2.7+2^4.7...+2^{2014}.7\)
\(\Rightarrow A=7\left(2+2^4...+2^{2014}\right)⋮7\)
\(\Rightarrow dpcm\)
Đúng 3
Bình luận (0)
1, Cho số a = 82017 . 253024. Hỏi số a có bao nhiêu chữ số?
2, Tìm dư của phép chia số a = 22020 cho số b = 1+2+22+23+...+22017
1, Cho số a = 82017 . 253024. Hỏi số a có bao nhiêu chữ số?
2, Tìm dư của phép chia số a = 22020 cho số b = 1+2+22+23+...+22017
21+ 22 + 23+... +22017
`@` Đặt `A=2^1+2^2+2^3+...+2^2017`
`=>2A=2(2^1+2^2+2^3+...+2^2017)`
`=>2A=2^2+2^3+...+2^2018`
`=>2A-A=(2^2+2^3+...+2^2018)-(2^1+2^2+...+2^2017)`
`=>A=2^2018-2`
Đúng 0
Bình luận (0)
Số dư của A = 20 + 21 + 22 + 23 + .......... + 2100 khi chia cho 100 là: ................
Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
Đúng 0
Bình luận (0)
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
A=20+21+22+23+24+.........+22015+22016
Tìm số dư khi chia A cho 7.![]()
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016
=7(1+2^3+...+2^2013)+2^2016
Vì 2^2016 chia 7 dư 1
nên A chia 7 dư 1
Đúng 0
Bình luận (0)
S = 2+2.22+3.23 +... +2016.22016
1) Chứng tỏ S+2013 chia hết cho 22017+1
2) Tìm số dư khi chia S cho 8
\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)
\(2S=2^2+2.2^3+3.2^4+...+2016.2^{2017}\)
\(2S-S=S=\text{}\text{}\text{}\text{}2^2+2.2^3+3.2^4+...+2016.2^{2017}-2-2.2^2-3.2^3-...-2016.2^{2016}\)
\(S=2\left(0-1\right)+2^2\left(1-2\right)+2^3\left(2-3\right)+...+2^{2016}\left(2015-2016\right)+2^{2017}.2016\)
\(S=-\left(2+2^2+2^3+...+2^{2016}\right)+2^{2017}.2016\)
\(\)Đặt \(A=2+2^2+2^3+...+2^{2016}\)
\(2A=2^2+2^3+2^4+...+2^{2017}\)
\(2A-A=A=2^2+2^3+2^4+...+2^{2017}-2-2^2-2^3-...-2^{2016}\)
\(A=2^{2017}-2\)
Thay vào S ta được:
\(S=-2^{2017}+2+2^{2017}.2016\)
\(S=2^{2017}.2015+2\)
Ta có \(S+2013=2^{2017}.2015+2+2013\)
\(S+2013=2^{2017}.2015+2015\)
\(S+2013=2015\left(2^{2017}+1\right)\)
Suy ra \(S+2013⋮2^{2017}+1\)
Vậy \(S+2013⋮2^{2017}+1\) (đpcm)
Đúng 3
Bình luận (0)
\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)
\(S=2+2^3+3.2^3+...+2016.2^{2016}\)
\(S=2+2^3\left(1+3+...+2016.2^{2013}\right)\)
\(S=2+8.\left(1+3+...+2016.2^{2013}\right)\)
Suy ra \(S\) chia \(8\) dư \(2\)
Vậy \(S\) chia \(8\) dư \(2\)
Gửi bạn nha, bài này làm hơi dài ^^
Đúng 0
Bình luận (0)