cho hai điểm A,B treen đường tròn bán kính R sao cho AB không phải là đường kính . Gọi M là trung điểm của AB . Lấy điểm N bất kì trên tia OM ( n khác O , M khác O ) . Chứng minh AN = BN

Những câu hỏi liên quan
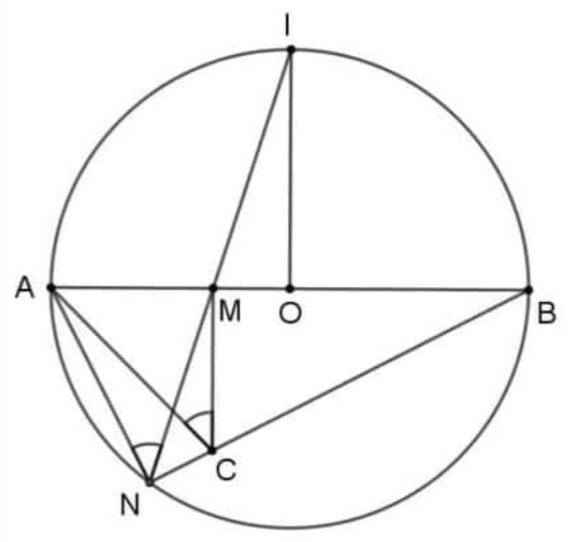
Cho đường tròn (O;R)), đường kính AB. Gọi I là điểm chính giữa cung AB. Lẫy điểm M bất kì trên đoạn thẳng OA (M khác OO và A)A). Tia IM cắt đường tròn tại điểm thứ hai N. Đường thẳng qua M, vuông góc với AB cắt đoạn thẳng BN tại C. a) Chứng minh bốn điểm A, M,C,N cùng thuộc một đường tròn. b) Tính số đo góc AMN và chứng minh AMMC. c) Khi M thay đổi trên đoạn OA, chứng minh MNR.
Đọc tiếp
Cho đường tròn (O;R)), đường kính AB. Gọi I là điểm chính giữa cung AB. Lẫy điểm M bất kì trên đoạn thẳng OA (M khác OO và A)A). Tia IM cắt đường tròn tại điểm thứ hai N. Đường thẳng qua M, vuông góc với AB cắt đoạn thẳng BN tại C. a) Chứng minh bốn điểm A, M,C,N cùng thuộc một đường tròn. b) Tính số đo góc AMN và chứng minh AM=MC. c) Khi M thay đổi trên đoạn OA, chứng minh MN<R.
a) dễ thấy \(\widehat{AMC}\) \(=\) \(90^o\) xét (O) có đường kính \(AB\) \(\Rightarrow\) \(\widehat{ANB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\) \(\widehat{ANB}\) \(=90^o\) hay \(\widehat{ANC}\) \(=90^o\) . tứ giác \(ANCM\) có :
\(\widehat{AMC}\) \(+\) \(\widehat{ANC}\) \(=90^o+90^o=180^o\) \(\Rightarrow\) tứ giác \(ANCM\) nội tiếp 4 điểm \(A,N,C,M\) cùng \(\in\) 1 đường tròn
b) vì \(AB\) là đường kính của (O) \(\Rightarrow\) \(\stackrel\frown{AB}\) \(=180^o\)
mà \(I\) là điểm chính giữa của \(\stackrel\frown{AB}\)
\(\Rightarrow\) \(A=\dfrac{\stackrel\frown{AB}}{2}\) \(=\dfrac{180^o}{2}=90^o\)
có \(\widehat{ANI}\) là góc nội tiếp chắn \(\stackrel\frown{IA}\)
\(\Rightarrow\) \(\widehat{ANI}\) \(=\dfrac{1}{2}\) ; \(A=\dfrac{1}{2}.90^o\) \(=45^o\) hay \(\widehat{ANM}\) \(=45^o\) . mặt khác , tứ giác \(ANCM\) nội tiếp \(\Rightarrow\) \(\widehat{ANM}\) \(=\) \(\widehat{ACM}\) mà \(\widehat{ANM}\) \(=45^o\) \(\Leftrightarrow\) \(\widehat{ACM}\) \(=45^o\) lại có \(\Delta ACM\) cuông tại \(M\) \(\Rightarrow\) \(\Delta ACM\) vuông cân tại \(M\)
\(\Rightarrow\) \(AM=CM\)
c) kẻ đường kính \(ID\) của (O) :
có : \(MN=IN-IM\) mà \(IN\) là dây của (O) nên hiển nhiên \(IN\le ID\) nhưng do \(IN\) không qua (O) nên \(IN< ID\) (1) , dễ dàng chứng minh \(IO\perp AB\) tại \(O\)
do vậy : \(\Delta IOM\) vuông tại (O) \(\Rightarrow\) \(IM>IO\) ( không xảy ra dấu " = " vì \(M\) không trùng với \(O\) )
\(\Leftrightarrow\) \(-IM< -IO\) (2)
từ (1) và (2)
\(\Rightarrow\) \(IN-IM< ID-IO\) \(\Leftrightarrow\) \(MN< OD\) \(=R\)
vậy ta có \(đpcm\)
Đúng 2
Bình luận (1)
Cho đường tròn (O), bán kính R. Từ 1 điểm M nằm ngoài đường tròn vẽ 2 tiếp tuyến MA và MA của đường tròn ( A,B là 2 tiếp điểm ). Gọi H là giao điểm của AB và MO.a, Chứng Minh 4 điểm M,A,O,B cùng thuộc 1 đường trònb, Kẻ đường kính BD. Chứng minh rằng AD//MO và OH*OMR2c, Trên OA lấy điểm N sao cho AN2ON. Gọi F là trung điểm của AN. Đường trung trực của BN cắt OM tại E. Chứng minh EF//MA và tính tỉ số frac{OE}{OM}
Đọc tiếp
Cho đường tròn (O), bán kính R. Từ 1 điểm M nằm ngoài đường tròn vẽ 2 tiếp tuyến MA và MA của đường tròn ( A,B là 2 tiếp điểm ). Gọi H là giao điểm của AB và MO.
a, Chứng Minh 4 điểm M,A,O,B cùng thuộc 1 đường tròn
b, Kẻ đường kính BD. Chứng minh rằng AD//MO và OH*OM=R2
c, Trên OA lấy điểm N sao cho AN=2ON. Gọi F là trung điểm của AN. Đường trung trực của BN cắt OM tại E. Chứng minh EF//MA và tính tỉ số \(\frac{OE}{OM}\)
Cho nửa đường tròn(O;R), đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Bx với (O). M là điểm bất kì trên Bx(M khác B), AM cắt nửa đường tròn (O) tại N (N khác A). Kẻ OE vuông góc với AN tại E.a) Chứng minh các điểm E, O, B, Mcùng thuộc đường trònb) Tiếp tuyến của nửa đường tròn (O) tại N cắt tia OE tại K và cắt MB tại D. Chứng minh KA là tiếp tuyến của nửa đường tròn (O).c) Chứng minh KA.DB không đổi khi M di động trên tia Bxd) Gọi H là giao điểm của AB và DK, kẻ OF...
Đọc tiếp
Cho nửa đường tròn(O;R), đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Bx với (O). M là điểm bất kì trên Bx(M khác B), AM cắt nửa đường tròn (O) tại N (N khác A). Kẻ OE vuông góc với AN tại E.
a) Chứng minh các điểm E, O, B, Mcùng thuộc đường tròn
b) Tiếp tuyến của nửa đường tròn (O) tại N cắt tia OE tại K và cắt MB tại D. Chứng minh KA là tiếp tuyến của nửa đường tròn (O).
c) Chứng minh KA.DB không đổi khi M di động trên tia Bx
d) Gọi H là giao điểm của AB và DK, kẻ OF vuông góc với AB(F thuộc DK). Chứng minh: BD/DF+DF/HF=1
a: Xét tứ giác OBME có
\(\widehat{OBM}+\widehat{OEM}=180^0\)
Do đó: OBME là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và đường thẳng (Δ) không có điểm chung với đường tròn (O) , H là hình chiếu vuông góc của O trên (Δ) . Từ điểm M bất kỳ trên (Δ) (M≠≠H) , vẽ hai tiếp tuyến MA, MB tới đường tròn (O) (A,B là hai tiếp điểm ) . Gọi K, I thứa tự là giao điểm của AB với OM và OH .1. chứng minh AB2AK và 5 điểm M;A;O;B;H cùng thuộc đường tròn .2. Chứng minh OI.OHOK.OMR223. Trên đoạn OA lấy điểm N sao cho AN2ON. Đường trung trực của BN cắt OM ở E . Tính tỷ số OEOM
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng (Δ) không có điểm chung với đường tròn (O) , H là hình chiếu vuông góc của O trên (Δ) . Từ điểm M bất kỳ trên (Δ) (M≠≠H) , vẽ hai tiếp tuyến MA, MB tới đường tròn (O) (A,B là hai tiếp điểm ) . Gọi K, I thứa tự là giao điểm của AB với OM và OH .
1. chứng minh AB=2AK và 5 điểm M;A;O;B;H cùng thuộc đường tròn .
2. Chứng minh OI.OH=OK.OM=R22
3. Trên đoạn OA lấy điểm N sao cho AN=2ON. Đường trung trực của BN cắt OM ở E . Tính tỷ số OEOM
Cho đường tròn tâm O bán kính r dây AB=R căn 3 và K là điểm chính giữa cung lớn AB.Gọi M là điểm tùy ý trên cung nhỏ BK(M khác B;K).Trên tia AM lấy điểm N sao cho AN=BM.Kẻ BP//KM(P thuộc tâm O) a) Chứng minh ANKP là hình bình hành
BP//KM
=>PK=BM
=>PK=AN
mà PK//AN
nên ANKP là hình bình hành
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và điểm A bất kỳ thuộc đường tròn (O). Trên tiếp tuyến tại A của đường tròn (O) lấy một điểm M sao cho MA2R. Từ M vẽ tiếp tuyến MB với (O) (B là tiếp điểm, B khác A); OM cắt AB tại Ha) Chứng minh tứ giác OAMB là tứ giác nội tiếp và OM vuông góc ABb) Vẽ đường kính BD của đường tròn (O); MD cắt đường tròn (O) tại E (E khác D).Chứng minh MB2MA2ME.MDc) Tính góc MHEd) Từ A vẽ AF vuông góc BD (F thuộc BD); tia BE cắt đường thẳng AF tại K.Chứng minh A là trung điểm của K...
Đọc tiếp
Cho đường tròn tâm O bán kính R và điểm A bất kỳ thuộc đường tròn (O). Trên tiếp tuyến tại A của đường tròn (O) lấy một điểm M sao cho MA=2R. Từ M vẽ tiếp tuyến MB với (O) (B là tiếp điểm, B khác A); OM cắt AB tại H
a) Chứng minh tứ giác OAMB là tứ giác nội tiếp và OM vuông góc AB
b) Vẽ đường kính BD của đường tròn (O); MD cắt đường tròn (O) tại E (E khác D).Chứng minh MB2=MA2=ME.MD
c) Tính góc MHE
d) Từ A vẽ AF vuông góc BD (F thuộc BD); tia BE cắt đường thẳng AF tại K.Chứng minh A là trung điểm của KF
Cho đường tròn tâm O bán kính R và đường thẳng (d) không qua O, cắt đường tròn (O) tại 2 điểm A, B. Lấy điểm M bất kì trên tia đối của tia BA, qua M kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là tiếp điểm)
1. Chứng minh tứ giác MCOD nội tiếp trong một đường tròn.
2. Gọi H là trung điểm của AB. Chứng minh HM là phân giác của góc CHD
Cho đường tròn tâm O đường kính AB bán kính R ,trên tia đối AB lấy C sao cho AC bằng R .Kẻ d vuông góc BC tại C. Gọi D là trung điểm của OA, qua D vẽ dây EF bất kì với O(EF không phải đường kính).tia BE cắt D tại M.tia BF cắt d tại N
a)chứng minh MCAE nội tiếp
b) chứng minh BE.BM=BF.BN
c) Khi EF vuông góc AB .tính MN
Cho đường tròn (O,R) đường kính AB. Bán kính CO vuông góc với AB, M là điểm bất kì trên cung nhỏ AC ( M khác A và C), BM cắt AC tại H. Gọi K là hình chiếu của H trên AB1, Chứng minh CBKH là tứ giác nội tiếp và ACMACK2,Trên đoạn thẳng BM lấy điểm E sao cho BEAM. Chứng minh tam giác ECM vuông cân tại C3, Gọi d, là tiếp tuyến của (O) tại điểm A. Cho P là 1 điểm nằm trên d sao cho hai điểm P,C nằm trên cùng một mặt phẳng bờ AB và AP.MB/AMR. Chứng minh đường thẳng PB đi qua trung điểm của HK
Đọc tiếp
Cho đường tròn (O,R) đường kính AB. Bán kính CO vuông góc với AB, M là điểm bất kì trên cung nhỏ AC ( M khác A và C), BM cắt AC tại H. Gọi K là hình chiếu của H trên AB
1, Chứng minh CBKH là tứ giác nội tiếp và ACM=ACK
2,Trên đoạn thẳng BM lấy điểm E sao cho BE=AM. Chứng minh tam giác ECM vuông cân tại C
3, Gọi d, là tiếp tuyến của (O) tại điểm A. Cho P là 1 điểm nằm trên d sao cho hai điểm P,C nằm trên cùng một mặt phẳng bờ AB và AP.MB/AM=R. Chứng minh đường thẳng PB đi qua trung điểm của HK
1) Dễ thấy \(\widehat{HCB}=\widehat{ACB}=90^o\)
tứ giác CBKH có \(\widehat{HKB}=\widehat{HCB}=90^o\)nên là tứ giác nội tiếp
\(\Rightarrow\widehat{HCK}=\widehat{HBK}\)( 1 )
Mà \(\widehat{ACM}=\widehat{ABM}=\frac{1}{2}sđ\widebat{AM}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{ACM}=\widehat{ACK}\)
2) Xét \(\Delta AMC\)và \(\Delta BEC\)có :
AM = BE ; AC = BC ; \(\widehat{MAC}=\widehat{CBE}=\frac{1}{2}sđ\widebat{MC}\)
\(\Rightarrow\Delta AMC=\Delta BEC\)( c.g.c )
\(\Rightarrow MC=EC\)
Ta có : \(\widehat{CMB}=\frac{1}{2}sđ\widebat{BC}=45^o\)
Suy ra \(\Delta ECM\)vuông cân tại C
3) Ta có : \(\frac{AP.MB}{AM}=R=OB\Rightarrow\frac{AP}{MA}=\frac{OB}{MB}\)
Xét \(\Delta APM\)và \(\Delta OBM\), ta có :
\(\frac{AP}{MA}=\frac{OB}{MB}\); \(\widehat{PAM}=\widehat{MBO}=\frac{1}{2}sđ\widebat{AM}\)
\(\Rightarrow\Delta APM\approx\Delta BOM\left(c.g.c\right)\)
\(\Rightarrow\Delta APM\)cân tại P ( vì \(\Delta BOM\)cân tại O )
\(\Rightarrow PA=PM\)
Gọi giao điểm của BM và ( d ) là F ; giao điểm của BP với HK là I
Xét tam giác vuông AMF có PA = PM nên PA = PM = PF
Theo định lí Ta-let, ta có :
\(\frac{HI}{FP}=\frac{BI}{BP}=\frac{KI}{AP}\Rightarrow HI=KI\)
vì vậy PB đi qua trung điểm của HK