Cho △ABC vuông tại A có điểm D nằm giữa A và B, điểm E nằm giữa A và C. So sánh DE và BC

Những câu hỏi liên quan
cho tam giác ABC vuông tại A
E là điêm nằm giữa A và C hãy so sánh độ dài BA,BE,BC
D là điểm nằm giữa A và B hãy so sánhđộ dài DE và BC
e nằm giữa A và C nên AE< AC \(\Rightarrow\)BE<BC( đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
do tam giác ABC vuông tại A nên BA là đường vuông góc nên BA là đường thẳng ngắn nhất \(\Rightarrow\)BA<BE
Vậy BA<BE<BC
làm tương tự phần b
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A , điểm D nằm giữa B và C ( AD không vuông góc với BC ) . Gọi E và F là hình chiếu của B và C trên AD a) So sánh BC với BE + CF b) Tam giác ABE tam giác CAF c)BE mũ 2 + CF mũ 2 AB mũ 2 d) gọi m là trung điểm của BC , chứng minh tam giác M...
Đọc tiếp
Cho tam giác ABC vuông cân tại A , điểm D nằm giữa B và C ( AD không vuông góc với BC ) . Gọi E và F là hình chiếu của B và C trên AD a) So sánh BC với BE + CF b) Tam giác ABE = tam giác CAF c)BE mũ 2 + CF mũ 2 = AB mũ 2 d) gọi m là trung điểm của BC , chứng minh tam giác MBE = tam giác MAF e ) Tam giác MEF vuông cân
Cho tam giác ABC vuông tại A, điểm H nằm giữa A và C. So sánh BH và BC. E cần gấp ạ
Cho tam giác ABC có góc A > 90 độ, điểm D nằm giữa A và C.
a) CM rằng BA < BD < BC.
b) Trên cạnh AB lấy điểm E (E khác A, E khác B). So sánh DE và BC.
a ) Ta có : gócA = 90o
=> gócD1 và gócB1 đều là góc nhọn ( vì trong tam giác vuông thì có một góc vuông và 2 góc nhọn )
=> gócD1 < 90o ( Số đo của góc nhọn luôn luôn bé hơn số đo của góc vuông )
=> gócD1 < gócA ( 1 )
Mà : gócD1 là góc đối diện của BA
( 2 )
: gócA là góc đối diện của BD
Từ ( 1 ) và ( 2 ) suy ra : BA < BD ( Vì trong một tam giác cạnh đối diện với góc lớn hơn thì có số đo lớn hơn ) ( 3 )
Ta có : gócD1 + gócD2 = gócADC ( DB nằm giữa DA và DC )
=> gócD2 = gócADC - gócD1 = góc bẹt - góc nhọn = góc tù ( Vì góc bẹt = 180o , góc nhọn bé hơn 90o )
=> gócD2 > 90o ( Vì số đo của góc tù lớn hơn góc vuông )
=> gócD2 > gócA ( 4 )
Mà : gócA là góc đối diện với BD
( 5 )
: gócD2 là góc đối diện với BC
Từ ( 4 ) và ( 5 ) suy ra : BC > BD ( Vì trong tam giác cạnh đối diện với góc có số đo lớn hơn thì lớn hơn ) ( 6 )
Từ ( 3 ) và ( 6 ) suy ra : BA < BD < BC ( điều phải chứng minh )
b ) Ta có : gócD2 > gócA ( cmt ) ( 7 )
Mà : gócD2 là góc đối diện với BC
( 8 )
: gócA là góc đối diện với DE
Từ ( 7 ) và ( 8 ) suy ra : BC > DE ( Vì trong tam giác cạnh đối diện với ............................................ )
Học tốt !
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A tù, điểm D nằm giữa A và B, điểm E nằm giữa A và C. Chứng minh BC > DE
Bạn tham khảo ở đây nhé!!
https://h.vn/hoi-dap/question/269901.html
hok tốt!!
~
Vì góc bac là góc tú nên độ dài ab lớn
Mà d nằm giữa ba và e năm giữa ac nên
De<bc
Cho tam giác ABC vuông tại B.Trên cạnh BC lấy các điểm D và E ( D nằm giữa B và E)
a) So sánh các độ dài các đoạn thẳng AB,AD,AE,AC
Vì ΔBAC vuông tại B
nên AB<AC
góc ACB<90 độ
=>góc ACD>90 độ
=>AC<AD
góc ACD>90 độ
=>góc CDA<90 độ
=>góc ADE>90 độ
=>AD<AE
=>AB<AC<AD<AE
Đúng 1
Bình luận (1)
Cho tam giác ABC có góc A tù, trên cạnh AC lần lượt lấy điểm D, E, F sao cho D nằm giữa A và E; E nằm giữa D và F; F nằm giữa E và C. So sánh các đoạn thẳng BA, BD, BE, BF, BC
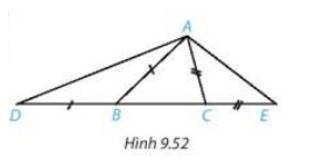
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, điểm H nằm giữa A và C. So sánh BH và BC.
















