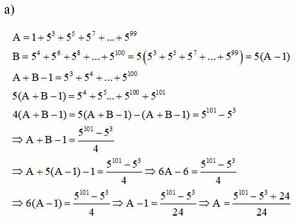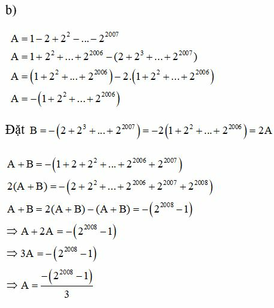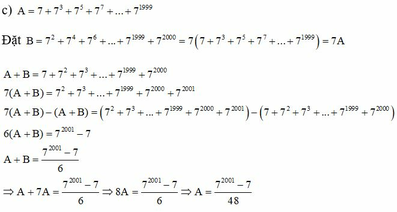A=(7+73)+(75+77)+....+(71997+71999)

A=7.(1+72)+75.(1+72)+....+71997.(1+72)

A=7.50+75.50+79.50+.....+71997.50

=>A chia hết cho 5 (1)

A=(7+73+75+....+71999)=7.(70+72+74+....+71998)

=>A chia hết cho 7 (2)

Mà ƯCLN(5;7)=1=>A chia hết cho 35

Ban kia lam dung roi

Lời giải:

Hiển nhiên $A\vdots 7$ do các số hạng đều chia hết cho 7.

Lại có:

$A=(7+7^3)+(7^5+7^7)+....+(7^{1997}+7^{1999})$

$=7(1+7^2)+7^5(1+7^2)+...+7^{1997}(1+7^2)$
$=(1+7^2)(7+7^5+...+7^{1997})$
$=50(7+7^5+...+7^{1997})\vdots 5$

Vậy $A\vdots 7, A\vdots 5$. Mà $(7,5)=1$

$\Rightarrow A\vdots 35$

Xem lại đề không rõ qui luật

a,  A = 1 + 5 3 + 5 5 + 5 7 + . . . + 5 99

B = 5 4 + 5 6 + 5 8 + . . . + 5 100 =  5 . ( 5 3 + 5 5 + 5 7 + . . . + 5 99 ) = 5(A – 1)

A + B – 1 =  5 3 + 5 4 + . . . + 5 100

5(A + B – 1) =  5 4 + 5 5 + . . . + 5 100 + 5 101

4(A + B – 1) = 5(A + B – 1) – (A + B – 1) =  5 101 - 5 3

=> A + B – 1 =  5 101 - 5 3 4

=> A + 5(A – 1) –1 =  5 101 - 5 3 4 => 6A – 6 =  5 101 - 5 3 4

=> A – 1 =  5 101 - 5 3 24

=> A =  5 101 - 5 3 + 24 24

b,  A = 1 - 2 + 2 2 - . . . - 2 2007

A = 1 + 2 2 + . . . + 2 2006 - 2 + 2 3 + . . . + 2 2007

A = ( 1 + 2 2 + . . . + 2 2006 ) - 2 . 1 + 2 2 + . . . + 2 2006

A = - 1 + 2 2 + . . . + 2 2006

Đặt  B = - 2 + 2 3 + . . . + 2 2007 =  - 2 . 1 + 2 2 + . . . + 2 2006 = 2A

A + B =  - 1 + 2 + 2 2 + . . . + 2 2006 + 2 2007

2(A+B) =  - 2 + 2 2 + . . . + 2 2006 + 2 2007 + 2 2008

A+B = 2(A+B)–(A+B) =  - 2 2008 - 1

=> A+2A =  - 2 2008 - 1

=> 3A =  - 2 2008 - 1

=> A =  - ( 2 2008 - 1 ) 3

c,  A = 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999

Đặt B =  7 2 + 7 4 + 7 6 + . . . + 7 1999 + 7 2000 =  7 ( 7 + 7 3 + 7 5 + 7 7 + . . . + 7 1999 ) = 7A

A+B =  7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000

7(A+B) =  7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001

7(A+B) – (A+B) =  ( 7 2 + 7 3 + . . . + 7 1999 + 7 2000 + 7 2001 )  –  ( 7 + 7 2 + 7 3 + . . . + 7 1999 + 7 2000 )

6(A+B) =  7 2001 - 7

A+B =  7 2001 - 7 6

=> A + 7A =  7 2001 - 7 6 => 8A =  7 2001 - 7 6 => A =  7 2001 - 7 48

\(A=7+7^2+7^3+...+7^{120}\\ A=\left(7+7^2+7^3\right)+...+\left(7^{118}+7^{119}+7^{120}\right)\\ A=7\times\left(1+7+7^2\right)+...+7^{118}\times\left(1+7+7^2\right)\\ A=7\times57+7^4\times57+...+7^{118}\times57\\ A=57\times\left(7+7^4+...+7^{118}\right)\\ \Rightarrow A⋮57\)

\(A=7\left(1+7+7^2\right)+7^4\left(1+7+7^2\right)+...+7^{118}\left(1+7+7^2\right)=7.57+7^4.57+...+7^{118}.57=57\left(7+7^4+...+7^{118}\right)⋮57\)

Lời giải:
$A=(7+7^2+7^3)+(7^4+7^5+7^6)+....+(7^{118}+7^{119}+7^{120})$
$=7(1+7+7^2)+7^4(1+7+7^2)+...+7^{118}(1+7+7^2)$

$=7.57+7^4.57+...+7^{118}.57$

$=57(7+7^4+...+7^{118})\vdots 57$ 

Ta có đpcm.

Bài 1:

\(a,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\\ A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)=3\left(2+...+2^{2009}\right)⋮3\\ A=\left(2+2^2+2^3\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{2008}\right)=7\left(2+...+2^{2008}\right)⋮7\)

\(b,\left(\text{sửa lại đề}\right)B=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\\ B=\left(1+3\right)\left(3+3^3+...+3^{2009}\right)=4\left(3+3^3+...+3^{2009}\right)⋮4\\ B=\left(3+3^2+3^3\right)+...+\left(3^{2008}+3^{2009}+3^{2010}\right)\\ B=\left(1+3+3^2\right)\left(3+...+3^{2008}\right)=13\left(3+...+3^{2008}\right)⋮13\)

Bài 2:

\(a,\Rightarrow2A=2+2^2+...+2^{2012}\\ \Rightarrow2A-A=2+2^2+...+2^{2012}-1-2-2^2-...-2^{2011}\\ \Rightarrow A=2^{2012}-1>2^{2011}-1=B\\ b,A=\left(2020-1\right)\left(2020+1\right)=2020^2-2020+2020-1=2020^2-1< B\)

đúng rùi

 á à thg hếu cx hỏi trên này cơ à XDDD