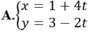
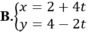
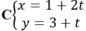
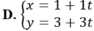
Gọi M( 1; 3) là trung điểm của AB.

Ta có 

Gọi d  là đường thẳng trung trực của AB thì d qua M( 1;3)  và nhận  làm VTCP nên có phương trình tham số là:

Chọn A.

Đường cao AH là đường thẳng đi qua A(1; 4) và vuông góc với BC.

 = (3; 3)  =>   ⊥  nên  nhận vectơ    = (3; 3) làm vectơ pháp tuyến và có phương trình tổng quát:

AH : 3(x – 1) + 3(y -4) = 0

3x + 3y – 15 = 0

=> x + y – 5 = 0

Gọi M là trung điểm BC ta có M (; )

Trung tuyến AM là đường thẳng đi qua hai điểm A, M. Theo các viết phương trình đường thẳng đi qua hai điểm trong câu a) ta viết được:

AM : x + y – 5 = 0

X-Y-5=0

......

\(\overrightarrow{AB}=\left(4;4\right)=4\left(1;1\right)\)

Đường trung trực của AB vuông góc AB nên nhận \(\left(1;-1\right)\) là 1 vtcp

Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)

Phương trình trung trực AB qua M có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=3-t\end{matrix}\right.\)

Chúc bạn học tốt!

Ai giúp mình với 😥

a/ Giả sử phương trình AB là \(y=ax+b\)

\(A\left(2;4\right)\in AB\Rightarrow4=2a+b\text{ (1)}\)

\(B\left(4;6\right)\in AB\Rightarrow6=4a+b\text{ (2)}\)

Từ (1) và (2) suy ra \(a=1;\text{ }b=2\)

\(AB:y=x+2\)

Trung điểm của AB là \(M\left(\frac{2+4}{2};\text{ }\frac{4+6}{2}\right)\text{ hay }M\left(3;5\right)\)

Gọi phương trình trung trực AB là \(d:y=a_1x+b_1\)

d vuông góc với AB nên \(a'.a=-1\Rightarrow a'=-\frac{1}{a}=-\frac{1}{1}=-1\)

\(\Rightarrow d:y=-x+b_1\)

\(M\in d\Rightarrow5=-3+b_1\Rightarrow b_1=8\)

\(\text{Vậy }d:y=-x+8\)

b/

Làm tương tự câu a, sau đó đồng nhất hệ số \(2m+3=a_1;\text{ }-3n+4=b_1\)

a)  Phương trình đường thẳng AB đi qua 2 điểm A và B là: \(\frac{{x - 1}}{{ - 1 - 1}} = \frac{{y - 3}}{{ - 1 - 3}} \Leftrightarrow \frac{{x - 1}}{{ - 2}} = \frac{{y - 3}}{{ - 4}} \Leftrightarrow 2x - y + 1 = 0\)

 Phương trình đường thẳng AC đi qua 2 điểm A và C là: \(\frac{{x - 1}}{{5 - 1}} = \frac{{y - 3}}{{ - 3 - 3}} \Leftrightarrow \frac{{x - 1}}{4} = \frac{{y - 3}}{{ - 6}} \Leftrightarrow 3x + 2y - 9 = 0\)

 Phương trình đường thẳng BC đi qua 2 điểm B và C là:

\(\frac{{x + 1}}{{5 + 1}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow \frac{{x + 1}}{6} = \frac{{y + 1}}{{ - 2}} \Leftrightarrow x + 3y + 4 = 0\)

b)  Gọi d là đường trung trực của cạnh AB.

 Lấy N là trung điểm của AB, suy ra \(N\left( {0;1} \right)\).

 Do \(d \bot AB\) nên ta có vecto pháp tuyến của d là: \(\overrightarrow {{n_d}}  = \left( {1;2} \right)\)

 Vậy phương trình đường thẳng d đi qua N có vecto pháp tuyến \(\overrightarrow {{n_d}}  = \left( {1;2} \right)\) là:

\(1\left( {x - 0} \right) + 2\left( {y - 1} \right) = 0 \Leftrightarrow x + 2y - 2 = 0\)

c)  Do AH vuông góc với BC nên vecto pháp tuyến của AH là \(\overrightarrow {{n_{AH}}}  = \left( {3; - 1} \right)\)

 Vậy phương trình đường cao AH đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AH}}}  = \left( {3; - 1} \right)\)là: \(3\left( {x - 1} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow 3x - y = 0\)

 Do M là trung điểm BC nên \(M\left( {2; - 2} \right)\). Vậy ta có: \(\overrightarrow {AM}  = \left( {1; - 5} \right) \Rightarrow \overrightarrow {{n_{AM}}}  = \left( {5;1} \right)\)

 Phương trình đường trung tuyến AM đi qua điểm A có vecto pháp tuyến \(\overrightarrow {{n_{AM}}}  = \left( {5;1} \right)\) là:

\(5\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 5x + y - 8 = 0\)

a.Phương trình d: \(\left\{{}\begin{matrix}x=1+t\\y=-2-2t\end{matrix}\right.\)

b. Gọi H là trung điểm AB \(\Rightarrow H\left(\dfrac{1}{2};1\right)\)

\(\overrightarrow{BA}=\left(1;-6\right)\Rightarrow\) trung trực AB nhận \(\left(6;1\right)\) là 1 vtcp

Phương trình: \(\left\{{}\begin{matrix}x=\dfrac{1}{2}+6t\\y=1+t\end{matrix}\right.\)

c. \(\overrightarrow{BA}=\left(1;-6\right)\) nên AB nhận (1;-6) là 1 vtcp

Phương trình AB: \(\left\{{}\begin{matrix}x=1+t\\y=-2-6t\end{matrix}\right.\)

d. Gọi M là trung điểm  AC \(\Rightarrow M\left(\dfrac{7}{2};\dfrac{1}{2}\right)\) \(\Rightarrow\overrightarrow{MH}=\left(3;-\dfrac{1}{2}\right)=\dfrac{1}{2}\left(6;-1\right)\)

Phương trình MH: \(\left\{{}\begin{matrix}x=\dfrac{7}{2}+6t\\y=\dfrac{1}{2}-t\end{matrix}\right.\)