tam giác abc đều các cạnh là 2a có trọng tâm g khi đó vecto GA+GB-GC BẰNG

Những câu hỏi liên quan
Cho tam giác ABC có G là trọng tâm. Chọn khẳng định sai trong các khẳng định sau
A. vecto MA vecto MB vecto MC= 3 vecto MG
B. vecto GA vecto GB vecto GC= vecto 0
C. vecto GA= vecto GB= vecto GC
D. |vecto GA vecto GB vecto GC|=0
Cho tam giác ABC vuông tại A có AB a; BC 2a và G là trọng tâm. Tính giá trị của biểu thức
G
A
→
.
G
B
→
+
G
B
→
.
G
C
→
+
G
C
→
....
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
Tính giá trị của biểu thức G A → . G B → + G B → . G C → + G C → . G A
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
Chọn C.
Vì ![]() nên
nên
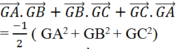
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
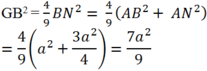
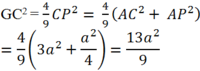
Suy ra
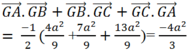
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a, gọi G là trọng tâm. Tính T: \(\overrightarrow{GA}.\overrightarrow{BC}+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)
\(T=\overrightarrow{GA}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}-\overrightarrow{GA}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}-\overrightarrow{GB}\right)\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}+\overrightarrow{AG}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}+\overrightarrow{BG}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{BA}\)
\(=0\)
Đúng 1
Bình luận (0)
Gọi vecto GA + GB+GC =veto 0. CMR G là trọng tâm tam giác ABC
* cái này là công thức rồi bn o cần chứng minh đâu
công thức : cho tam giác ABC ; nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Gọi M trung điểm BC
G đối xứng D qua M
=> tứ giác BGCD là hình bình hành
=> GD=2.GM (Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AG = 2.GM ( \(\dfrac{AG}{GM}=\dfrac{2}{1},GA=\dfrac{2}{3}AM\) )
⇒ AG=GD
Mặt khác, G ϵ AD
⇒\(\overrightarrow{AG}=\overrightarrow{GD}\)
Ta có \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (Quy tắc hình bình hành)
Nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}\) = \(\overrightarrow{GD}+\overrightarrow{GA}\)
Mà \(\overrightarrow{AG}=\overrightarrow{GD}\) (cmt)
⇒\(\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{AG}-\overrightarrow{AG}=\overrightarrow{O}\)
Đúng 0
Bình luận (0)
giúp mình với các thần đồng !!
Cho G là trọng tâm tam giác ABC. CM:
a) vecto GA + vecto GB + vecto GC= vecto 0
b) vecto MA + vecto MB + vecto MC= 3 vecto MG ( với mọi M)
a: Gọi M là trung điểm của AB
Xét ΔABC có
G là trọng tâm
M là trung điểm của AB
Do đó: CG=2/3CM
=>CG=2GM
=>\(\overrightarrow{CG}=2\overrightarrow{GM}\)
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)
\(=2\overrightarrow{GM}+\overrightarrow{GC}\)
\(=\overrightarrow{CG}+\overrightarrow{GC}=\overrightarrow{0}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
\(=3\cdot\overrightarrow{MG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3\cdot\overrightarrow{MG}\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh a, đường cao AH, trọng tâm G. Tính:
a, |AC|, |AB + AH|, |AB - AH|
b, |GB|, |GA + GB|, |GA + GB + GC|
Tam giác ABC đều cạnh là 8cm. G là trọng tâm của tam giác ABC, trung tuyến AD, BE, CF.
a/ Tính AD, CG
b/ Chứng minh GA = GB + GC
a: AD=BE=CF=8*căn 3/2=4*căn 3(cm)
CG=2/3*4*căn 3=8/3*căn 3(cm)
b: Vì ΔABC đều có G là trọng tâm
nên G là tâm đường tròn ngoại tiếp
=>GA=GB=GC
Đúng 0
Bình luận (0)
chứng minh gấp hộ tui với
Cho tam giác ABC:
a) Nếu G là trọng tâm tam giác ABC thì vecto GA+ vecto GB+ vecto GC= vecto 0
b) Nếu vecto IA+ vecto IB + vecto IC = vecto 0 thì I là trọng tâm tam giác ABC
TUI CẦN GẤP CHO BUỔI DỰ GIỜ NGÀY MAI NÊN AI ĐÓ GIÚP TUI ZỚIIII~~~
mk bận đi ch nên chỉ tạm câu a nha
vẽ 3 đường trung tuyến AD ; BE ; CF
VT =
\(GA+GB+GC\) ( nhớ thêm dấu vec tơ nha )
\(=-\frac{2}{3}AD-\frac{2}{3}BE-\frac{2}{3}CF\)
\(=-\frac{2}{3}\cdot\frac{1}{2}\left(AB+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(BA+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(CA+CB\right)\) ( quy tắc hình bình hành )
\(=-\frac{1}{3}\left(AB+AC\right)-\frac{1}{3}\left(BA+BC\right)-\frac{1}{3}\left(CA+CB\right)\)
\(=-\frac{1}{3}AB-\frac{1}{3}AC-\frac{1}{3}BA-\frac{1}{3}BC-\frac{1}{3}CA-\frac{1}{3}CB\)
\(=0=VP\)
Cho tam △ABC đều có G là trọng tâm. Và M là trung điểm BC. Tìm các vecto: GB+GC, AG+CB, AB+MC, AB+GB+GC




















