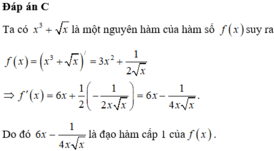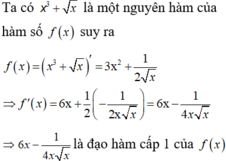hàm số là gì?

Những câu hỏi liên quan
a,đồ thị hàm số là gì? đồ thị hàm số y=ax(a khác 0) là gì?
b,vẽ trên cùng một tọa độ Oxy đồ thị hàm số y=3x;y=-3x
Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
Đúng 0
Bình luận (0)
Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
Đúng 0
Bình luận (0)
kết bạn đi nha
Biết rằng
x
3
+
x
là một nguyên hàm của hàm số
f
x
. Hỏi đa thức
6
x
-
1
4
x
x
là gì của hàm số ? A. Là hàm số f(x) B. Đạo hàm cấp 3 C. Đạo hàm cấp 2 D. Đạo hàm cấp 1
Đọc tiếp
Biết rằng x 3 + x là một nguyên hàm của hàm số f x . Hỏi đa thức 6 x - 1 4 x x là gì của hàm số ?
A. Là hàm số f(x)
B. Đạo hàm cấp 3
C. Đạo hàm cấp 2
D. Đạo hàm cấp 1
Đáp án D
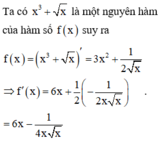
Do đó 6 x - 1 4 x x là đạo hàm cấp 1 của f(x).
Đúng 0
Bình luận (0)
Biết rằng
x
3
+
x
là một nguyên hàm của hàm số
f
x
. Hỏi đa thức
6
x
−
1
4
x
x
là gì cuả hàm số
f
x
? A. Là hàm số
f
x
B. Đạo hàm cấp 2 C. Đạo hàm cấp 1 D. Đạo hàm cấp 3
Đọc tiếp
Biết rằng x 3 + x là một nguyên hàm của hàm số f x . Hỏi đa thức 6 x − 1 4 x x là gì cuả hàm số f x ?
A. Là hàm số f x
B. Đạo hàm cấp 2
C. Đạo hàm cấp 1
D. Đạo hàm cấp 3
Biết rằng
x
3
+
x
là một nguyên hàm của hàm số f(x). Hỏi đa thức
6
x
-
1
4
x
x
là gì của hàm số f(x) ?
Đọc tiếp
Biết rằng x 3 + x là một nguyên hàm của hàm số f(x). Hỏi đa thức 6 x - 1 4 x x là gì của hàm số f(x) ?
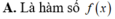
![]()
![]()
hàm số là gì ?
Hàm số là gì?
Trong toán học, khái niệm hàm số (hay hàm) được hiểu tương tự như khái niệm ánh xạ. Nếu như ánh xạ được định nghĩa là một qui tắc tuơng ứng áp dụng lên hai tập hợp bất kỳ (còn được gọi là tập nguồn và tập đích), mà trong đó mỗi phần tử của tập hợp này (tập hợp nguồn) tương ứng với một và chỉ một phần tử thuộc tập hợp kia (tập hợp đích), thì ta hoàn toàn có thể coi hàm số là một trường hợp đặc biệt của ánh xạ, khi tập nguồn và tập đích đều là tập hợp số.
Ví dụ một hàm số f xác định trên tập hợp số thực R được miêu tả bằng biểu thức:y = x2 - 5 sẽ cho tương ứng mỗi số thực x với một số thực y duy nhất nhận giá trị là x2 - 5, như vậy 3 sẽ tương ứng với 4. Khi hàm f đã được xác định, ta có thể viết f(3) = 4.
Đôi khi chữ hàm được dùng như cách gọi tắt thay cho hàm số. Tuy nhiên trong các trường hợp sử dụng khác, hàm mang ý nghĩa tổng quát của ánh xạ, như trong lý thuyết hàm. Các hàm hay ánh xạ tổng quát có thể là liên hệ giữa các tập hợp không phải là tập số. Ví dụ có thể định nghĩa một hàm là qui tắc cho tương ứng mỗi hãng xe với tên quốc gia xuất xứ của nó, chẳng hạn có thể viết Xuất_xứ(Honda) = N
Ví dụ một hàm số f xác định trên tập hợp số thực R được miêu tả bằng biểu thức:y = x2 - 5 sẽ cho tương ứng mỗi số thực x với một số thực y duy nhất nhận giá trị là x2 - 5, như vậy 3 sẽ tương ứng với 4. Khi hàm f đã được xác định, ta có thể viết f(3) = 4.
Đôi khi chữ hàm được dùng như cách gọi tắt thay cho hàm số. Tuy nhiên trong các trường hợp sử dụng khác, hàm mang ý nghĩa tổng quát của ánh xạ, như trong lý thuyết hàm. Các hàm hay ánh xạ tổng quát có thể là liên hệ giữa các tập hợp không phải là tập số. Ví dụ có thể định nghĩa một hàm là qui tắc cho tương ứng mỗi hãng xe với tên quốc gia xuất xứ của nó, chẳng hạn có thể viết Xuất_xứ(Honda) = N
Đúng 0
Bình luận (0)
nếu đại lượng Y phụ thuộc vào đại lượng thay đổi X sao cho mỗi giá trị của X ta chỉ nhận được một giá trị tương ứng của Y thì Y là biến số và X là hàm số
Đúng 0
Bình luận (0)
Hàm số là gì
Trong toán học, khái niệm hàm số (hay hàm) được hiểu tương tự như khái niệm ánh xạ. Thực chất hàm số chỉ là trường hợp đặc biệt của ánh xạ. Nếu như ánh xạ được định nghĩa là một quy tắc tương ứng áp dụng lên hai tập hợp bất kỳ (còn được gọi là tập nguồn và tập đích), mà trong đó mỗi phần tử của tập hợp này (tập hợp nguồn) tương ứng với một và chỉ một phần tử thuộc tập hợp kia (tập hợp đích), thì ta hoàn toàn có thể coi hàm số là một trường hợp đặc biệt của ánh xạ, khi tập nguồn và tập đích đều là tập hợp số.
Đúng 0
Bình luận (0)
Trong toán học, khái niệm hàm số (hay hàm) được hiểu tương tự như khái niệm ánh xạ. Thực chất hàm số chỉ là trường hợp đặc biệt của ánh xạ. Nếu như ánh xạ được định nghĩa là một quy tắc tương ứng áp dụng lên hai tập hợp bất kỳ (còn được gọi là tập nguồn và tập đích), mà trong đó mỗi phần tử của tập hợp này (tập hợp nguồn) tương ứng với một và chỉ một phần tử thuộc tập hợp kia (tập hợp đích), thì ta hoàn toàn có thể coi hàm số là một trường hợp đặc biệt của ánh xạ, khi tập nguồn và tập đích đều là tập hợp số.
Ví dụ một hàm số f xác định trên tập hợp số thực R bằng biểu thức: y = x2 - 5 sẽ cho tương ứng mỗi số thực x với một số thực y duy nhất nhận giá trị là x2 - 5, như vậy 3 sẽ tương ứng với 4. Khi hàm f được xác định, ta có thể viết f(3) = 4.
Đôi khi chữ hàm được dùng như cách gọi tắt thay cho hàm số. Tuy nhiên trong các trường hợp sử dụng khác, hàm mang ý nghĩa tổng quát là ánh xạ, như trong lý thuyết hàm. Các hàm hay ánh xạ tổng quát có thể là liên hệ giữa các tập hợp không phải là tập số. Ví dụ có thể định nghĩa một hàm là quy tắc cho tương ứng mỗi hãng xe với tên quốc gia xuất xứ của nó, chẳng hạn có thể viết Xuất_xứ(Honda) = Nhật.
Kí hiệu hàm số bắt nguồn từ tiếng Anh của từ function, có nghĩa là phụ thuộc, chẳng hạn nghĩa là đại lượng y phụ thuộc vào x một lượng là căn bậc 2 của x, khi đó ta kí hiệu {\displaystyle f(x)={\sqrt {x}}}
Đúng 0
Bình luận (0)
Trong toán học, khái niệm hàm số (hay hàm) được hiểu tương tự như khái niệm ánh xạ. Thực chất hàm số chỉ là trường hợp đặc biệt của ánh xạ. Nếu như ánh xạ được định nghĩa là một quy tắc tương ứng áp dụng lên hai tập hợp bất kỳ (còn được gọi là tập nguồn và tập đích), mà trong đó mỗi phần tử của tập hợp này (tập hợp nguồn) tương ứng với một và chỉ một phần tử thuộc tập hợp kia (tập hợp đích), thì ta hoàn toàn có thể coi hàm số là một trường hợp đặc biệt của ánh xạ, khi tập nguồn và tập đích đều là tập hợp số.
Ví dụ một hàm số f xác định trên tập hợp số thực R bằng biểu thức: y = x2 - 5 sẽ cho tương ứng mỗi số thực x với một số thực y duy nhất nhận giá trị là x2 - 5, như vậy 3 sẽ tương ứng với 4. Khi hàm f được xác định, ta có thể viết f(3) = 4.
Đôi khi chữ hàm được dùng như cách gọi tắt thay cho hàm số. Tuy nhiên trong các trường hợp sử dụng khác, hàm mang ý nghĩa tổng quát là ánh xạ, như trong lý thuyết hàm. Các hàm hay ánh xạ tổng quát có thể là liên hệ giữa các tập hợp không phải là tập số. Ví dụ có thể định nghĩa một hàm là quy tắc cho tương ứng mỗi hãng xe với tên quốc gia xuất xứ của nó, chẳng hạn có thể viết Xuất_xứ(Honda) = Nhật.
Kí hiệu hàm số bắt nguồn từ tiếng Anh của từ function, có nghĩa là phụ thuộc, chẳng hạn nghĩa là đại lượng y phụ thuộc vào x một lượng là căn bậc 2 của x, khi đó ta kí hiệu {\displaystyle f(x)={\sqrt {x}}}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hàm số là gì?
ê cho tui hỏi hàm số là gì
Tham khảo Trong toán học, một hàm số hay hàm là một quan hệ hai ngôi giữa hai tập hợp liên kết mọi phần tử của tập hợp đầu tiên với đúng một phần tử của tập hợp thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực.
Đúng 0
Bình luận (2)
Tham khảo/:
Trong toán học, một hàm số hay hàm là một quan hệ hai ngôi giữa hai tập hợp liên kết mọi phần tử của tập hợp đầu tiên với đúng một phần tử của tập hợp thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời