a) -12,13; -2,4; -2,3; 0,5; 2,4

b) 2,999; 2,9; -2,9; -2,999

a) -12,13; -2,4; -2,3; 0,5; 2,4

b) 2,999; 2,9; -2,9; -2,999

a) - 12,13; - 2,4; - 2,3; 0,5; 2,4

b) 2,999; 2,9; - 2,9; - 2,999

a) -12,13; -2,4; -2,3; 0,5; 2,4

b) 2,999; 2,9; -2,9; -2,999

 Ta có: \(\frac{{ - 25}}{{ - 6}} = \frac{{25}}{6} = 4\frac{1}{6}\)

Nên : \(3 < 3\frac{5}{6} < 4\frac{1}{6}\)

Suy ra các sắp xếp các số theo thứ tự từ bé đến lớn \(\frac{{ - 9}}{4} < 3 < 3\frac{5}{6} < 4\frac{1}{6}\)

 -15; -1; 0; 3; 5;8

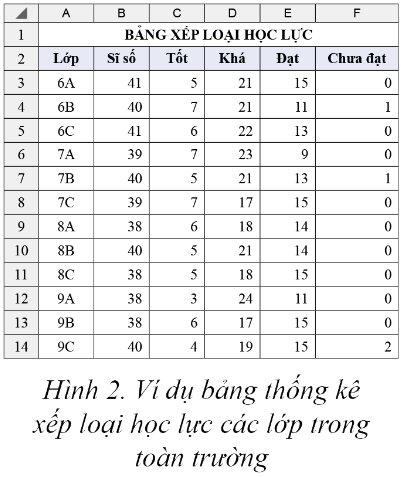
- Sắp xếp theo thứ tự tăng dần của cột Tốt

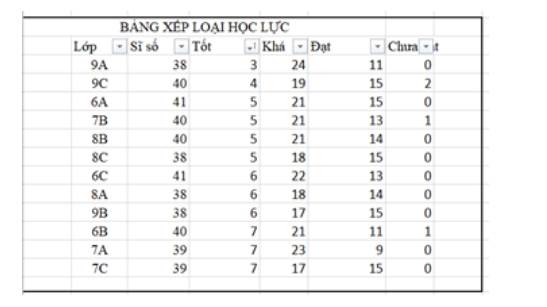
- Sắp xếp theo thứ tự giảm dần của cột Sĩ số

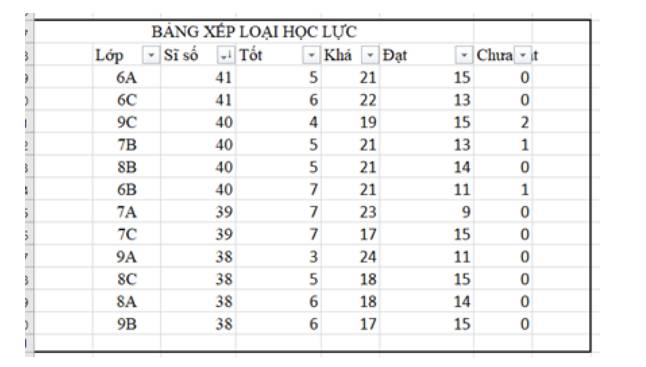
- Kết quả bảng dữ liệu được sắp xếp theo thứ tự trên một cột chính, nếu có nhiều dòng có giá trị khác nhau trên cột chính thì chúng sẽ được sắp xếp theo thứ tự trên cột phụ (khác với cột chính). Ví dụ, trong hoạt động trên, cột Sĩ số được coi là cột chính, cột Tốt là cột phụ. Do đó, cách sắp xếp số lượng học sinh xếp loại tốt của các lớp có cùng sĩ số theo thứ tự tăng dần của cột tốt.

Bài 1.6

a) \(\cos14^0=\sin76^0\)

\(\cos87^0=\sin3^0\)

Do đó: \(\cos87^0< \sin47^0< \cos14^0< \sin78^0\)

b) \(\cot25^0=\tan65^0\)

\(\cot38^0=\tan52^0\)

Do đó: \(\cot38^0< \tan62^0< \cot25^0< \tan73^0\)

Vì 8 > 7 > 3 > 1 > 0 nên -8 < -7 < -3 < -1 < 0 

Ta có: 0 < 4 < 7 < 15 < 25

Do đó: -8 < -7 < -3 < -1 < 0 < 4 < 7 < 15 < 25

Các số được sắp xếp theo thứ tự tăng dần là:  -8; -7; -3; -1; 0; +4; 7; +15; 25.

1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.

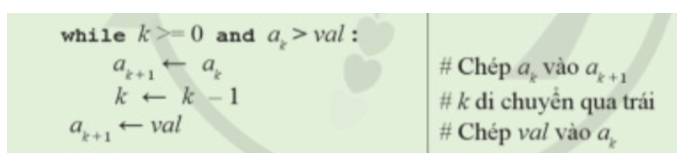
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:

Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.

Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1

Ta có: \(\frac{8}{{13}} = \frac{{80}}{{130}}\); \(0,6 = \frac{6}{{10}} = \frac{{78}}{{130}}\)

Nên \(\frac{8}{{13}} > 0,6\)

Ta có: \(\frac{{ - 5}}{6} = \frac{{ - 20}}{{24}}\); \(\frac{{ - 4}}{3} = \frac{{ - 32}}{{24}}\); \( - 1,75 = \frac{{ - 175}}{{100}} = \frac{{ - 7}}{4} = \frac{{ - 42}}{{24}}\)

Nên: \(\frac{{ - 5}}{6}\)> \(\frac{{ - 4}}{3}\)> -1,75.

=> Sắp xếp: \(\frac{8}{{13}}\); 0,6; 0; \(\frac{{ - 5}}{6}\); \(\frac{{ - 4}}{3}\); -1,75

`MSC:12`

`1/3 = (1xx4)/(3xx4)= 4/12`

`3/2=(3xx6)/(2xx6)=18/12`

`5/6=(5xx2)/(6xx2)=10/12`

`3/4=(3xx3)/(4xx3)=9/12`

`-> 4/12; 9/12; 10/12;18/12`

`->1/3; 3/4;5/6;3/2`

có `1/3=4/12`

`3/2=18/12`

`5/6=10/12`

`3/4=9/12`

vì `4<9<10<18`

`=>4/12<9/12<10/12<18/12`

`=>1/3<3/4<5/6<3/2`

`=>` sắp xếp: `1/3;3/4;5/6;3/2`