Xét dấu biểu thức sau: f(x,y)= 3x^2 + y^2 - 2x - xy + y +3

Những câu hỏi liên quan
Rút gọn cái biểu thức sau r tính giá trị biểu thức F=-(2x-y) ^3-x(2x-y)^2-y^3 tại (x-2)^2 +y^2=0 G=(x+y) (x^2-xy+y^2) +3(2x-y) (4x^2+2xy+y^2) tại x+y=2;y=-3 H=(X+3y) (x^2-3xy+9y^2) +(3x-y) (9x^2+3xy+y^2) tại 3x-y=5;x=2
a: \(F=-\left(2x-y\right)^3-x\left(2x-y\right)^2-y^3\)
\(=-\left(2x-y\right)^2\cdot\left[2x-y+x\right]-y^3\)
\(=-\left(2x-y\right)^2\cdot\left(3x-y\right)-y^3\)
\(=\left(-4x^2+4xy-y^2\right)\left(3x-y\right)-y^3\)
\(=-12x^3+4x^2y+12x^2y-4xy^2-3xy^2+y^3-y^3\)
\(=-12x^3+16x^2y-7xy^2\)
\(\left(x-2\right)^2+y^2=0\)
mà \(\left(x-2\right)^2+y^2>=0\forall x,y\)
nên dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\y=0\end{matrix}\right.\)
=>x=2 và y=0
Thay x=2 và y=0 vào F, ta được:
\(F=-12\cdot2^3+16\cdot2^2\cdot0-7\cdot2\cdot0^2\)
\(=-12\cdot2^3\)
\(=-12\cdot8=-96\)
b: \(G=\left(x+y\right)\left(x^2-xy+y^2\right)+3\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=x^3+y^3+3\left(2x-y\right)\left[\left(2x\right)^2+2x\cdot y+y^2\right]\)
\(=x^3+y^3+3\left(8x^3-y^3\right)\)
\(=x^3+y^3+24x^3-3y^3\)
\(=25x^3-2y^3\)
Ta có: \(\left\{{}\begin{matrix}x+y=2\\y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-3\\x=2-y=2-\left(-3\right)=2+3=5\end{matrix}\right.\)
Thay x=5 và y=-3 vào G, ta được:
\(G=25\cdot5^3-2\cdot\left(-3\right)^3\)
\(=25\cdot125-2\cdot\left(-27\right)\)
\(=3125+54=3179\)
c: \(H=\left(x+3y\right)\left(x^2-3xy+9y^2\right)+\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=\left(x+3y\right)\left[x^2-x\cdot3y+\left(3y\right)^2\right]+\left(3x-y\right)\left[\left(3x\right)^2+3x\cdot y+y^2\right]\)
\(=x^3+27y^3+27x^3-y^3\)
\(=28x^3-26y^3\)
Ta có: \(\left\{{}\begin{matrix}3x-y=5\\x=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3x-5=3\cdot2-5=1\end{matrix}\right.\)
Thay x=2 và y=1 vào H, ta được:
\(H=28\cdot2^3-26\cdot1^3\)
\(=28\cdot8-26\)
=198
Đúng 1
Bình luận (0)
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Phân tích mỗi đa thức sau thành nhân tử
a)x^3-2x^2y+xy^2+xy
b)x^3+4x^2y+4xy^2-9x
c)x^3-y^3+x-y
d)4x^2-4xy+2x-y+y^2
e)9x^2-3x+2y-4y^2
f)3x^2-6xy+3y^2-5x+5y
a) Xem lại đề
b) x³ - 4x²y + 4xy² - 9x
= x(x² - 4xy + 4y² - 9)
= x[(x² - 4xy + 4y² - 3²]
= x[(x - 2y)² - 3²]
= x(x - 2y - 3)(x - 2y + 3)
c) x³ - y³ + x - y
= (x³ - y³) + (x - y)
= (x - y)(x² + xy + y²) + (x - y)
= (x - y)(x² + xy + y² + 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
f) 3x² - 6xy + 3y² - 5x + 5y
= (3x² - 6xy + 3y²) - (5x - 5y)
= 3(x² - 2xy + y²) - 5(x - y)
= 3(x - y)² - 5(x - y)
= (x - y)[(3(x - y) - 5]
= (x - y)(3x - 3y - 5)
Đúng 0
Bình luận (0)
Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)
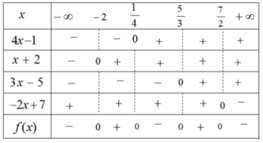
Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)
Xét dấu các biểu thức sau:
a/ y= f(x) = ( x2 + 6x - 5)(2x2 + 2x - 5)
b/y = f(x) = \(\frac{-3x^2+7x-4}{x^2-5x+6}\)
c/ y= f(x) = x3- 6x -9
d/ y= f(x) = \(\frac{x^3-6x+4}{x^2-3x+2}\)
giúp em với ạ, em cần gấp lắm ạ
Bài 1: Rút gọn các biểu thức sau
a) (5x-y)(25x mũ 2 + 5xy + y mũ 2)
b) (x-3)(x mũ 2 + 3x + 9)-(54 + x mũ 3)
c) (2x+y)(4x mũ 2 - 2xy + y mũ 2) - (2x-y)(4x mũ 2 + 2xy + y mũ 2)
d) (x+y) mũ 2 + (x-y) mũ 2 + (x+y)(x-y) - 3x mũ 2
e) (x-3) mũ 3 - (x-3)(x mũ 2 + 3x + 9) +6(x+1) mũ 2
f) (x+y)(x mũ 2 - xy + y mũ 2) + (x-y)(x mũ 2 + xy + y mũ 2) - 2x mũ 3
g) x mũ 2 + 2x(y+1) + y mũ 2 + 2y + 1
a) ( 5x - y )( 25x2 + 5xy + y2 ) = ( 5x )3 - y3 = 125x3 - y3
b) ( x - 3 )( x2 + 3x + 9 ) - ( 54 + x3 ) = x3 - 33 - 54 - x3 = -27 - 54 = -81
c) ( 2x + y )( 4x2 - 2xy + y2 ) - ( 2x - y )( 4x2 + 2xy + y2 ) = ( 2x )3 + y3 - [ ( 2x )3 - y3 ]= 8x3 + y3 - 8x3 + y3 = 2y3
d) ( x + y )2 + ( x - y )2 + ( x + y )( x - y ) - 3x2 = x2 + 2xy + y2 + x2 - 2xy + y2 + x2 - y2 - 3x2 = y2
e) ( x - 3 )3 - ( x - 3 )( x2 + 3x + 9 ) + 6( x + 1 )2
= x3 - 9x2 + 27x - 27 - ( x3 - 33 ) + 6( x2 + 2x + 1 )
= x3 - 9x2 + 27x - 27 - x3 + 27 + 6x2 + 12x + 6
= -3x2 + 39x + 6
= -3( x2 - 13x - 2 )
f) ( x + y )( x2 - xy + y2 ) + ( x - y )( x2 + xy + y2 ) - 2x3
= x3 + y3 + x3 - y3 - 2x3
= 0
g) x2 + 2x( y + 1 ) + y2 + 2y + 1
= x2 + 2x( y + 1 ) + ( y2 + 2y + 1 )
= x2 + 2x( y + 1 ) + ( y + 1 )2
= ( x + y + 1 )2
= [ ( x + y ) + 1 ]2
= ( x + y )2 + 2( x + y ) + 1
= x2 + 2xy + y2 + 2x + 2y + 1
Cho tỉ lệ thức \(\dfrac{x}{y}=\dfrac{2}{3}\). Tính giá trị của các biểu thức sau:
\(A=\dfrac{x+5y}{3x-2y}-\dfrac{2x-3y}{4x+5y}\)
\(B=\dfrac{2x^2-xy+3y^2}{3x^2+2xy+y^2}\)
Lời giải:
$\frac{x}{y}=\frac{2}{3}\Rightarrow \frac{x}{2}=\frac{y}{3}$. Đặt $\frac{x}{2}=\frac{y}{3}=k$ thì:
$x=2k; y=3k$
Khi đó: $3x-2y=3.2k-3.2k=0$. Mẫu số không thể bằng $0$ nên $A$ không xác định. Bạn xem lại.
$B=\frac{2(2k)^2-2k.3k+3(3k)^2}{3(2k)^2+2.2k.3k+(3k)^2}=\frac{29k^2}{33k^2}=\frac{29}{33}$
Đúng 2
Bình luận (0)