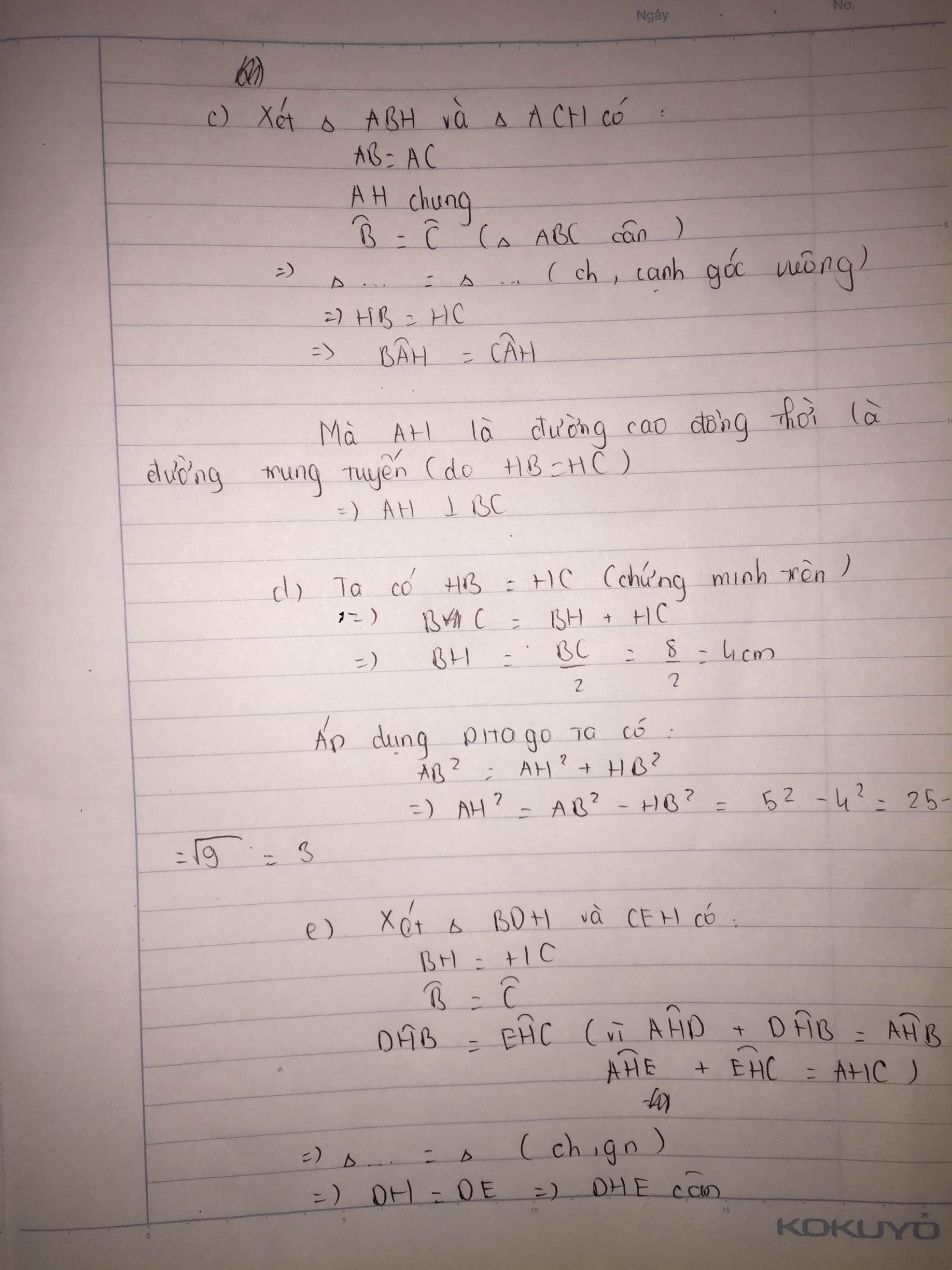Cho tam giác ABC cân có góc C= 36 độ, AB= c, AC=BC=a. Chứng minh: a^2-c^2=a*c

Những câu hỏi liên quan
Cho tam giác ABC cân tại C có góc C =36 độ , cho AB =c , AC=BC=a. Chứng minh a^2-c^2 =ac
1.Cho tam giác ABC có ABAC5cm;BC8cm.Kẻ AH vuông BC (H thuộc BC)a/ Chứng minh HBHC và góc BAHgóc CAHb/ Tính độ dài AHc/ Kẻ HD vuôngAB (D thuộc AB);HE vuông AC ( E thuộc AC ). Chứng minh rằng :Tam giác HDE cân 2.Cho tam giác ABC cân tại A ,kẻ AH vuông BC (H thuộc BC )a/ Chưng minh BAH CAHb/ Cho AH 3cm, BC 8cm .Tính độ dài ACc/ Kẻ HE vuông AB , HD vuông AC . Chứng minhAEADd/ Chứng minh ED//BC
Đọc tiếp
1.Cho tam giác ABC có AB=AC=5cm;BC=8cm.Kẻ AH vuông BC (H thuộc BC)
a/ Chứng minh HB=HC và góc BAH=góc CAH
b/ Tính độ dài AH
c/ Kẻ HD vuôngAB (D thuộc AB);HE vuông AC ( E thuộc AC ). Chứng minh rằng :Tam giác HDE cân
2.Cho tam giác ABC cân tại A ,kẻ AH vuông BC (H thuộc BC )
a/ Chưng minh BAH =CAH
b/ Cho AH = 3cm, BC = 8cm .Tính độ dài AC
c/ Kẻ HE vuông AB , HD vuông AC . Chứng minhAE=AD
d/ Chứng minh ED//BC
Xét 2 tam giác ΔAHB và ΔAHC có:
cạnh AH chung
AHB^=AHC^=90∘ (do AH ⊥ BC)
AB=AC
suy ra ΔAHB=ΔAHC (cạnh huyền- cạnh góc vuông)
⇒BH=CH và BAH^=CAH^
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A =80 độ. Trên cạnh BC lấy điểm D và E sao cho BD=CE<1\2 BC. a, Tính góc B, góc C. b, Chứg minh tam giác ADE cân
c, Kẻ DH vuông góc vs AB, EK vuông góc vs AC ( H€AB, K€ AC)
Chứng minh AH = AK.
d, Gọi M là trung điểm BC
Chứng minh AM,DH,EK cắt nhau tại 1điểm
a) tam giác abc có a+b+c=180'
hay 80+b+c=180
b+c=100
mà b=c(tam giác abc cân tại a)
=> b=c=50
b)Xét tam giác abd và aec có
ab=ac(gt)
góc b=góc c(gt)
bd=ec(gt)
do đó,abd=ace (c-g-c)
=> ad=ae (2 cạnh tương ứng)
=>tam giác ade cân tại a
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A kẻ AH vuông góc với BC(H thuộc BC)
a, Chứng minh: tam giác AHC= tam giác AHC
b, Kẻ HD vuông góc với AB(D thuộc AB), HE vuông góc với AC(E thuộc AC): Chứng minh tam giác HDE Cân
c,Nếu cho góc A=120 độ thì tam giác HDE trở thành tam giác gì? Vì sao?
Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 6cm. Phân giác góc B cắt AC tại M, phân giác góc C cắt AB tại N : a) Chứng minh MN // BC b) Tính độ dài AM ? MC ? MN ? c) Tính SAMN ?
cho tam giác abc có góc a bằng 90 độ ab bằng ac gọi k là trung điểm của bc a chứng minh tam giác akb bằng tam giác ac b chứng minh ak vuông góc với bc c từ c vẽ đường vuông góc với bc tại c cắt đường thẳng ab tại a chứng minh ac // ak
Câu 5: Cho tam giác ABC cân tại A, có AB = AC = 5 cm, BC = 8 cm. AH là phân giác của góc A ( H nằm trên cạnh BC).
(Ko cần gửi hình vẽ đâu ạ!)
c. Chứng minh AH ⊥ BC
d. Tính độ dài AH
e. Kẻ HD⊥AB(D ∈ AB ; HE⊥AC (E∈AC). Chứng minh tam giác HDE là tam giác cân.
Giúp em nhanh với ạ, e c.ơn :<
c, Xét tam giác ABC cân tại A có AH là đường phân giác
nên AH đồng thời là đường cao, là đường trung tuyến
=> AH vuông BC
d, Vì AH là trung tuyến => BH = BC/2 = 4 cm
Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH^2}=\sqrt{5^2-4^2}=3cm\)
e, Xét tam giác ADH và tam giác AEH có :
^ADH = ^AEH = 900
AH _ chung
DAH = ^EAH ( AH là đường phân giác )
Vậy tam giác ADH = tam giác AEH ( ch - gn )
=> HD = HE
Xét tam giác HDE có HD = HE
Vậy tam giác HDE cân tại H
Đúng 1
Bình luận (0)
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{c+a}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{c+a}+\dfrac{bc}{a+b}\). Chứng minh: Tam giác ABC cân
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{a+c}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{a+c}+\dfrac{bc}{a+b}\). Chứng minh tam giác ABC cân
\(\Leftrightarrow ab\left(\dfrac{1}{b+c}-\dfrac{1}{a+c}\right)+bc\left(\dfrac{1}{a+c}-\dfrac{1}{a+b}\right)+ca\left(\dfrac{1}{a+b}-\dfrac{1}{b+c}\right)=0\)
\(\Leftrightarrow\dfrac{ab\left(a-b\right)}{\left(b+c\right)\left(a+c\right)}+\dfrac{bc\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{ca\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}=0\)
\(\Leftrightarrow\dfrac{ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)\left(a+b+c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\) hay tam giác cân
Đúng 1
Bình luận (0)