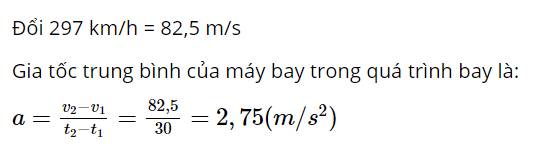Một máy bay chở khách đạt tốc độ cất cánh là 297 km/h ở cuối đoạn đường băng sau 30 giây từ lúc bắt đầu lăn bánh. Giả sử máy bay chuyển động thẳng, hãy tính gia tốc trung bình của máy bay trong quá trình này.

Những câu hỏi liên quan
1. Một máy bay chở khách đạt tốc độ cất cánh là 297 km/h ở cuối đoạn đường băng sau 30 giây từ lúc bắt đầu lăn bánh. Giả sử máy bay chuyển động thẳng, hãy tính gia tốc trung bình của máy bay trong quá trình này.
Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc \({20^ \circ }\) và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).
Đổi \(200km/h = \frac{{500}}{9}m/s\)
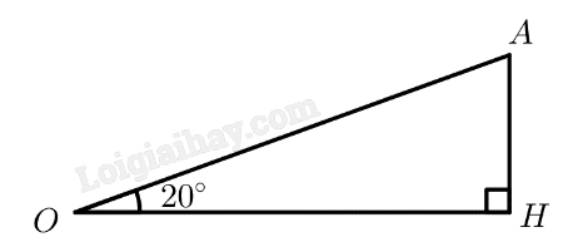
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.
Đúng 0
Bình luận (0)
2. Một máy bay chở khách có khối lượng tổng cộng là 300 tấn. Lực đẩy tối đa của động cơ là 440 kN. Máy bay phải đạt tốc độ 285 km/h mới có thể cất cánh. Hãy tính chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được, bỏ qua ma sát giữa bánh xe của máy bay và mặt đường băng và lực cản không khí.
Một máy bay chở khách có khối lượng tổng cộng là 300 tấn. Lực đẩy tối đa của động cơ là 440 kN. Máy bay phải đạt tốc độ 285 km/h mới có thể cất cánh. Hãy tính chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được, bỏ qua ma sát giữa bánh xe của máy bay và mặt đường băng và lực cản không khí.
Ta có m = 300 tấn = 3.105 kg; F = 440 kN = 4,4.105 N; v = 285 km/h = 475/6 m/s
Gia tốc của máy bay là: \(a = \frac{F}{m} = \frac{{4,{{4.10}^5}}}{{{{3.10}^5}}} = \frac{{22}}{{15}}(m/{s^2})\)
Chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được là:
\(s = \frac{{{v^2} - v_0^2}}{{2.a}} = \frac{{{{\left( {\frac{{475}}{6}} \right)}^2}}}{{2.\frac{{22}}{{15}}}} \approx 2136,6(m)\)
Đúng 1
Bình luận (0)
Một máy bay bắt đầu chuyển động nhanh dần đều trên một đường băng dài với gia tốc 5m / s . Sau khi chạy được quãng đường băng dài 1km thì cất cánh . Hỏi vận tốc lúc cất cánh là bao nhiêu ?
Câu 1: Một máy bay Boeing 747 có khối lượng 500 tấn, để có thể cất cánh vận tốc của máy bay phải đạt đến 250 km/h. Giả sử đường băng dài 4km, hỏi lực phát động của máy bay phải đạt tối thiểu là bao nhiêu?
Đọc tiếp
Câu 1: Một máy bay Boeing 747 có khối lượng 500 tấn, để có thể cất cánh vận tốc của máy bay phải đạt đến 250 km/h. Giả sử đường băng dài 4km, hỏi lực phát động của máy bay phải đạt tối thiểu là bao nhiêu?
Vật bắt đầu cất cánh có \(v_0=0\).
\(v=250km/h=\dfrac{625}{9}m/s\)
Gia tốc vật: \(a=\dfrac{v^2-v_0^2}{2S}=\dfrac{\left(\dfrac{625}{9}\right)^2-0}{2\cdot4000}=0,6m/s^2\)
Lực phát động của máy bay:
\(F=m\cdot a=500\cdot1000\cdot0,6=3\cdot10^5N\)
Đúng 1
Bình luận (0)
Một chiếc máy bay chuyển động trên đường băng với vận tốc
v
t
t
2
+
10
t
(m/s) với t là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. BIết khi máy bay đạt vận tốc 200 (m/s) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là A. 500 (m) B. 2000 (m) C.
2500
3
(m) D. ...
Đọc tiếp
Một chiếc máy bay chuyển động trên đường băng với vận tốc v t = t 2 + 10 t (m/s) với t là thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. BIết khi máy bay đạt vận tốc 200 (m/s) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là
A. 500 (m)
B. 2000 (m)
C. 2500 3 (m)
D. 4000 3 (m)
Một chiếc máy bay đang bay song song với mặt đất ở độ cao 18km thì bắt đầu hạ cánh, đường đi của máy bay tạo 1 góc 30 độ so với mặt đất. Sau khi tiếp đất, máy bay đi thẳng với vận tốc trung bình là 24km/h để đến điểm trả khách. Hỏi hành khách phải chờ bao nhiêu phút để tới điểm trả khách tính từ lúc máy bay tiếp đất, biết quãng đường từ điểm bắt đầu hạ cánh đến điểm trả khách là 44,8km ?CẦN GẤP ạ
Đọc tiếp
Một chiếc máy bay đang bay song song với mặt đất ở độ cao 18km thì bắt đầu hạ cánh, đường đi của máy bay tạo 1 góc 30 độ so với mặt đất. Sau khi tiếp đất, máy bay đi thẳng với vận tốc trung bình là 24km/h để đến điểm trả khách. Hỏi hành khách phải chờ bao nhiêu phút để tới điểm trả khách tính từ lúc máy bay tiếp đất, biết quãng đường từ điểm bắt đầu hạ cánh đến điểm trả khách là 44,8km ?
CẦN GẤP ạ
Để cất cánh trên đường băng dài 100m của một tàu sân bay thì máy bay phản lực phải tăng tốc từ 0km/h đến 198km/h khi ở cuối đường băng.hãy tính:
a) Gia tốc của máy bay khi đó
b) Thời gian máy bay tăng tốc
a) Đổi 198km/h = 55m/s
Gia tốc của máy bay:
Ta có: \(v^2-v^2_0=2as\Leftrightarrow a=\dfrac{v^2-v^2_0}{2s}=\dfrac{55^2-0^2}{2.100}=15,125\left(m/s^2\right)\)
b) Thời gian máy bay tăng tốc:
Ta có: \(v=v_0+at\Leftrightarrow t=\dfrac{v-v_0}{a}=\dfrac{55-0}{15,125}=\dfrac{40}{11}\left(s\right)=3,6363\left(s\right)\)
Đúng 2
Bình luận (0)