$10'=\dfrac{1}{6}h$

Gọi $x(km)$ là độ dài quãng đường AB $(x>0)$

Thời gian ô tô dự định đi là: $\dfrac{x}{48}(h)$

Quãng đường đi trong 1h với vận tốc $48km/h$ là: $48.1=48(km)$

Vận tốc tăng lên là: $48+6=54(km/h)$

Độ dài quãng đường là: $x-48(km)$

Thời gian đi là: $\dfrac{x-48}{54}(h)$

Theo đề bài, ta có phương trình:

$\dfrac{x}{48}=1+\dfrac{x-48}{54}+\dfrac{1}{6}$

$⇔\dfrac{9x}{432}=\dfrac{432}{432}+\dfrac{8(x-48)}{432}+\dfrac{72}{432}$

$⇔9x=432+8x-384+72$

$⇔x=120 \text{(nhận)}$

Vậy quãng đường AB dài $120km$

Đáp án C

* Phân tích:

Ta luôn có: Quãng đường = vận tốc . thời gian

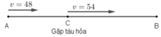
Gọi C là địa điểm ô tô gặp tàu hỏa.

Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.

Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).

Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).

	Quãng đường BC	Vận tốc	Thời gian
Dự tính	x	48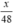
Thực tế	x	48 + 6 = 54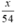

Ta có phương trình: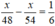 

* Giải:

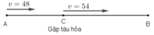
Gọi C là địa điểm ô tô gặp tàu hỏa.

Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ

⇒ SAC = 48.1 = 48 (km).

Gọi quãng đường BC dài là x (km; x > 0).

Vận tốc dự tính đi trên BC là: 48 km/h

⇒ Thời gian dự tính đi quãng đường BC hết: 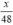 (giờ).

Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).

⇒ Thời gian thực tế ô tô đi quãng đường BC là: 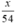 (giờ).

Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).

Do đó ta có phương trình:

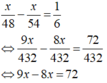
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).

Vậy quãng đường AB là:

SAB = SAC + SBC = 48 + 72 = 120 (km).

* Phân tích:

Ta luôn có: Quãng đường = vận tốc . thời gian

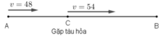
Gọi C là địa điểm ô tô gặp tàu hỏa.

Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.

Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).

Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).

	Quãng đường BC	Vận tốc	Thời gian
Dự tính	x	48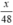
Thực tế	x	48 + 6 = 54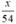

Ta có phương trình: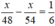 

* Giải:

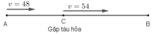
Gọi C là địa điểm ô tô gặp tàu hỏa.

Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ

⇒ SAC = 48.1 = 48 (km).

Gọi quãng đường BC dài là x (km; x > 0).

Vận tốc dự tính đi trên BC là: 48 km/h

⇒ Thời gian dự tính đi quãng đường BC hết: 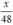 (giờ).

Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).

⇒ Thời gian thực tế ô tô đi quãng đường BC là: 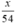 (giờ).

Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).

Do đó ta có phương trình:

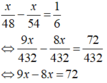
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).

Vậy quãng đường AB là:

SAB = SAC + SBC = 48 + 72 = 120 (km).

Đổi 10 p = \(\dfrac{1}{6}h\)

Gọi x (km) là độ dài quãng đường AB (x > 0)

Đoạn đường đi trong 1 h đầu là 48 km

Đoạn đường còn lại là x - 48 (km)

Thời gian dự định đi từ điểm bị tàu hỏa chắn đường đến B là: \(t_1=\dfrac{x-48}{48}\) (h)

Thời gian thực tê đi từ điểm bị tàu hỏa chắn đường đến B là \(t_2=\dfrac{x-48}{48+6}=\dfrac{x-48}{54}\) (h)

Vì ô tô bị tàu hỏa chắn đường trong 10p nên:

\(\dfrac{x-48}{48}-\dfrac{x-48}{54}=\dfrac{1}{6}\) (1)

Giải PT (1) <=> x = 120 (t/m ĐK)

Vậy quảng đường AB dài 120

P/s: Ko chắc nha

Bài 1:

Đổi 10 phút thành 1/6 giờ

Thời gian đi dự định: $\frac{AB}{48}$ (h)

Thời gian đi thực tế: $1+\frac{1}{6}+\frac{AB-48}{48+6}$

$=\frac{7}{6}+\frac{AB-48}{54}$ (h)

Ta có: $\frac{AB}{48}=\frac{7}{6}+\frac{AB-48}{54}$
$\Leftrightarrow \frac{AB}{432}=\frac{5}{18}$

$\Rightarrow AB=120$ (km)

Bài 2: 

Đổi 1h40 phút thành $\frac{5}{3}$ giờ, đổi 20 phút thành $\frac{1}{3}$ giờ

Thời gian dự định đi: $\frac{AB}{12}$ (giờ)

Thời gian thực tế: \(\frac{AB}{3.12}+\frac{1}{3}+\frac{2AB}{3.36}=\frac{5AB}{108}+\frac{1}{3}\) (giờ)

Theo bài ra:

$\frac{5AB}{108}+\frac{1}{3}+\frac{5}{3}=\frac{AB}{12}$

$\Leftrightarrow AB=54$ (km)

Bài 3:

Đổi 30 phút thành 1/2 giờ

Thời gian dự định: $\frac{AB}{50}$ (giờ)

Thời gian thực tế: \(\frac{AB}{3.50}+\frac{2AB}{3(50-10)}=\frac{7AB}{300}\) (giờ)

Theo bài ra ta có:

\(\frac{7AB}{300}-\frac{1}{2}=\frac{AB}{50}\Rightarrow AB=150 \) (km)

48*2.5=120 km

11111111111111111111111111111111111111111111111111111111111111111111111111111111111

Giống câu hỏi của mk nhưng mk k bt làm ahiuhiu. Ban nào giúp mk vs

Mình trình bày nè!
Gọi t là thời gian người đó đi từ A đến B
Ta có phương trình:
48t= 48+54(t-1-1/6)
Từ phương trình trên bạn sẽ tính được thời gian là 2.5(h). 
Từ đó bạn sẽ dễ dàng tính được quãng đường AB bằng 120km

:3

Gọi độ dài quãng đường AB là x

Thời gian dự kiến là x/48

Thời gian thực tế là 7/6+(x-48)/54

Theo đề, ta có: \(\dfrac{x-48}{54}+\dfrac{7}{6}=\dfrac{x}{48}\)

=>8(x-48)+7*72=9x

=>8x-384+504-9x=0

=>x=120