(2023 + 437) + [- 137 + (- 2023)]
giúp mình với
Tìm x biết: (x – 2023)22 − ( x – 2023) = 0 Giúp mình với mình đang cần gấp
=>(x-2023)[(x-2023)^21-1]=0
=>x-2023=0 hoặc x-2023=1
=>x=2023 hoặc x=2024
So sánh:
B=2020/2021+2021/2022+2022/2023+2023/2020 và 4
Giải chi tiết giúp minh với ạ
Mai mình phải nộp rồi
2020/2021<1
2021/2022<1
2022/2023<1
2023/2020=1+1/2020+1/2020+1/2020>1+1/2021+1/2022+1/2023
=>B>2020/2021+2021/2022+2022/2023+1/2021+1/2022+1/2023+1=4
Giúp mình câu nâng cao này với: 5x²+2y²+6xy-8x-4y+4=0. Tính giá trị biểu thức P=x^2023+y^2023
\(5x^2+2y^2+6xy-8x-4y+4=0\)
\(\Leftrightarrow4x^2+x^2+y^2+y^2+2xy+4xy-8x-4y+4=0\)
\(\Leftrightarrow\left(4x^2+y^2+4+4xy-8x-4y\right)+\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow\left[\left(2x\right)^2+4xy+y^2-4\left(2x+y\right)+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left[\left(2x+y\right)^2-2\cdot\left(2x+y\right)\cdot2+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Ta có: \(\left\{{}\begin{matrix}\left(2x+y-2\right)^2\ge0\forall x,y\\\left(x+y\right)^2\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2\ge0\forall x,y\)
Mặt khác: \(\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}2x+y-2=0\\x+y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(-y\right)+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2y+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=2\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=2\end{matrix}\right.\)
Thay x,y vào P ta có:
\(P=2^{2023}+\left(-2\right)^{2023}=2^{2023}-2^{2023}=0\)
Vậy: ...
cho( x-1)^2022+/y+1/=0 tính giá trị biểu thức p=x^2023.y^2022/(2x+y)^2022+2023
ai giúp mình với
olm sẽ hướng dẫn em làm bài này như sau:
Bước 1: em giải phương trình tìm; \(x\); y
Bước 2: thay\(x;y\) vào P
(\(x-1\))2022 + |y + 1| = 0
Vì (\(x-1\))2022 ≥ 0 ∀ \(x\); |y + 1| ≥ 0 ∀ y
⇒ (\(x\) - 1)2022 + |y + 1| = 0
⇔ \(\left\{{}\begin{matrix}\left(x-1\right)^{2022}=0\\y+1=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\) (1)
Thay (1) vào P ta có:
12023.(-1)2022 : )(2.1- 1)2022 + 2023
= 1 + 2023
= 2024
mọi người hãy trình bầy rõ ra nhé
em ko hiểu nên nếu nói tắt sẽ ko thể tiếp thu
Giúp mình với!!!
So sánh A=\(\dfrac{2024^{2023}+1}{2024^{2024}+1}\) và B=\(\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
Cám ơn các bạn!
\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)
c, C = 2020/1.2 + 2020/2.3 + 2020/3.4 + ... + 2020/2019.2020
d, D = 2020/1.3 + 2020/3.5 + 2020/5.7 + ... + 2020/2019.2021
e, E = 2023/ 1.3 + 2023/3.5 + 2023/5.7 + ... + 2023/2019.2020
f, F = 1/15 + 1/35 + 1/63 + ... + 1/657
giúp với mình cần gấp lắm
giúp mình với !!!!!!!!!!!!!!!!!!! đang cần gấp !!!!!!!!!!!!!!!
cho biểu thức a= 6+ 5\(^2\) + 5\(^3\) +........+ 5\(^{2022}\) + 5\(^{2023}\) . chứng minh 4a + 1 chia hết cho 5\(^{2023}\)
Lời giải:
$a=1+5+5^2+5^3+...+5^{2022}+5^{2023}$
$5a=5+5^2+5^3+5^4+....+5^{2023}+5^{2024}$
$\Rightarrow 5a-a=5^{2024}-1$
$\Rightarrow 4a=5^{2024}-1$
$\Rightarrow 4a+1=5^{2024}\vdots 5^{2023}$ (đpcm)
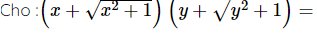 2023
2023 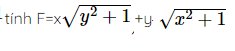 ai giúp với ạ mình cần gấp
ai giúp với ạ mình cần gấp