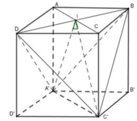
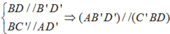Cho hình hộp ABCD.A'B'C'D' mặt phẳng (C'BD) song song với mặt phẳng nào
Những câu hỏi liên quan
Cho hình hộp
A
B
C
D
.
A
B
C
D
, và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là : A. Hình ngũ giác B. Hình lục giác C. Hình tam giác D. Hình tứ giác
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' , và một điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Cắt hình hộp bởi mặt phẳng (P) thì thiết diện là :
A. Hình ngũ giác
B. Hình lục giác
C. Hình tam giác
D. Hình tứ giác
Cho hình hộp chữ nhật ABCD.ABCD có mặt ABCD là hình vuông,
A
A
A
B
6
2
. Xác định góc giữa hai mặt phẳng (ABD) và (CBD)
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có mặt ABCD là hình vuông, A A ' = A B 6 2 . Xác định góc giữa hai mặt phẳng (A'BD) và (C'BD)
7 tháng 4 2023 lúc 19:22
1Cho hình hộp chữ nhật ABCD.ABCD (h.71)a) Những cạnh nào của hình hộp bằng cạnh AB? Vì sao?b) Đường thẳng CD có song song với đường thẳng CD không? Vì sao?c) Đường thẳng AD song song với những mặt phẳng nào? Vì sao?d) Em hãy chỉ ra một mặt phẳng song song với mặt phẳng (ADDA)2: Trang 89 sách VNEN 8 tập 2 Cho hình hộp chữ nhật ABCD.ABCD (h.71)a) Em hãy chỉ ra hai mặt phẳng chứa đường thẳng BCb) Em hãy chỉ ra bốn đường thẳng có điểm chung với đường thẳng CDc) Em hãy chỉ ra đường thẳng chung của ha...
Đọc tiếp
1
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Những cạnh nào của hình hộp bằng cạnh AB? Vì sao?
b) Đường thẳng C'D' có song song với đường thẳng CD không? Vì sao?
c) Đường thẳng AD song song với những mặt phẳng nào? Vì sao?
d) Em hãy chỉ ra một mặt phẳng song song với mặt phẳng (ADD'A')
2: Trang 89 sách VNEN 8 tập 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Em hãy chỉ ra hai mặt phẳng chứa đường thẳng BC
b) Em hãy chỉ ra bốn đường thẳng có điểm chung với đường thẳng C'D'
c) Em hãy chỉ ra đường thẳng chung của hai mặt phẳng (ADD'A') và (CDD'C')
3: Trang 89 sách VNEN 8 tập 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Hai đường thẳng AB và C'D' có song song với nhau không? Vì sao?
b) Hai đường thẳng AD và B'C' có song song với nhau không? Vì sao?
c) Hai đường thẳng AA' và CC' có song song với nhau không? Vì sao?
3:
a: AB//CD
CD//C'D'
=>AB//C'D'
b: AD//BC
CB//B'C'
=>AD//B'C'
c: AA'//D'D
D'D//CC'
=>AA'//CC'
Đúng 0
Bình luận (0)
7 tháng 4 2023 lúc 19:59
1Cho hình hộp chữ nhật ABCD.ABCD (h.71)a) Những cạnh nào của hình hộp bằng cạnh AB? Vì sao?b) Đường thẳng CD có song song với đường thẳng CD không? Vì sao?c) Đường thẳng AD song song với những mặt phẳng nào? Vì sao?d) Em hãy chỉ ra một mặt phẳng song song với mặt phẳng (ADDA)2Cho hình hộp chữ nhật ABCD.ABCD (h.71)a) Em hãy chỉ ra hai mặt phẳng chứa đường thẳng BCb) Em hãy chỉ ra bốn đường thẳng có điểm chung với đường thẳng CDc) Em hãy chỉ ra đường thẳng chung của hai mặt phẳng (ADDA) và (CDDC)3...
Đọc tiếp
1
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Những cạnh nào của hình hộp bằng cạnh AB? Vì sao?
b) Đường thẳng C'D' có song song với đường thẳng CD không? Vì sao?
c) Đường thẳng AD song song với những mặt phẳng nào? Vì sao?
d) Em hãy chỉ ra một mặt phẳng song song với mặt phẳng (ADD'A')
2
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Em hãy chỉ ra hai mặt phẳng chứa đường thẳng BC
b) Em hãy chỉ ra bốn đường thẳng có điểm chung với đường thẳng C'D'
c) Em hãy chỉ ra đường thẳng chung của hai mặt phẳng (ADD'A') và (CDD'C')
3
Cho hình hộp chữ nhật ABCD.A'B'C'D' (h.71)
a) Hai đường thẳng AB và C'D' có song song với nhau không? Vì sao?
b) Hai đường thẳng AD và B'C' có song song với nhau không? Vì sao?
c) Hai đường thẳng AA' và CC' có song song với nhau không? Vì sao?
1:
a: AB=CD=A'B'=C'D'
b: C'D'//CD vì CDD'C là hình bình hành
c: AD//(B'BCC')
AD//(A'B'C'D')
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A'B'C'D'. Trên cạnh AB lấy điểm M khác A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (ACD').
a) Trình bày cách dựng thiết diện của hình hộp và mặt phẳng (P)
b) Xác định vị trí của M để thiết diện nói trên có diện tích lớn nhất
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng nào sau đây?
A. (BA’C’).
B. (C’BD).
C. (BDA’).
D. (ACD’).
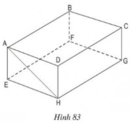
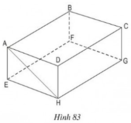
Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH). a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH). b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật? c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
Đọc tiếp
Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH).
a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH).
b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?
c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
Đúng 0
Bình luận (0)
Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH).a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH).b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
Đọc tiếp
Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH).
a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH).
b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?
c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
Đúng 0
Bình luận (0)
Giải mục 1 trang 113, 114 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 21:05
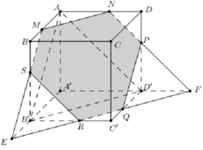
Cho hình hộp \(ABCD.A'B'C'D'\) và một mặt phẳng \(\left( \alpha \right)\) cắt các mặt của hình hộp theo các giao tuyến \(MN,NP,PQ{\rm{,}}QR,RS,SM\) như Hình 18. Chứng minh các cặp cạnh đối của lục giác \(MNPQRS\) song song với nhau.
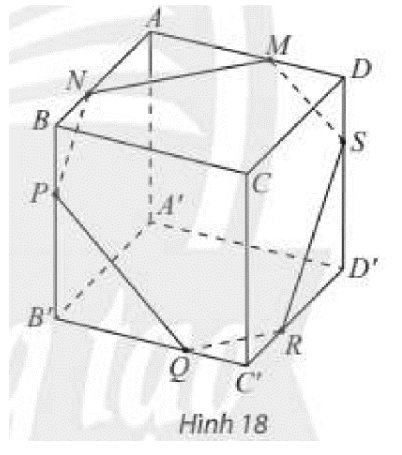
Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)
Đúng 0
Bình luận (0)