(x;y)=(0;0);(2;2)

Tình cảm gia đình là một nguồn cảm hứng bất tận đối với các thi sĩ, đã có rất nhiều tác phẩm làm xúc động lòng người về đề tài thiêng liêng này. Bài thơ Bếp lửa của tác giả cũng viết về đề tài này, thắp sáng tình cảm bà cháu. Đặc biệt là qua ba câu thơ:“ Rồi sớm, rồi chiều lại bếp lửa bà nhemMột ngọn lửa lòng bà luôn ủ sẵnMột ngọn lửa luôn chứa niềm tin dai dẳng…”Ta thấy qua những vần thơ giản dị, từng từ, chữ của tác giả-người cháu xa nhà, đãgợi ra sự hi sinh tần tảo của bà. Ba câu thơ như một nốt nhấn, một điệp khúc khó quên trong bản tình ca về bà cháu đầy thiêng liêng mà cao quý. Hình ảnh ngọn lửa tỏa sáng trong câu thơ có sức truyền lan tỏa, có một sự truyền cảm mạnh mẽ. giữa những mất mát đau thương, bà vẫn là người ngày ngày nhóm bếp lửa chất chứa bao nét đẹp ý nghĩa, sự tinh tế, bình dị, đơn sơ và tình yêu thương của bà với cháu. “Rồi sớm, rồi chiều” bà vẫn nhóm lên ngọn lửa như nhóm trong lên trong người cháu một tình cảm rộng lớn ấp ủ bằng tình thương bao la dạt dào suốt cuộc đời bà dành cho cháu. Bếp lửa của tình thương gia đình, quê hương giờ đây đã trở thành một “ngọn lửa” mang đậm giá trị biểu tượng. lời thơ thủ thỉ, dịu êm mà sao tiếng lòng của người thi sĩ như có sức mạnh thần kì làm cho người đọc thấy con tim mình như có lửa bùng lên. “Một ngọn lửa” luôn luôn có sẵn trong lòng bà, luôn ấp ủ, lo toan. “Một ngọn lửa’ chứa niềm tin cháy rực trong lòng cháu mang theo bao cảm xúc không thể nói hết mà phải dùng dấu chấm lửng để lại bao suy tư trong lòng người đọc. Bà đã để lại cho cháu không phải là một giá trị vật chất thông thường mà là một điều vô cùng quý giá. Hình ảnh người bà giờ đây thật là cao quý,bà hiện thân cho vẻ đẹp thiêng liêng của người giữ lửa người truyền lửa muôn đời

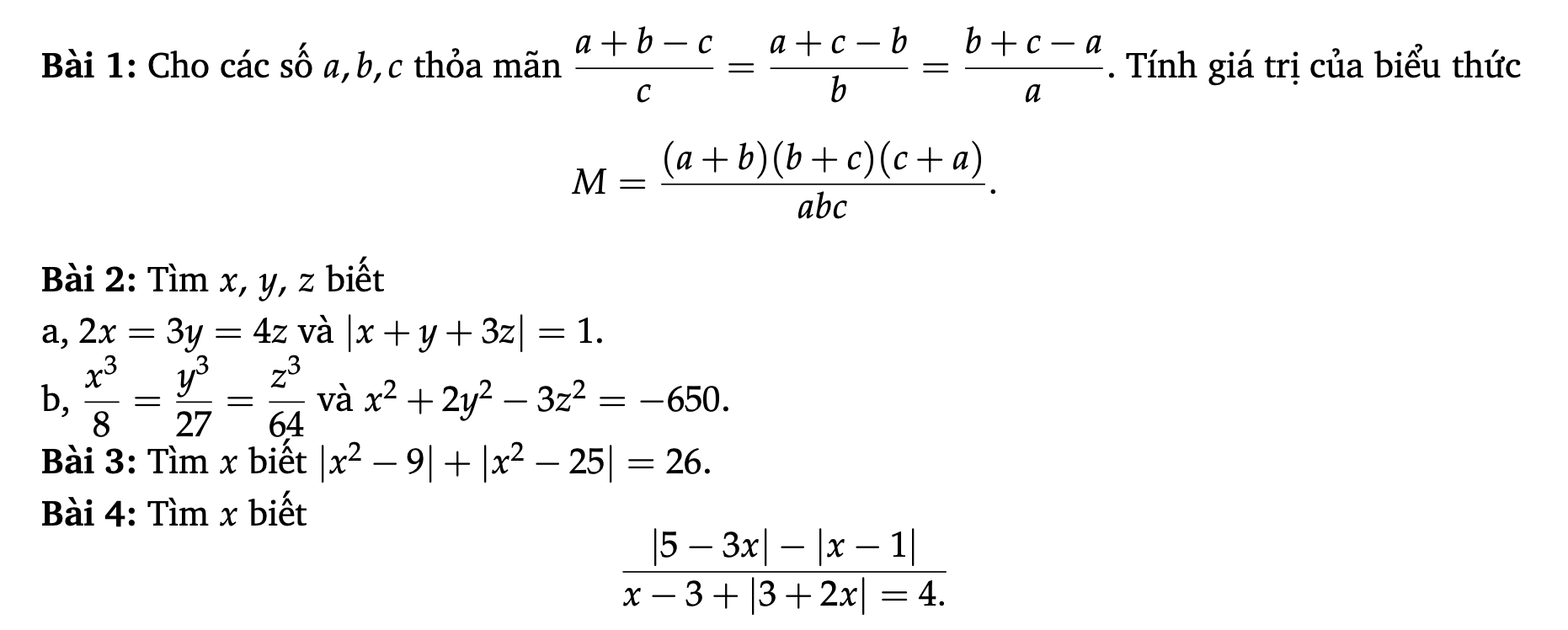
1, \(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)

 =>   \(\dfrac{a+b}{c}-1=\dfrac{a+c}{b}-1=\dfrac{b+c}{a}-1\)

 =>   \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}\)

=>    \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}=\dfrac{a+b+a+c+b+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)

=>  \(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{a+b}{c}\times\dfrac{a+c}{b}\times\dfrac{b+c}{a}=2.2.2=8\)

=>   \(M=8\)

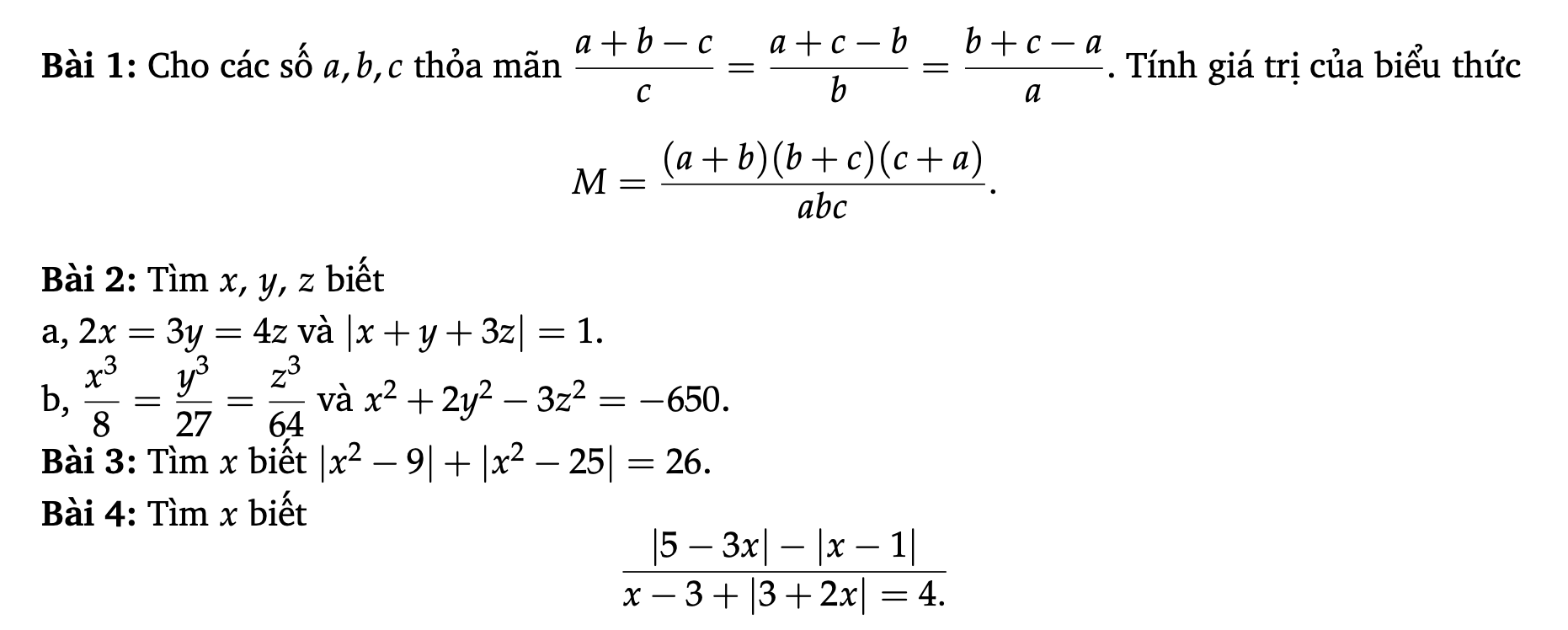
Bài 1:

Nếu $a+b+c=0$ thì đkđb thỏa mãn

$M=\frac{(-c)(-a)(-b)}{abc}=\frac{-(abc)}{abc}=-1$

Nếu $a+b+c\neq 0$. Áp dụng TCDTSBN:

$\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{c+b+a}=\frac{a+b+c}{a+b+c}=1$

$\Rightarrow a+b-c=c; a+c-b=b; b+c-a=a$

$\Leftrightarrow a+b=2c; a+c=2b; b+c=2a$

$\Rightarrow a=b=c$

$M=\frac{(a+a)(a+a)(a+a)}{aaa}=\frac{8a^3}{a^3}=8$

Bài 2a

Đặt $2x=3y=4z=t$

$\Rightarrow x=\frac{t}{2}; y=\frac{t}{3}; z=\frac{t}{4}$

Khi đó:

$|x+y+3z|=1$

$\Leftrightarrow |\frac{t}{2}+\frac{t}{3}+\frac{3t}{4}|=1$

$\Leftrightarrow |\frac{19}{12}t|=1$

$\Rightarrow t=\pm \frac{12}{19}$

Nếu $t=\frac{12}{19}$ thì:

$x=\frac{t}{2}=\frac{6}{19}; y=\frac{4}{19}; z=\frac{3}{19}$

Nếu $t=-\frac{12}{19}$ thì:

$x=\frac{t}{2}=\frac{-6}{19}; y=\frac{-4}{19}; z=\frac{-3}{19}$

Bài 2b:

$\frac{x^3}{8}=\frac{y^3}{27}=\frac{z^3}{64}$

$\Leftrightarrow (\frac{x}{2})^3=(\frac{y}{3})^3=(\frac{z}{4})^3$

$\Leftrightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$

Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$

$\Rightarrow x=2t; y=3t; z=4t$

Khi đó:
$x^2+2y^2-3z^2=-650$

$\Leftrightarrow (2t)^2+2.(3t)^2-3(4t)^2=-650$

$\Leftrightarrow -26t^2=-650$

$\Leftrightarrow t=\pm 5$

Nếu $t=5$ thì:

$x=2t=10; y=3t=15; z=4t=20$

Nếu $t=-5$ thì:

$x=2t=-10; y=3t=-15; z=4t=-20$

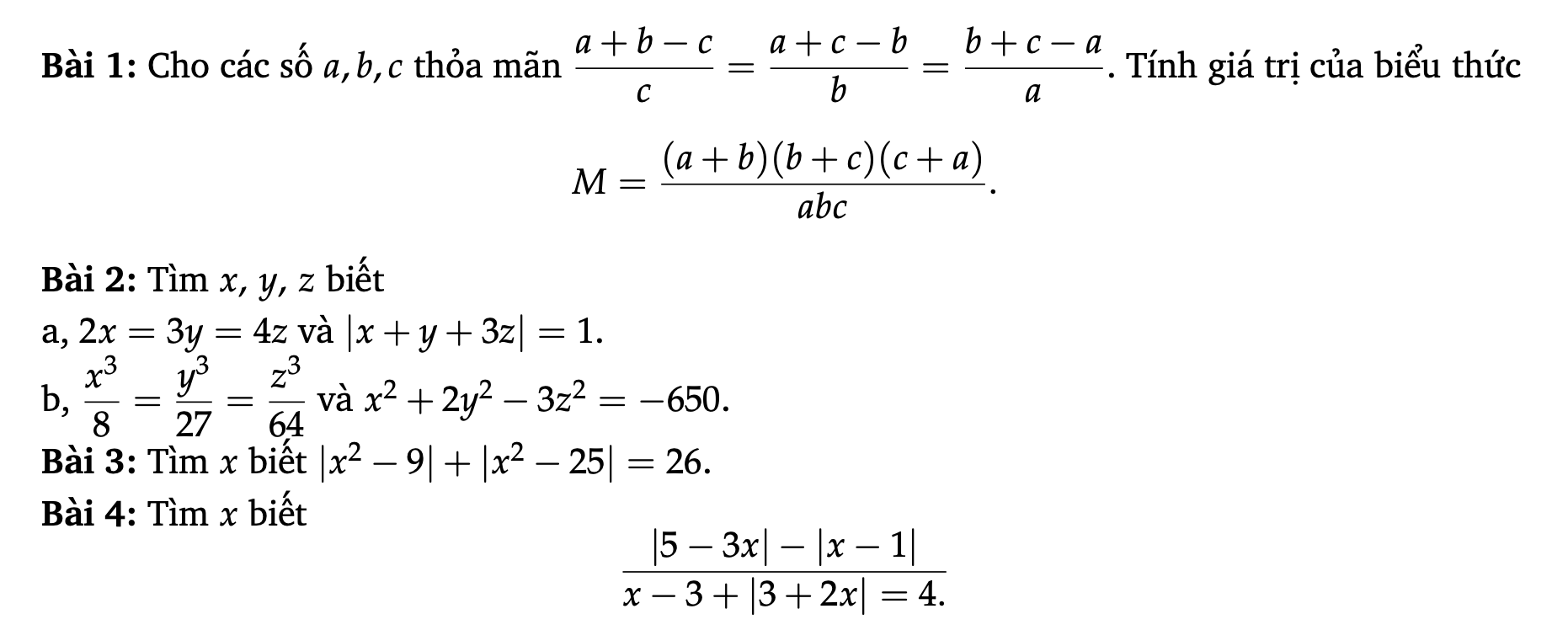
Bài 1:

Với \(a+b+c=0\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\c+a=-b\end{matrix}\right.\Leftrightarrow M=\dfrac{-abc}{abc}=-1\)

Với \(a+b+c\ne0\Leftrightarrow\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}=\dfrac{a+b+c}{a+b+c}=1\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b-c=c\\a+c-b=b\\b+c-a=a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=2c\\b+c=2a\\c+a=2b\end{matrix}\right.\Leftrightarrow M=\dfrac{2a\cdot2b\cdot2c}{abc}=8\)

Bài 2:

\(a,TH_1:x+y+3z=1\\ \Leftrightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+3z}{6+4+9}=\dfrac{1}{19}\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6}{19}\\y=\dfrac{4}{19}\\z=\dfrac{3}{19}\end{matrix}\right.\\ TH_2:x+y+3z=-1\\ \Leftrightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+3z}{6+4+9}=\dfrac{-1}{19}\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{6}{19}\\y=-\dfrac{4}{19}\\z=-\dfrac{3}{19}\end{matrix}\right.\)

Bài 2:

\(b,\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Leftrightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{16}=\dfrac{x^2+2y^2-3z^2}{4+18-48}=\dfrac{-650}{-26}=25\\ \Leftrightarrow\left\{{}\begin{matrix}x^2=100\\y^2=225\\z^2=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=15\\z=20\end{matrix}\right.\)

 

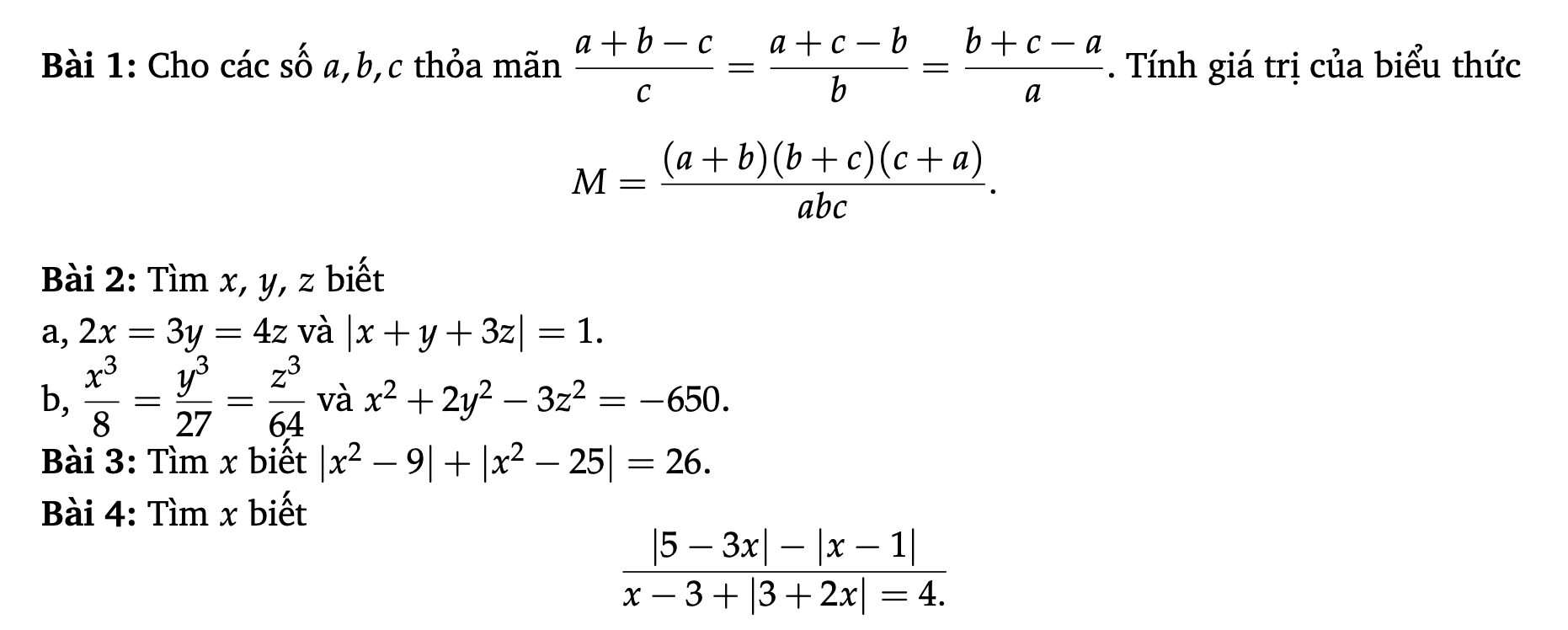
1. TH1:a+b+c≠0

Áp dụng t/c dtsbn ta có:

\(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}=\dfrac{a+b-c+a+c-b+b+c-a}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)

\(\dfrac{a+b-c}{c}=1\Rightarrow a+b-c=c\Rightarrow a+b=2c\\ \dfrac{a+c-b}{b}=1\Rightarrow a+c-b=b\Rightarrow a+c=2b\\ \dfrac{b+c-a}{a}=1\Rightarrow b+c-a=a\Rightarrow b+c=2a\)

\(=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\\ =\dfrac{2c.2a.2b}{abc}\\ =\dfrac{8abc}{abc}\\ =8\)

TH2:a+b+c=0

\(\Rightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\c+a=-b\end{matrix}\right.\)

\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{-c.-a.-b}{abc}=\dfrac{-abc}{abc}=-1\)

\(5^x=y^2+y+1\)

\(5^x-1=y\left(y+1\right)\)

Với x khác 1

\(\left(....5\right)-1=y\left(y+1\right)\)

\(\left(...4\right)=y\left(y+1\right)\)

Ta thấy các số liên tiếp ko có tận cùng bằng 4

Nên ko có x,y

Với x=1

=> \(1-1=y\left(y+1\right)\)

\(\Rightarrow\hept{\begin{cases}y=0\\y=-1\end{cases}}\)

Mà y là số tự nhiên nên y = 0

Vậy x = 1 ; y = 0

Nên