Bài 1:
Nếu $a+b+c=0$ thì đkđb thỏa mãn
$M=\frac{(-c)(-a)(-b)}{abc}=\frac{-(abc)}{abc}=-1$
Nếu $a+b+c\neq 0$. Áp dụng TCDTSBN:
$\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{c+b+a}=\frac{a+b+c}{a+b+c}=1$
$\Rightarrow a+b-c=c; a+c-b=b; b+c-a=a$
$\Leftrightarrow a+b=2c; a+c=2b; b+c=2a$
$\Rightarrow a=b=c$
$M=\frac{(a+a)(a+a)(a+a)}{aaa}=\frac{8a^3}{a^3}=8$
Bài 2a
Đặt $2x=3y=4z=t$
$\Rightarrow x=\frac{t}{2}; y=\frac{t}{3}; z=\frac{t}{4}$
Khi đó:
$|x+y+3z|=1$
$\Leftrightarrow |\frac{t}{2}+\frac{t}{3}+\frac{3t}{4}|=1$
$\Leftrightarrow |\frac{19}{12}t|=1$
$\Rightarrow t=\pm \frac{12}{19}$
Nếu $t=\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{6}{19}; y=\frac{4}{19}; z=\frac{3}{19}$
Nếu $t=-\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{-6}{19}; y=\frac{-4}{19}; z=\frac{-3}{19}$
Bài 2b:
$\frac{x^3}{8}=\frac{y^3}{27}=\frac{z^3}{64}$
$\Leftrightarrow (\frac{x}{2})^3=(\frac{y}{3})^3=(\frac{z}{4})^3$
$\Leftrightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+2y^2-3z^2=-650$
$\Leftrightarrow (2t)^2+2.(3t)^2-3(4t)^2=-650$
$\Leftrightarrow -26t^2=-650$
$\Leftrightarrow t=\pm 5$
Nếu $t=5$ thì:
$x=2t=10; y=3t=15; z=4t=20$
Nếu $t=-5$ thì:
$x=2t=-10; y=3t=-15; z=4t=-20$
Bài 3:
Nếu $x\geq 5$ thì:
$|x^2-9|+|x^2-25|=26$
$\Rightarrow x^2-9+x^2-25=26$
$\Leftrightarrow 2x^2=60$
$\Leftrightarrow x^2=30$
$\Rightarrow x=\sqrt{30}$ (thỏa mãn)
Nếu $3\leq x< 5$ thì:
$|x^2-9|+|x^2-25|=26$
$\Leftrightarrow x^2-9+25-x^2=26$
$\Leftrightarrow 16=26$ (vô lý)
Nếu $-3\leq x< 3$ thì:
$|x^2-9|+|x^2-25|=26$
$\Leftrightarrow 9-x^2+25-x^2=26$
$\Leftrightarrow x^2=4\Rightarrow x=\pm 2$ (tm)
Nếu $-5\leq x< -3$ thì:
$|x^2-9|+|x^2-25|=26$
$\Leftrightarrow x^2-9+25-x^2=26$
$\Leftrightarrow 16=26$ (vô lý)
Nếu $x< -5$ thì:
$|x^2-9|+|x^2-25|=26$
$\Leftrightarrow x^2-9+x^2-25=26$
$\Leftrightarrow x=-\sqrt{30}$


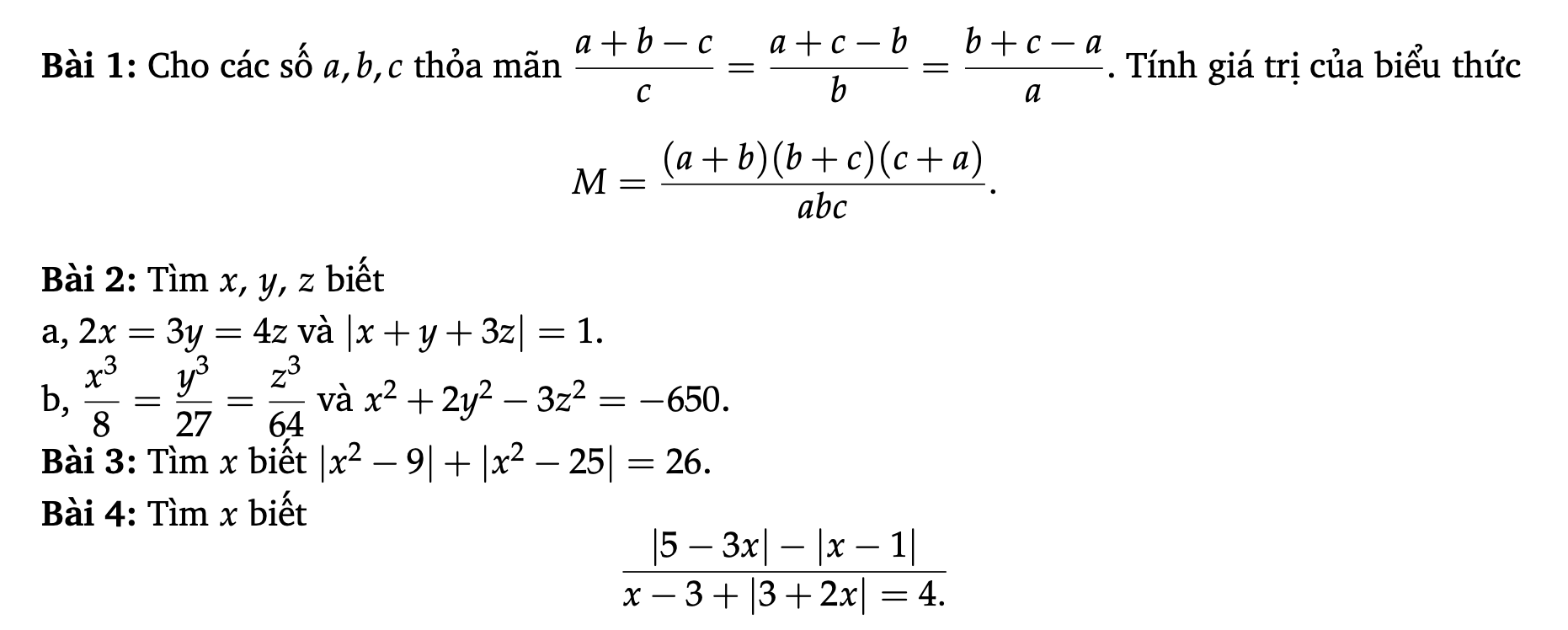


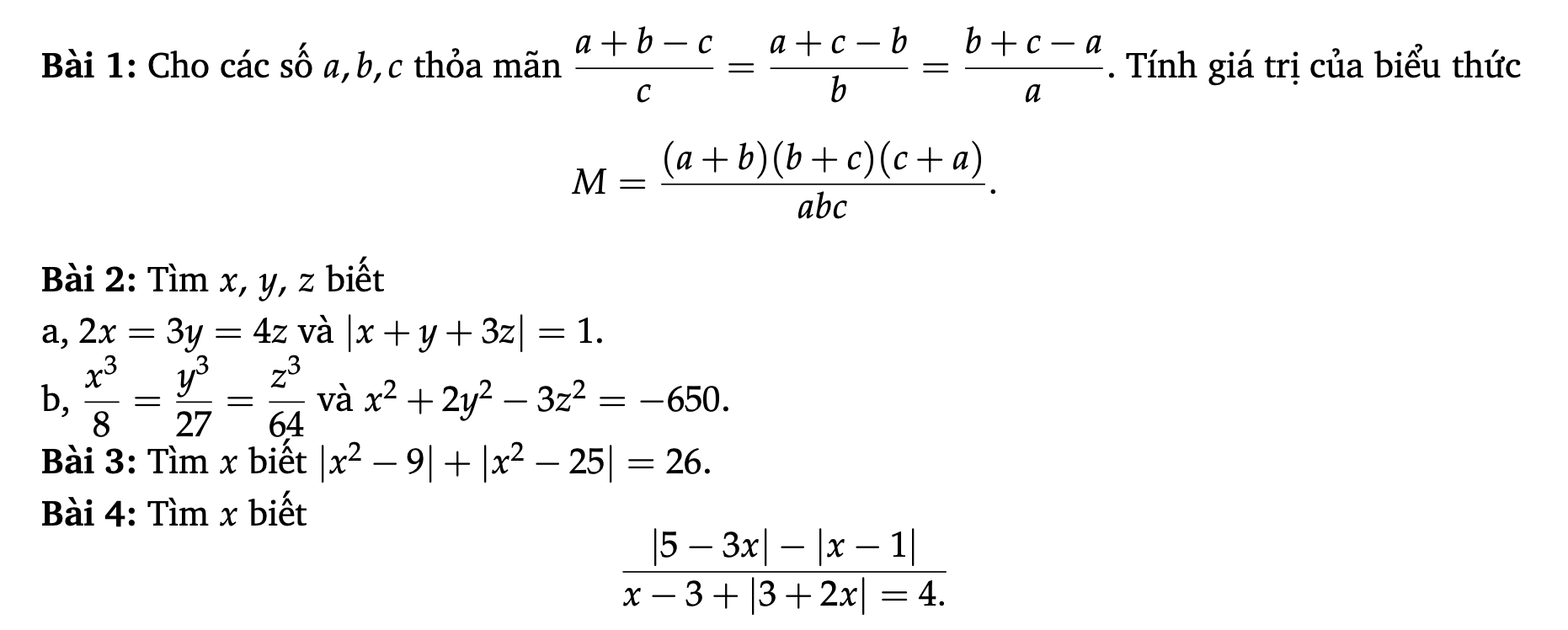
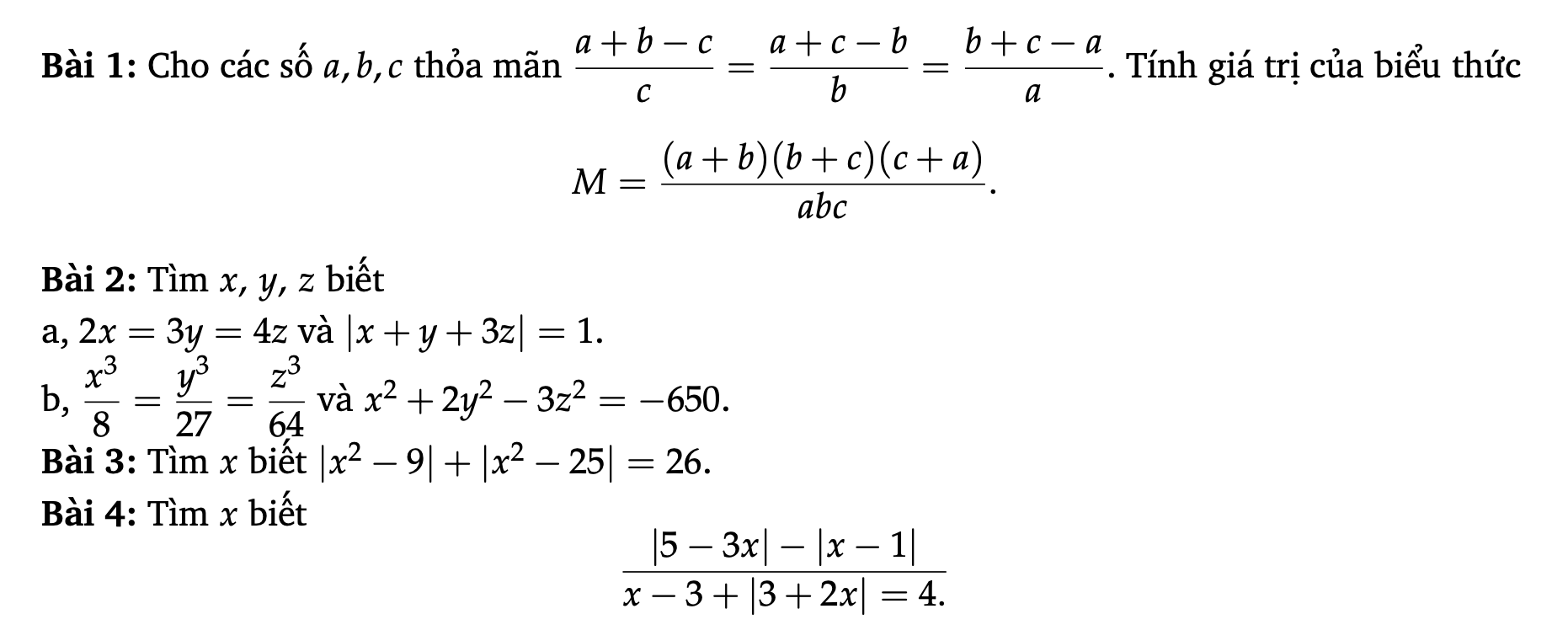
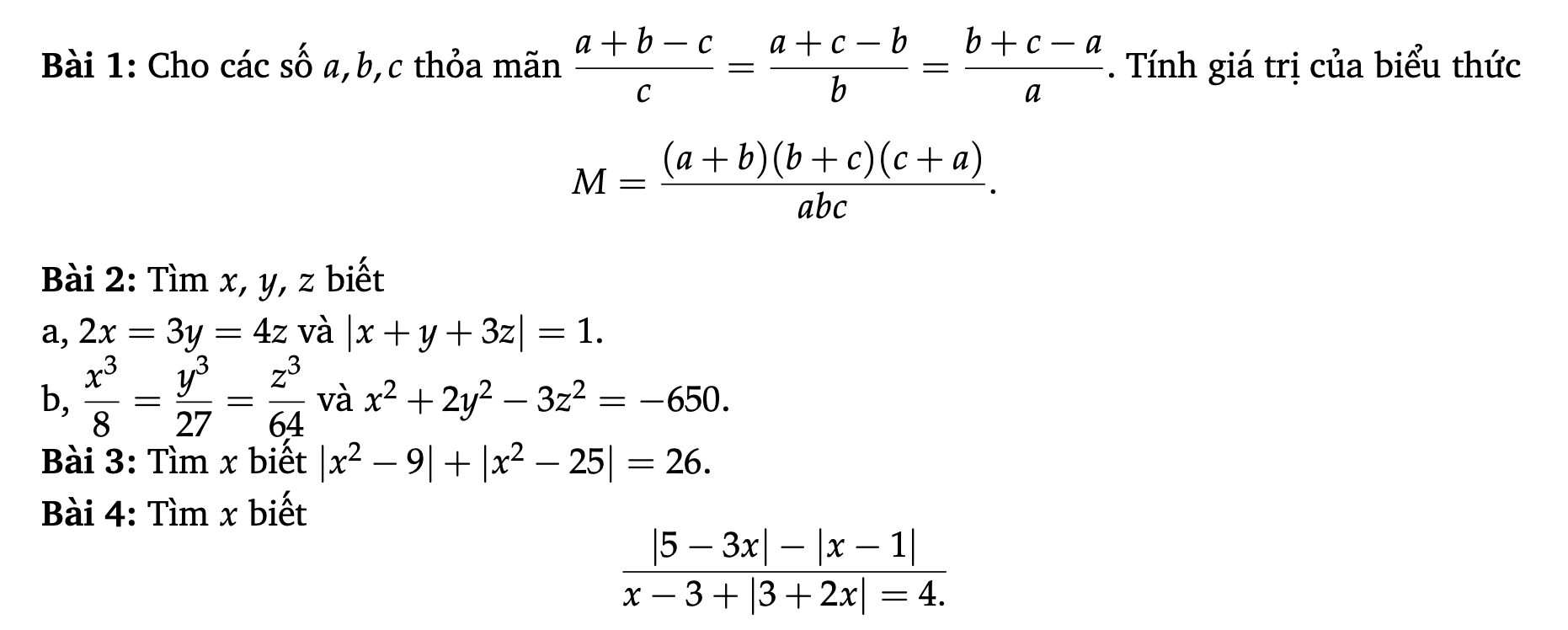


 Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔
Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔

