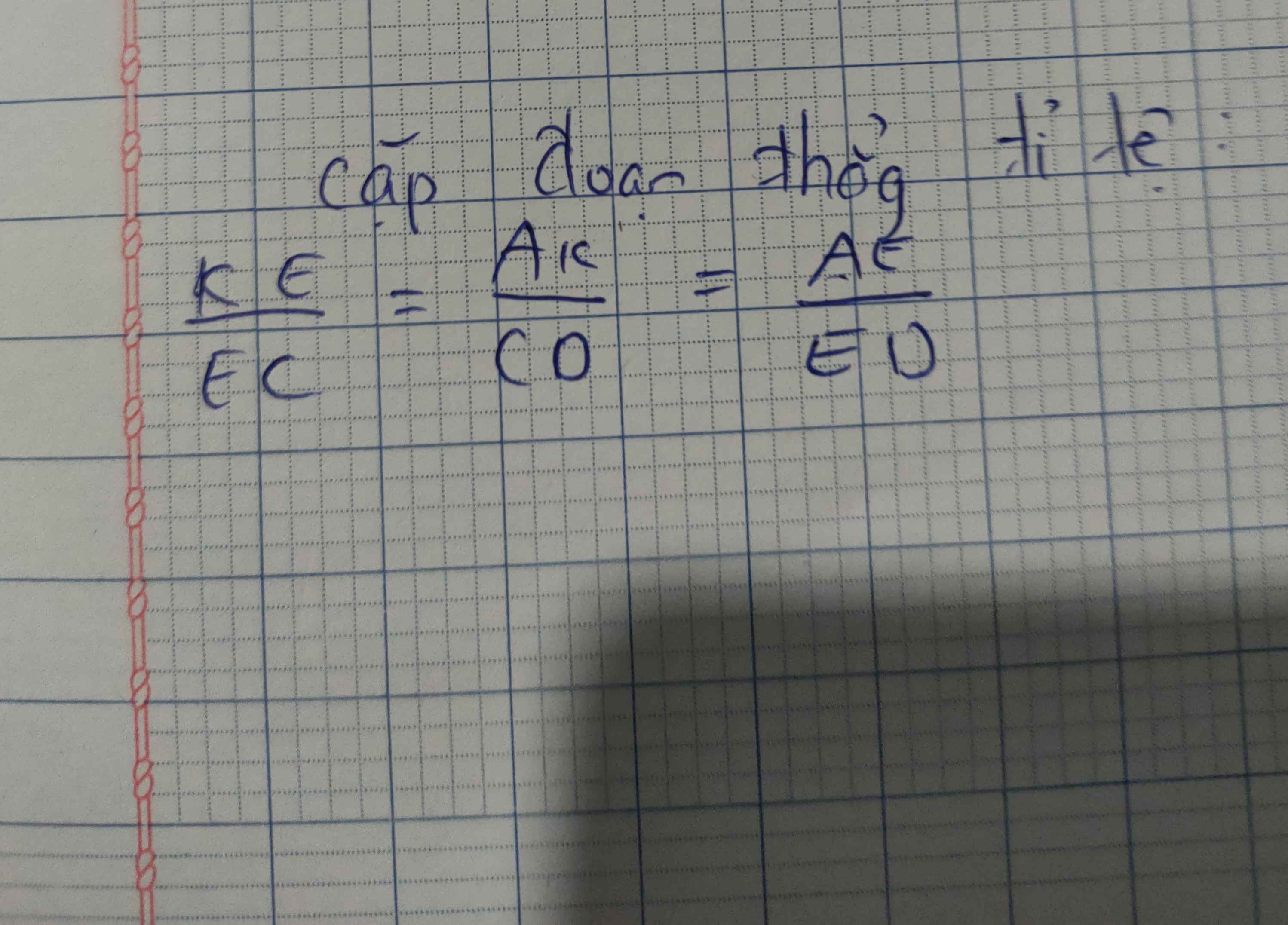giải bài tập này sử dụng định lý thales
giải bài tập này sử dụng định lý thales

Những câu hỏi liên quan
Chứng minh bài toán sau:
Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy cùng nằm trên một đường thẳng.
Vì mình chưa học tam giác đồng dạng nên các bạn giải bằng cách sử dụng điịnh lý Thales
Vẽ hình thang ABCD (AB//CD), giao điểm của AD và BC là E, giao điểm của AC và BD là O; M, N lần lượt là trung điểm của AB và DC.
Ta cần chứng minh E, M, O, N cùng thuộc một đường thẳng.
Gọi N' là giao điểm của EM với DC.
Do AB// CD nên áp dụng định lý Ta let cho các tam giác EDN' và EN'C , ta có:
\(\frac{AM}{DN'}=\frac{EM}{EN'}=\frac{BM}{N'C}\)
Lại có AM = BM nên DN' = N'C hay N' là trung điểm DC.
Suy ra N' trùng N hay E, M, N thẳng hàng.
Gọi N'' là giao điểm của MO với CD.
Do AB// CD nên áp dụng hệ quả định lý Ta let, ta có :
\(\frac{AM}{N''C}=\frac{MO}{ON''}=\frac{MB}{DN''}\)
\(\Rightarrow N''C=DN''\) hay N'' trùng N.
Vậy nên E, M, O, N thẳng hàng.
Đúng 0
Bình luận (0)
Lich sử : Giải bài tập lịch sử lớp 5 bài nước nhà bị chia cắt .
Địa lý : Giải bài tập địa lý lớp 5 bài 18 : Châu Á ( tiếp theo ).
bn có thể tham khảo các link này nhe s
lịch sử https://vndoc.com/giai-vo-bai-tap-lich-su-5-bai-19-nuoc-nha-bi-chia-cat-161254
địa lý https://vndoc.com/giai-vo-bai-tap-dia-ly-5-bai-18-chau-a-tiep-theo-160007
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
hãy nêu các hệ quả của định lý Thales
Refer
Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
Đúng 2
Bình luận (0)
bn tham khảo
Hệ quả 1
Hệ quả 1 của định lý Thales được phát biểu như sau: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho.
Hệ quả 2 của Thales[sửa | sửa mã nguồn]
Hệ quả 2 của định lý Thales được phát biểu như sau: Có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác đã cho.
Hệ quả 3 - Thales mở rộng
Thales mở rộng được phát biểu như sau: Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỉ lệ.
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Phát biểu nào dưới đây là định lý Thales trong không gian A. Ba mặt phẳng song song chắn trên hai cát tuyết song song các đoạn thẳng tương ứng tỉ lệ. B. Ba mặt phẳng song song chắn trên hai cát tuyết bất kì các đoạn thẳng tương ứng tỉ lệ C. Ba mặt phẳng song song chắn trên hai cát tuyết song song các đoạn thẳng tương ứng bằng nhau D. Ba mặt phẳng song song chắn trên hai cát tuyết bất kì các đoạn thẳng tương ứng bằng nhau
Đọc tiếp
Phát biểu nào dưới đây là định lý Thales trong không gian
A. Ba mặt phẳng song song chắn trên hai cát tuyết song song các đoạn thẳng tương ứng tỉ lệ.
B. Ba mặt phẳng song song chắn trên hai cát tuyết bất kì các đoạn thẳng tương ứng tỉ lệ
C. Ba mặt phẳng song song chắn trên hai cát tuyết song song các đoạn thẳng tương ứng bằng nhau
D. Ba mặt phẳng song song chắn trên hai cát tuyết bất kì các đoạn thẳng tương ứng bằng nhau
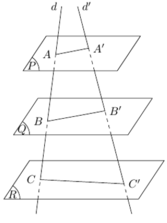
Đáp án B
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
Đúng 0
Bình luận (0)
Chứng minh định lý Ceva và Menelaus theo phương pháp Thales ?
Có trong nâng cao phát triển toán 8 tập 2 nha bạn!!
Ngại viết vì khá là dài :((
* Định lí Menelaus: Cho tam giác ABC, một đường thẳng d không đi qua các đỉnh tam giác, cắt các đường thẳng BC,AC,AB lần lượt tại A', B', C'. Khi đó: \(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=1\)
Cm: Kẻ AH,BK,CN cùng vuông góc với đường thẳng d. Suy ra AH// BK// CN
Theo định lý Ta-lét, ta có: \(\frac{B'A}{B'C}=\frac{AH}{CN};\frac{A'C}{A'B}=\frac{CN}{BK};\frac{C'B}{C'A}=\frac{BK}{AH}\)
Do đó: \(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=\frac{AH}{CN}.\frac{CN}{BK}.\frac{BK}{AH}=1\)(ĐPCM)
* Định lý Ceva: Cho tam giác ABC. Các điểm A',B',C' theo thứ tự thuộc các cạnh BC,AC,AB sao cho AA', BB', CC' đồng quy ở O. Khi đó: \(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=1\)
Cm: Qua A vẽ đường thẳng song song với BC, cắt CC', BB' theo thứ tự tại M,N
Theo định lý Ta-let, ta có:
\(\frac{B'A}{B'C}=\frac{AN}{BC}\)(1)
\(\frac{C'B}{C'A}=\frac{BC}{AM}\)(2)
Cũng theo ta-let, ta có: \(\frac{CA'}{MA}=\frac{OA'}{OA}=\frac{A'B}{AN}\)nên \(\frac{CA'}{A'B}=\frac{MA}{AN}\)(3)
Nhân các đẳng thức (1), (2), (3) theo từng vế, ta được:
\(\frac{B'A}{B'C}.\frac{A'C}{A'B}.\frac{C'B}{C'A}=\frac{AN}{BC}.\frac{MA}{AN}.\frac{BC}{AM}=1\)(ĐPCM)
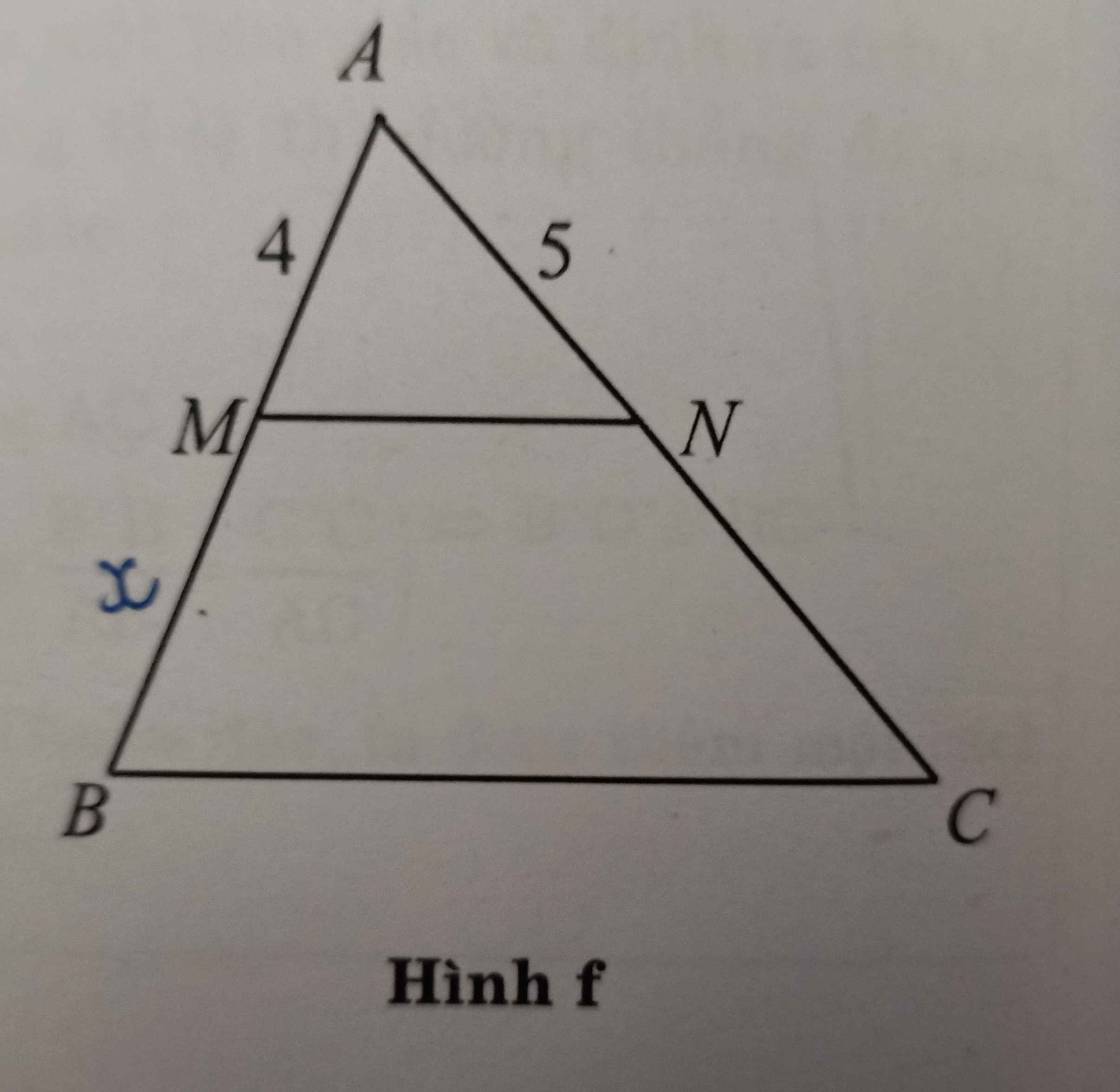
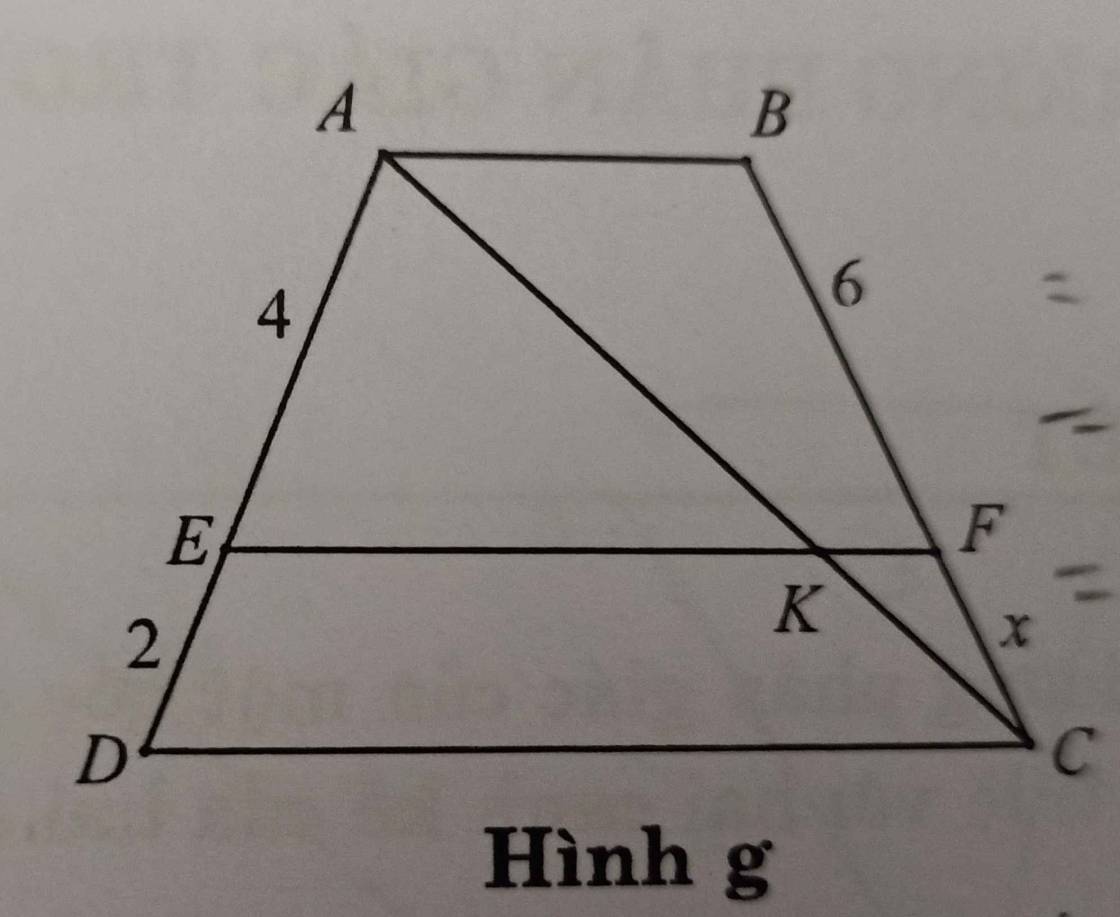 giúp e vs ạ, đề là Tính độ dài của x dùng định lý THALES ý ạ
giúp e vs ạ, đề là Tính độ dài của x dùng định lý THALES ý ạ
Hình f đề bài thiếu nên không tính được
Với hình g:
Áp dụng định lý Talet cho tam giác ADC:
\(\dfrac{AE}{ED}=\dfrac{AK}{KC}\Rightarrow\dfrac{AK}{KC}=\dfrac{4}{2}=2\)
\(\Rightarrow\dfrac{CK}{AK}=\dfrac{1}{2}\)
Áp dụng định lý Talet cho tam giác CAB:
\(\dfrac{CF}{BF}=\dfrac{CK}{AK}\Rightarrow\dfrac{x}{6}=\dfrac{1}{2}\Rightarrow x=3\)
Đúng 1
Bình luận (1)
1/ xác định những câu sau, câu nào sử dụng trợ từ, câu nào không sử dụng trợ từa) Chính tôi là người làm bài tập này.b) Hôm nay tôi làm được những 2 bài tập.c) Đich đến của mọi người là gì?d) Bạn phải làm bài tập này ngay nếu không muốn quên.e) Nhân vật chính của bộ phim không được nổi tiếng lắm.f) Đích thân tôi phải giải quyết mọi việc.2/ Viết đoạn văn có nội dung thời tiết của những ngày tháng 10 có sử dụng thán từ và trợ từ. ( có xác định )
Đọc tiếp
1/ xác định những câu sau, câu nào sử dụng trợ từ, câu nào không sử dụng trợ từ
a) Chính tôi là người làm bài tập này.
b) Hôm nay tôi làm được những 2 bài tập.
c) Đich đến của mọi người là gì?
d) Bạn phải làm bài tập này ngay nếu không muốn quên.
e) Nhân vật chính của bộ phim không được nổi tiếng lắm.
f) Đích thân tôi phải giải quyết mọi việc.
2/ Viết đoạn văn có nội dung " thời tiết của những ngày tháng 10 " có sử dụng thán từ và trợ từ. ( có xác định )

 ai giải hộ em bài này với
ai giải hộ em bài này với
Câu 1: Khi đi trên sàn đá hoa mới lau dễ bị ngã vì lực ma sát nghỉ giữa sàn vơi chân người rất nhỏ => Ma sát trong hiện tượng này có ích.
Câu 2: *Mình nghĩ đề phải đi trên cùng 1 đường và bắt đầu cùng 1 thời gian thì mới làm được*
a) Người thứ 2 đi nhanh hơn do Vận tốc của người thứ 2 nhanh hơn Vận tốc của người thứ nhất.
b)

Gọi A là điểm xuất phát của người 2, B là điểm xuất phát của người thứ 1. C là điểm gặp của 2 người.
\(V_1;V_2\) lần lượt vận tốc của người thứ nhất và người thứ 2.
t là thời gian đi của 2 xe.
Ta có: \(S_{AC}-S_{AB}=17\Rightarrow V_2.t-V_1t=17\Rightarrow60t-40t=20t=17\Rightarrow t=0,86\left(h\right)\)
Câu 3:

Diễn tả bằng lời:
\(\overrightarrow{P}\) là trọng lương của vật đặt tại tâm của vật, phương thẳng đứng chiều từ trên xuống.
\(\overrightarrow{F}\) được đặt tại tâm của vật, phương thẳng đứng chiều từ dưới lên.
Câu 4: Tóm tắt
\(t_1=\frac{1}{3}t\)
\(V_1=12m\)/\(s\)
\(t_2=\frac{2}{3}t\)
\(V_2=9m\)/\(s\)
_________
\(V_{TB}\)=?
Gỉai
Gọi \(S_1;S_2\) lần lượt là quãng đường đi với vận tốc 12km/h; 9 km/h
Ta có công thức sau: \(V_{TB}=\frac{S_1+S_2}{t_1+t_1}\)
Trong đó: \(S_1=V_1.t_1=12.\frac{1}{3}t=4t;S_2=V_2.t_2=9.\frac{2}{3}t=6t\)
\(\Rightarrow V_{TB}=\frac{4t+6t}{t}=10\) ( m/s)
Đúng 0
Bình luận (0)
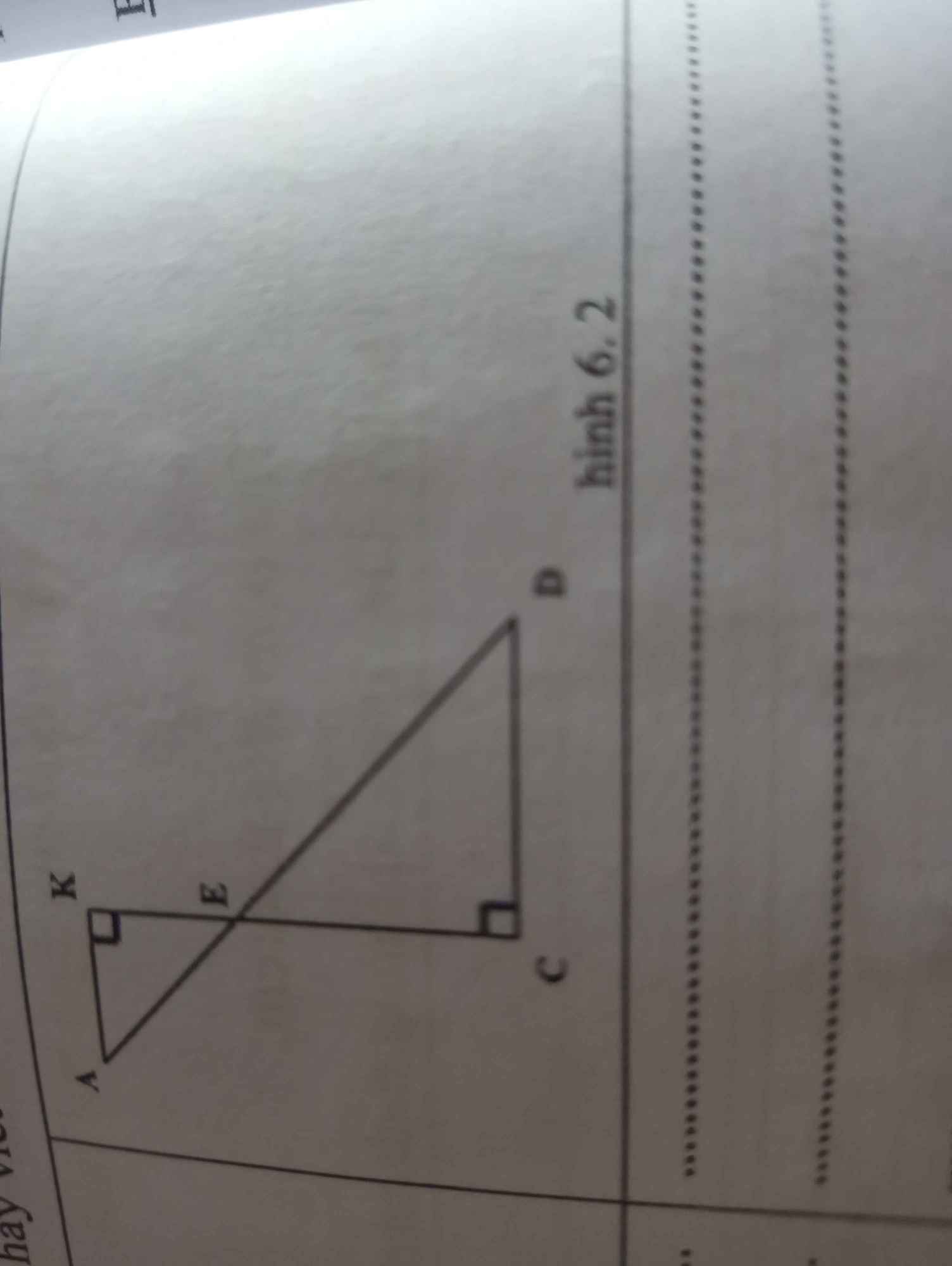
sử dụng hệ quả Thales hãy viết các cặp đoạn thẳng tỉ lệ với các hình sau