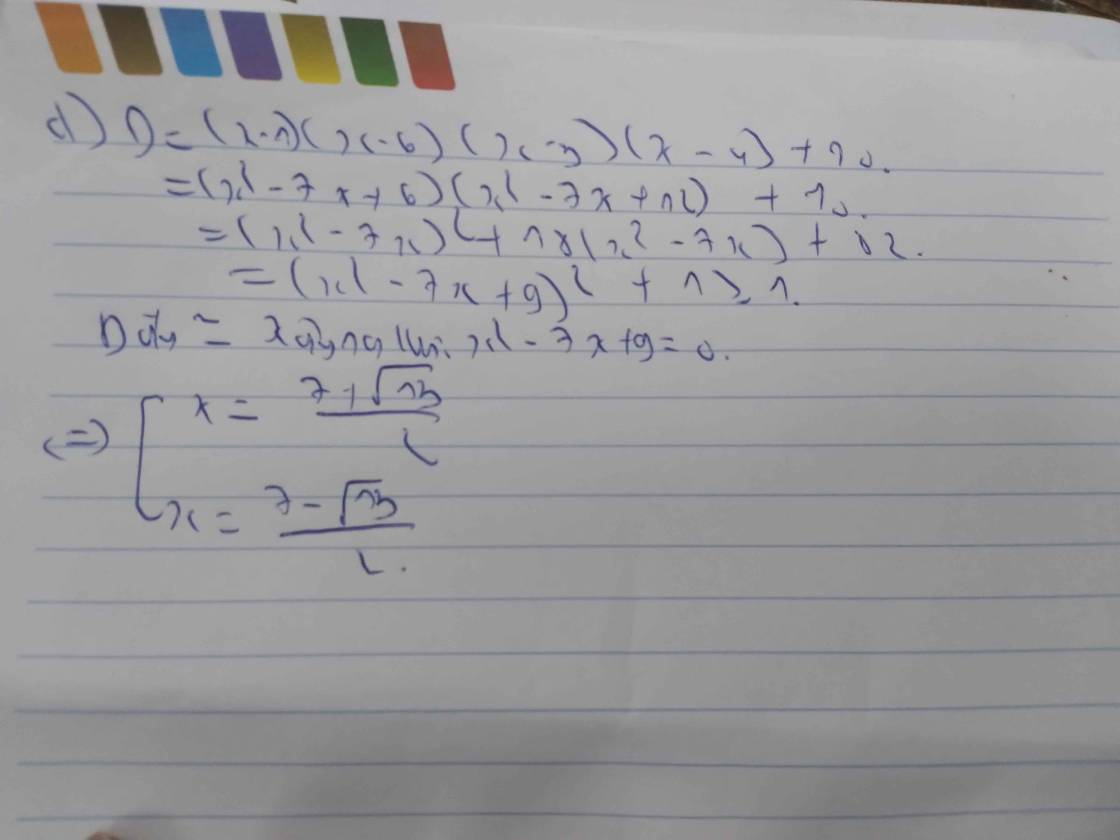a)Ta có:

\(A=4-x^2+2x=-\left(x^2-2x-4\right)=-\left(x^2-2x+1+3\right)\)

\(=-\left(x^2-2x+1\right)-3=-\left(x-1\right)^2-3\le-3\forall x\)

Vậy Max_A=-3 khi x=1

b) Ta có: \(B=4x-x^2=-\left(x^2-4x\right)=-\left(x^2-4x+4-4\right)=-\left(x-2\right)^2+4\le4\forall x\)Vậy Max_B=4 khi x=2

Bài 3: Tìm GTLN

a) Ta có: \(A=4-x^2+2x\)

\(=-\left(x^2-2x-4\right)\)

\(=-\left(x^2-2x+1-5\right)\)

\(=-\left(x-1\right)^2+5\)

Ta có: \(\left(x-1\right)^2\ge0\forall x\)

\(\Rightarrow-\left(x-1\right)^2\le0\forall x\)

\(\Rightarrow-\left(x-1\right)^2+5\le5\forall x\)

Dấu '=' xảy ra khi x-1=0

hay x=1

Vậy: GTLN của biểu thức \(A=4-x^2+2x\) là 5 khi x=1

b) Ta có: \(B=4x-x^2\)

\(=-\left(x^2-4x\right)\)

\(=-\left(x^2-4x+4-4\right)\)

\(=-\left(x-2\right)^2+4\)

Ta có: \(\left(x-2\right)^2\ge0\forall x\)

\(\Rightarrow-\left(x-2\right)^2\le0\forall x\)

\(\Rightarrow-\left(x-2\right)^2+4\le4\forall x\)

Dấu '=' xảy ra khi x-2=0

hay x=2

Vậy: GTLN của biểu thức \(B=4x-x^2\) là 4 khi x=2

a: \(B=1-\sqrt{\left(x-1\right)^2+1}\)

(x-1)^2+1>=1

=>\(\sqrt{\left(x-1\right)^2+1}>=1\)

=>\(B< =0\)

Dấu = xảy ra khi x=1

b: 

ĐKXĐ: -(x+2)^2+2>=0

=>-(x+2)^2>=2

=>(x+2)^2<=2

=>\(-\sqrt{2}-2< =x< =\sqrt{2}-2\)

\(-x^2+4x-2=-\left(x^2-4x+2\right)\)

\(=-\left(x^2-4x+4-2\right)=-\left(x-2\right)^2+2< =2\)

=>\(0< =\sqrt{4x-x^2-2}< =\sqrt{2}\)

=>1<=C<=căn 2+1

\(C_{max}=\sqrt{2}+1\Leftrightarrow x=2\)

Bạn xem lại đề nhé.

a) \(A=x^2+5y^2+2xy-4x-8y+2015\)

\(A=x^2-4x+4-2y\left(x-2\right)+y^2+2011+4y^2\)

\(A=\left(x-2\right)^2-2y\left(x-2\right)+y^2+2011+4y^2\)

\(A=\left(x-2-y\right)^2+4y^2+2011\)

Vì \(\left(x-y-2\right)^2\ge0;4y^2\ge0\)

\(\Rightarrow A_{min}=2011\)

Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-y-2=0\\4y^2=0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

b) \(B=\left(x-2012\right)^2+\left(x+2013\right)^2\)

\(B=x^2-4024x+2012^2+x^2+4026x+2013^2\)

\(B=2x^2+2x+2012^2+2013^2\)

\(B=2\left(x^2+x+\dfrac{1}{4}\right)+2012^2+2013^2-\dfrac{1}{2}\)

\(B=2\left(x+\dfrac{1}{2}\right)^2+2012^2+2013^2-\dfrac{1}{2}\)

\(\Rightarrow B_{min}=2012^2+2013^2-\dfrac{1}{2}\)

Dấu bằng xảy ra : \(\Leftrightarrow x=-\dfrac{1}{2}\)

\(A=4-6x-x^2=-\left(x^2+6x-4\right)=-\left(x^2+6x+9-13\right)\)

\(=-\left[\left(x+3\right)^2-13\right]=-\left(x+3\right)^2+13\le13\)

Vậy \(A_{max}=13\Leftrightarrow x+3=0\Leftrightarrow x=-3\)

\(B=3x^2-6x+1=\left(\sqrt{3}x\right)^2-2.\sqrt{3}x.\sqrt{3}+3-2\)

\(=\left(\sqrt{3}x-\sqrt{3}\right)^2-2\ge-2\)

Vậy \(B_{min}=-2\Leftrightarrow\sqrt{3}x-\sqrt{3}=0\Leftrightarrow x=1\)

\(C=5x^2-2x-3=\left(\sqrt{5}x\right)^2-2.\sqrt{5}x.\frac{1}{\sqrt{5}}+\frac{1}{5}-\frac{16}{5}\)

\(=\left(\sqrt{5}x-\frac{1}{\sqrt{5}}\right)^2-\frac{16}{5}\ge-\frac{16}{5}\)

Vậy \(C_{min}=-\frac{16}{5}\Leftrightarrow\sqrt{5}x-\frac{1}{\sqrt{5}}=0\Leftrightarrow\sqrt{5}x=\frac{1}{\sqrt{5}}\Leftrightarrow x=\frac{1}{5}\)

a, Ta có :

 \(M=4\left|x+3\right|\ge0\) với \(\forall x\)

\(\Rightarrow7-4\left|x+3\right|\le7 với \forall x\)

Dấu '' = '' xảy ra khi:

 \(\left|x+3\right|=0\\ \Rightarrow x+3=0\\ \Rightarrow x=-3\)

    Vậy GTLN của \(M=7-4\left|x+3\right|\) là  khi \(x=-3\)

b,

Để \(N=\dfrac{18}{\left|x-2\right|+9}+5\) có giá trị lớn nhất thì \(\dfrac{18}{\left|x-2\right|+9}\) phải lớn nhất

\(\Rightarrow\left|x-2\right|+9\) Phải nhỏ nhất và lớn hơn 0

Ta có:

\(\left|x-2\right|\ge0 với \forall x\)

\(\Rightarrow\left|x-2\right|+9\ge0 với \forall x\)

  Dấu '' = '' xảy ra khi:

\(\left|x-2\right|=0\\ \Rightarrow x-2=0\\ \Rightarrow x=2\) 

\(\Rightarrow\dfrac{18}{\left|x-2\right|+9}+5=2+5=7\)

    Vậy GTLN của \(N=\dfrac{18}{\left|x-2\right|+9}+5\) là 7 khi \(x=2\)