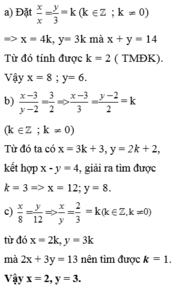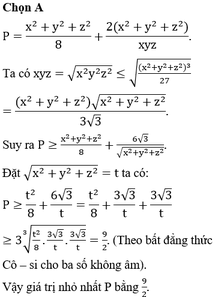tìm y:(y:3)x8=8x3198

Những câu hỏi liên quan
tìm y biết:(y:3)x8=8x3198
đao hả tự nhiên bỏ giấy một mớ thôi
Đúng 0
Bình luận (0)
[ y : 3 ] x 8=25584
y : 3 =25584 : 8
y : 3 =3198
y = 3198 x3
y = 9594
Đúng 0
Bình luận (0)
Bài 1 tìm y
a) (1/2x4+1/4x6+1/6x8+1/8x10)x y =1/3
b) y:8+y x8-56,78=69,11x2
Bài 1.Tính giá trị biểu thức:
a) A = a(b+3)-b(3+b tại a=2003;b=1997
b) C = xy(x+y)-2x-2y tại xy=8;x+y=7
Bài 2.Tìm x, biết:
a) x4-16x2=0 b) x8+36x4=0
Bài 2:
a: \(x^2\left(x^2-16\right)=0\)
\(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
b: \(x^8+36x^4=0\)
\(\Leftrightarrow x^4=0\)
hay x=0
Đúng 1
Bình luận (0)
a(b+3)-b(3+b)
=(3+b)(a-b)
Thay số, có: (3+1997).(2003-1997)
= 2000.6 =12000
xy(x+y)-2x-2y
xy(x+y)- 2(x+y)
(x+y).(xy-2)
Thay số, co: 7. (8-2)
7.4=28
Đúng 1
Bình luận (0)
Tìm các số nguyên x, y, biết:a)
x
4
y
3
và x + y 14b)
x
−
3
y
−
2
3
2
và x - y 4c)
x
8
y
12
và 2x + 3y 13
Đọc tiếp
Tìm các số nguyên x, y, biết:
a) x 4 = y 3 và x + y = 14
b) x − 3 y − 2 = 3 2 và x - y = 4
c) x 8 = y 12 và 2x + 3y = 13
Tìm các số tự nhiên x và y, biết
a) x 8 = 1 y
b) 2 x = x 18 và x < 0
Cho x,y,z là ba số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức P
x
(
x
8
+
2
yz
)
+
y
(
y
8
+
2
xz
)
+
z
(
z
8
+
2
xy
)
. A. 9/2...
Đọc tiếp
Cho x,y,z là ba số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức P= x ( x 8 + 2 yz ) + y ( y 8 + 2 xz ) + z ( z 8 + 2 xy ) .
A. 9/2.
B. 9/4.
C.9.
D. 6.
Tìm x và y biết rằng x8=y9x8=y9 , x2−y2=−68x2−y2=−68 , x và y là những số dương.
Cho x 8 = y - 7 = z 12 và 3x + 10y - 2z = 236. Tính x + y + z
A. -26
B. 26
C. -22
D. 6
Rút gọn biểu thức:
x(x + y)(x2+y2)(x4+y4)(x8+y8)(x - y) + xy16
\(x\left(x+y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)\left(x-y\right)+xy^{16}\\ =x\left(x+y\right)\left(x-y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\\ =x\left(x^2-y^2\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\\ =x\left(x^4-y^4\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\\ =x\left(x^8-y^8\right)\left(x^8+y^8\right)+xy^{16}\\ =x\left(x^{16}-y^{16}\right)+xy^{16}\\ =x^{17}-xy^{16}+xy^{16}\\ =x^{17}\)
Đúng 1
Bình luận (0)
\(x\left(x+y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)\left(x-y\right)+xy^{16}\)
\(=x\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\)
\(=x\left(x^2-y^2\right)\left(x^2+y^2\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\)
\(=x\left(x^4-y^4\right)\left(x^4+y^4\right)\left(x^8+y^8\right)+xy^{16}\)
\(=x\left(x^8-y^8\right)\left(x^8+y^8\right)+xy^{16}\)
\(=x\left(x^{16}-y^{16}\right)+xy^{16}\)
\(=x^{17}-xy^{16}+xy^{16}\)
\(=x^{17}\)
Đúng 1
Bình luận (0)
\(x(x+y)(x^2+y^2)(x^4+y^4)(x^8+y^8)(x-y)+xy^{16}\\=x(x-y)(x+y)(x^2+y^2)(x^4+y^4)(x^8+y^8)+xy^{16}\\=x(x^2-y^2)(x^2+y^2)(x^4+y^4)(x^8+y^8)+xy^{16}\\=x(x^4-y^4)(x^4+y^4)(x^8+y^8)+xy^{16}\\=x(x^8-y^8)(x^8+y^8)+xy^{16}\\=x(x^{16}-y^{16})+xy^{16}\\=x^{17}-xy^{16}+xy^{16}\\=x^{17}\\Toru\)
Đúng 0
Bình luận (0)